3.3. Словарь терминов раздел «Основные понятия и методы математического анализа (функции, последовательности, пределы, производные)»

Функциональные понятия.

Функция. Пустьимножества, если каждому значению по определенному законуставится в соответствие одно определенное значение переменной, то говорят, чтоесть однозначная функция от, и обозначают.

Область определения, область значения функции.МножествоD(у)на котором функцияимеет смысл называется областью определения функции, а множествоЕ(у)- значения всех- область значения функции.

Способы задания функции.Аналитический – с помощью формулы, графический, табличный.

Элементарная функция. Функцияназывается элементарной, если она является одной из основных элементарных функций или комбинацией элементарных функций (целая рациональная, дробно-рациональная, иррациональная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, сложная).

Числовая последовательность. Бесконечной числовой последовательностью называется функция, определенная на множестве натуральных чисел,- члены числовой последовательности.

Предел числовой последовательности. Числоназывается пределом числовой последовательности, если для любого сколь угодно малого числанайдется такой номер, зависящий от, что для любоговыполняется неравенство, обозначается.

Предел функции. Числоназывается пределом функциипри, если для любого сколь угодно малого числанайдется такое, зависящее от, что для любого, как только, выполняется неравенство, обозначается.

Бесконечно малые. Функцияназывается бесконечно малой при, если для любого сколь угодно малого числанайдется такое, зависящее от, что для любого, как только, выполняется неравенство, обозначается.

Бесконечно большие. Функцияназывается бесконечно большой при, если для любого числанайдется такое, зависящее от, что для любого, как только, выполняется неравенство, обозначается.

Свойства бесконечно малых и бесконечно больших.Пусть- бесконечно малые функции при,- бесконечно большие функции при,- ограниченная функция при,- постоянная при, тогда:

1. - бесконечно малая функция;

2. - бесконечно малая функция;

3. - бесконечно малая функция;

4. - бесконечно малая функция;

5. - бесконечно большая функция;

6.- бесконечно большая функция;

7. - бесконечно малая функция.

Основные теоремы о пределах.

Теорема 1.Для того, чтобы числобыло пределом функциинеобходимо и достаточно, чтобы эта функция была представлена в виде, где- бесконечно малая функция.

Теорема 2., если- постоянная при.

Теорема 3. Если() в окрестности точки, то().

Теорема 4.Если существуети, тогда:

=+;

=;

;

(;

.

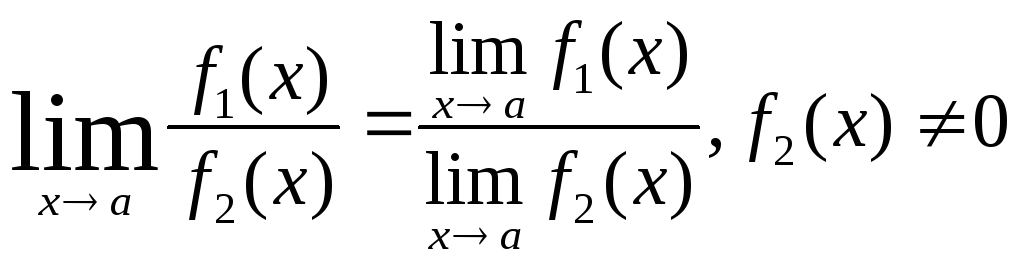Теорема 5.Если существуети, функцияудовлетворяет условию, то.

Первый замечательный предел, следствия.

.

Следствия: ,,.

Второй замечательный предел, следствия.

.

Следствия: ,,.

Понятие непрерывности функции в точке. Пусть функцияопределена в интервале,- произвольные значения аргумента из. Функцияназывается непрерывной в точке, тогда и только тогда, когда.

Понятие непрерывности функции на сегменте. Функцияназывается непрерывной на сегменте тогда и только тогда, когда функциянепрерывна в каждой точке сегмента.

Свойства функций, непрерывных на сегменте.

1. Если функция непрерывна на сегменте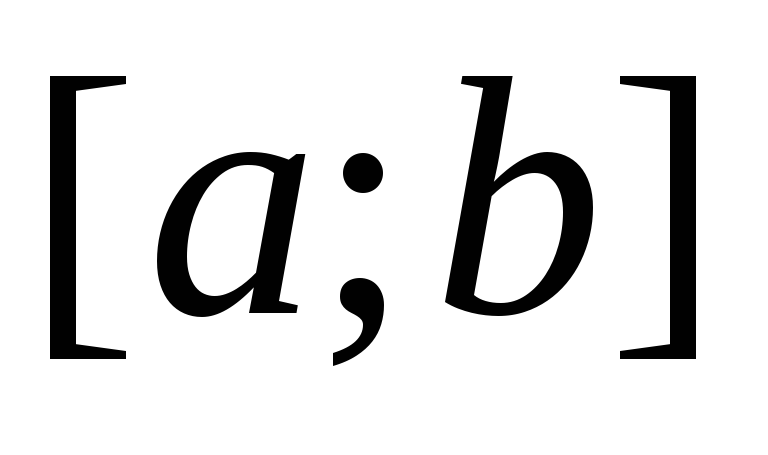и,разных знаков, то существует, что.

2. Если функция непрерывна на сегменте, то она ограничена на.

3. Если функция непрерывна на сегменте, то существуют, такие, что- наибольшее значение функции,- наименьшее значение функции.

Точки разрыва.Пусть функцияопределена в интервале, кроме, может быть, точки, иили не существует, то точканазывается точкой разрыва.

Производная функции. Производной функции f(х) в точке х₀ Î (a,b) называется предел , если он существует, то функция называется дифференцируемой в точке х₀.

Правила дифференцирования.Пусть- дифференцируемые, т.е. производныесуществуют, тогда:

;

;

, - постоянная;

;

, где ;

, где,- взаимообратные функции;

, - постоянна.

Производные элементарных функций.

;

;

;

;

;

;

;

;

;

;

;

;

.

Дифференциал функции. Если f(х) дифференцируема в точке х₀, то главная линейная часть приращения функцииназывается дифференциалом функции в точке и обозначается:

.

Применение дифференциала к приближенным вычислениям.

- формула приближенных вычислений.