
- •Аксиомы Колмогорова
- •Свойства Вероятностей
- •Действительно , , ,
- •Классическое определение вероятности, условие применимости
- •Геометрическое определение вероятности
- •– Геометрическое определение вероятности
- •Условная вероятность, теорема умножения вероятностей. Независимость случайных событий.
- •Формула полной вероятности, условия применимости
- •Формула Байеса.
- •Локальная предельная теорема Муавра – Лапласа
- •Интегральная предельная теорема
- •Функция распределения случайной величины. Свойства
- •Функция распределения. Ряд распределения дискретной случайной величины
- •Плотность распределения непрерывной случайной величины, свойства
- •Функция распределения, плотность вероятностей многомерной случайной величины. Независимость случайных величин.
- •Математическое ожидание случайной величины. Свойства.
- •Дисперсия случайной величины. Свойства
- •Коэффициент корреляции случайных величин. Свойства
- •Биномиальный закон распределения случайной величины, числовые характеристики
- •Равномерный закон распределения, числовые характеристики
- •Нормальный (гауссовский) закон распределения, числовые характеристики
-
Математическое ожидание случайной величины. Свойства.
Пусть
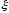 - дискретная
случайная величина с возможными
значениями
- дискретная
случайная величина с возможными
значениями
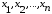 и вероятностями
этих значений
и вероятностями
этих значений
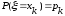 ,
k
= 1,2,…,n.
,
k
= 1,2,…,n.
Определение. Математическим ожиданием дискретной случайной величины называется число
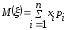 (1)
(1)
Если случайная величина имеет бесконечное число возможных значений, то для существования ее математического ожидания необходима сходимость ряда
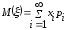 (2)
(2)
Пусть
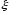 - непрерывная
случайная величина, плотность вероятностей
которой
- непрерывная
случайная величина, плотность вероятностей
которой
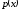
Определение. Математическим ожиданием непрерывной случайной величины называется число
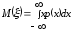 (3)
(3)
Определение.
Математическим
ожиданием функции случайной
величины
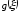 называется число
называется число
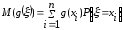 - для дискретной
величины
- для дискретной
величины
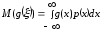 - для непрерывной
величины
- для непрерывной
величины
Определение.
Математическим
ожиданием многомерной случайной
величины
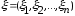 называется вектор
называется вектор
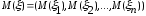 ,
,
где
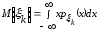 ,
k
= 1,2,…,n
,
k
= 1,2,…,n
или
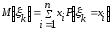 ,
k
= 1,2,…,n
,
k
= 1,2,…,n
Свойства математического ожидания
1.
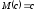 ,
с
= const
,
с
= const
2.
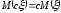 ,
с
= const
,
с
= const
3.
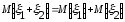
Действительно, для непрерывных случайных величин
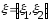 ,
,
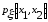
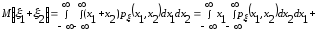
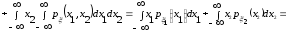
=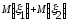
Следствие.
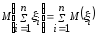
4.
Пусть
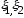 независимы, тогда
независимы, тогда
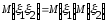
Действительно, для непрерывных случайных величин
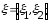 ,
,
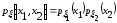

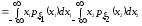 =
=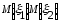
-
Дисперсия случайной величины. Свойства
Пусть случайная
величина
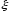 имеет математическое
ожидание
имеет математическое
ожидание
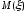 .
.
Определение.
Дисперсией
случайной величины
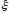 называется число
называется число
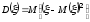 (1)
(1)
Из (1)
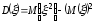 (2)
(2)
Пусть
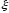 - дискретная
случайная величина с возможными
значениями
- дискретная
случайная величина с возможными
значениями
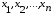 и вероятностями
этих значений
и вероятностями
этих значений
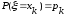 ,
k
= 1,2,…,n.
,
k
= 1,2,…,n.
Тогда
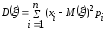 (3)
(3)
Пусть
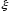 - непрерывная
случайная величина, плотность вероятностей
которой
- непрерывная
случайная величина, плотность вероятностей
которой
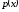 .
Тогда
.
Тогда
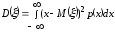 (4)
(4)
Определение.
Средним
квадратическим отклонением
случайной величины
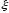 называется число
называется число
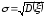
Определение.
Дисперсией
случайной величины
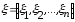 называется матрица
называется матрица
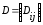 ,
где
,
где
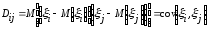 =
=
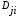

Свойства дисперсии
1.
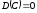 ,
С = const.
,
С = const.
2.
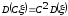
3.
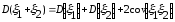 ,
где
,
где
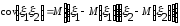
Действительно
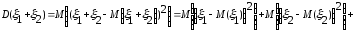
+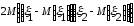 =
=
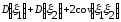 .
.
Следствие.
а) Пусть
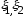 независимы, тогда
независимы, тогда
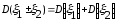
б) Пусть С = const.
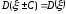
в) Пусть
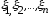 независимы, тогда
независимы, тогда
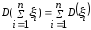
4. Пусть
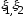 независимы, тогда
независимы, тогда
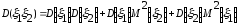
Действительно
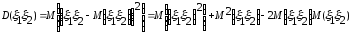 =
=
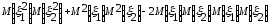 =
=
=
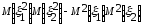
Так как
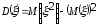 и, следовательно
и, следовательно
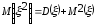 ,
то
,
то
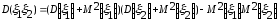 =
=
=
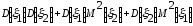
-
Коэффициент корреляции случайных величин. Свойства
Пусть
ξ1,
ξ2
- случайные величины, для которых
существуют
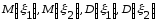
Определение. Коэффициентом корреляции случайных величин ξ1, ξ2 называется число
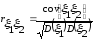 (1)
(1)
где
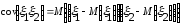 (2)
(2)
Если ξ1, ξ2 дискретные случайные величины и xi – возможные значения величины ξ1, yi - возможные значения величины ξ2, то
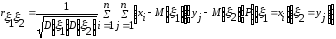 (3)
(3)
Если
ξ1,
ξ2
непрерывные случайные величины и
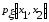 - плотность
вероятностей вектора
- плотность
вероятностей вектора
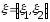 ,
то
,
то
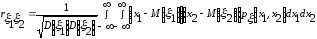 (4)
(4)
Свойства коэффициента корреляции
1.
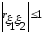
2.
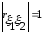 в том и только том
случае, если ξ1,
ξ2
связаны линейной зависимостью
в том и только том
случае, если ξ1,
ξ2
связаны линейной зависимостью
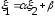 ,
,
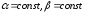 .
.
3. Если ξ1, ξ2 независимы, то
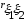 = 0
= 0
Замечание.
Из того, что
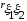 = 0 еще не следует,
что ξ1,
ξ2
независимы.
= 0 еще не следует,
что ξ1,
ξ2
независимы.
