
- •Аксиомы Колмогорова
- •Свойства Вероятностей
- •Действительно , , ,
- •Классическое определение вероятности, условие применимости
- •Геометрическое определение вероятности
- •– Геометрическое определение вероятности
- •Условная вероятность, теорема умножения вероятностей. Независимость случайных событий.
- •Формула полной вероятности, условия применимости
- •Формула Байеса.
- •Локальная предельная теорема Муавра – Лапласа
- •Интегральная предельная теорема
- •Функция распределения случайной величины. Свойства
- •Функция распределения. Ряд распределения дискретной случайной величины
- •Плотность распределения непрерывной случайной величины, свойства
- •Функция распределения, плотность вероятностей многомерной случайной величины. Независимость случайных величин.
- •Математическое ожидание случайной величины. Свойства.
- •Дисперсия случайной величины. Свойства
- •Коэффициент корреляции случайных величин. Свойства
- •Биномиальный закон распределения случайной величины, числовые характеристики
- •Равномерный закон распределения, числовые характеристики
- •Нормальный (гауссовский) закон распределения, числовые характеристики
-
Функция распределения случайной величины. Свойства
Пусть задано
вероятностное пространство
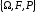 ,
,
 .
.
Определение.
Случайной
величиной
ξ называется такая числовая функция
 ,
что
,
что

 .
.
Свойства функции распределения
1. Монотонность
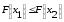 ,
,

Доказательство.
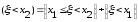

 (2)
(2)
Так как всегда
 ,
то из (2) F(x1)
≤ F(x2).
,
то из (2) F(x1)
≤ F(x2).
2.

3.
 ,
,

Доказательство. Возьмем числовые последовательности
 ,
,
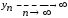
Пусть
 ,
тогда
,
тогда
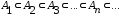
Очевидно
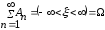
Согласно аксиоме Колмогорова
 (3)
(3)
Или
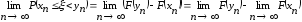 =
=
=
Последнее
справедливо, если
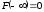 ,
,
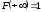 .
.
4. Непрерывность слева.


-
Функция распределения. Ряд распределения дискретной случайной величины
Пусть
 - дискретная
случайная величина с возможными
значениями
- дискретная
случайная величина с возможными
значениями
 и вероятностями
этих значений
и вероятностями
этих значений
 ,
k
= 1,2,…,n.
,
k
= 1,2,…,n.
 (4)
(4)
(4) – условие нормировки вероятностей.
По определению функции распределения

 (5)
(5)
Ряд распределения
|
x1 |
x2 |
… |
xn |
|
p1 |
p2 |
... |
pn |

-
Плотность распределения непрерывной случайной величины, свойства
Определение.
Плотностью распределения
непрерывной случайной величины ξ с
функцией распределения
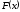 называется такая интегрируемая функция
называется такая интегрируемая функция
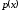 ,
что для любых
,
что для любых
 имеет место
имеет место
 (6)
(6)

Свойства плотности распределения
1.
 ,
,

Действительно

2.

Действительно
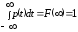
3.

Действительно
Пусть
существует такое В,
что
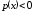 для
для
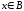
Тогда
 .
Но
.
Но
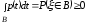 .
.
Полученное противоречие доказывает свойство (3).

-
Функция распределения, плотность вероятностей многомерной случайной величины. Независимость случайных величин.
Пусть на вероятностном пространстве заданы случайные величины
 ,
,
 .
.
Определение. n- мерной случайной величиной называется вектор
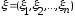
Определение.
Функцией
распределения
случайного вектора
 называется функция
называется функция
 ,
,
 (1)
(1)
-
Монотонность по каждому аргументу.
 ,
,

-
Непрерывность слева по каждому аргументу.
 ,
,

3.

 ,
,

4.


Определение.
Плотностью
распределения (плотностью вероятностей)
случайного вектора
 называется такая
интегрируемая функция
называется такая
интегрируемая функция
 ,
для которой
,
для которой
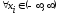 имеет место
имеет место
 (2)
(2)
 (3)
(3)
Свойства плотности вероятностей
1.

2.
 - условие нормировки
- условие нормировки
3.

4.

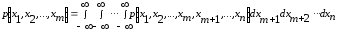
Определение.
Случайные величины
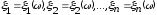 называются независимыми,
если для любых
называются независимыми,
если для любых
 ,
,
 ,
k = 2,3,…, n
,
k = 2,3,…, n
имеет место
 (4)
(4)
В частности из (4)
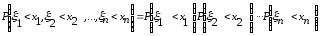
то есть
 (5)
(5)
Из (5)
 (6)
(6)
Следовательно, для независимых случайных величин
 (7)
(7)
Если
 - дискретная
случайная величина и компоненты
- дискретная
случайная величина и компоненты
 независимы, то
независимы, то
 (8)
(8)
