
- •Аксиомы Колмогорова
- •Свойства Вероятностей
- •Действительно , , ,
- •Классическое определение вероятности, условие применимости
- •Геометрическое определение вероятности
- •– Геометрическое определение вероятности
- •Условная вероятность, теорема умножения вероятностей. Независимость случайных событий.
- •Формула полной вероятности, условия применимости
- •Формула Байеса.
- •Локальная предельная теорема Муавра – Лапласа
- •Интегральная предельная теорема
- •Функция распределения случайной величины. Свойства
- •Функция распределения. Ряд распределения дискретной случайной величины
- •Плотность распределения непрерывной случайной величины, свойства
- •Функция распределения, плотность вероятностей многомерной случайной величины. Независимость случайных величин.
- •Математическое ожидание случайной величины. Свойства.
- •Дисперсия случайной величины. Свойства
- •Коэффициент корреляции случайных величин. Свойства
- •Биномиальный закон распределения случайной величины, числовые характеристики
- •Равномерный закон распределения, числовые характеристики
- •Нормальный (гауссовский) закон распределения, числовые характеристики
-
Формула полной вероятности, условия применимости
Пусть случайные
события
 несовместны и образуют полную группу
событий
несовместны и образуют полную группу
событий
 ø,
ø,


 ,
,
 ,
,

Тогда

и
 (1)
(1)
-
– формула полной вероятности.
-
Формула Байеса.

-
Схема испытаний Бернули, формула Бернули
Определение. Схемой испытаний Бернулли называется последовательность n независимых испытаний с двумя исходами 0,1, такая, что для элементов ω пространства элементарных событий Ω имеет место
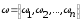 ,
,
 ,
,
 ,
,
 ,
,
где
 - число «1» в векторе
ω.
- число «1» в векторе
ω.
Исход испытания «1» - успех, исход испытания «0» - неудача.
Теорема. Пусть
 - число успехов
в n
испытаниях Бернулли с вероятностью
успеха p.
Тогда
- число успехов
в n
испытаниях Бернулли с вероятностью
успеха p.
Тогда
 ,
m
= 0,1,…,n
(1)
,
m
= 0,1,…,n
(1)
Доказательство.

 - число слагаемых
в сумме (число способов выбрать среди
n
мест ровно m
мест, где
будут стоять «1»).
- число слагаемых
в сумме (число способов выбрать среди
n
мест ровно m
мест, где
будут стоять «1»).
Имеем

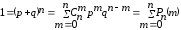
 (2)
(2)
(1) – формула Бернулли или биномиальный закон распределения.
(2)
- свойство
нормировки
вероятностей
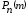 .
.
 (3)
(3)
-
Схема испытаний Бернули. Формула Пуассона
Теорема Пуассона.
Пусть m
- число успехов
в n
испытаниях Бернулли с вероятностью
успеха p.
Если
 ,
,
 так, что
так, что
 ,
то
,
то
 (4)
(4)
Доказательство.
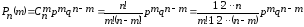 =
=
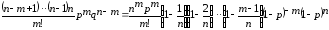 (5)
(5)
 ,
,
 ,
,

 ,
,

Тогда из (5)

-
Локальная предельная теорема Муавра – Лапласа
Локальная
предельная теорема Муавра – Лапласа.
Пусть m
- число успехов
в n
испытаниях Бернулли с вероятностью
успеха p,( ).
Если
).
Если
 ,
,
 ,
то для всех
,
то для всех
 из конечного интервала имеет место
из конечного интервала имеет место
 (6)
(6)
То есть при n>>1, m>>1
 (7)
(7)
Если
 ,
то
,
то

-
Интегральная предельная теорема
Интегральная
предельная теорема Муавра – Лапласа.
Пусть имеется
схема n
испытаний Бернулли c
вероятностью успеха p,
( ).
Пусть m-
число успехов,
q=1-p,
a<b.
Тогда
).
Пусть m-
число успехов,
q=1-p,
a<b.
Тогда
 (8)
(8)
Если
 - Ф-функция.
(9)
- Ф-функция.
(9)
то
 (10)
(10)
 (11)
(11)
Свойства
функции
 :
:
 ,
,
 ,
,

Действительно
 =
=




Наряду с функцией (9) в практике нашла применение функция
 (12)
(12)
Очевидно,

Функции
 ,
,
 табулированы.
табулированы.
