ГОУ ВПО Кемеровский Государственный Университет

Реферат по теме:

«Вариационное исчисление. Уравнение Эйлера»

Выполнил: студент группы М-092

Кемский С. О.

Кемерово 2014

Содержание

1. Вариация и ее свойства

2. Уравнение Эйлера

3. Примеры

4. Список литературы

Вариация и ее свойства

Методы решения вариационных задач, то есть задач на исследование функционалов на максимум и минимум, весьма сходны с методами исследования на максимум и минимум функций. Поэтому целесообразно напомнить кратко теорию максимума и минимума функций и параллельно ввести аналогичные понятия и доказать сходные теоремы для функционалов.

1. Переменная величина v называется функционалом, зависящим от функции y(x), что обозначается так: v = v[y(x)], если каждой функции у(х) из некоторого класса функций у(х) соответствует значение v, то есть имеет место соответствие: функции у (х) соответствует число v. Аналогично определяются и функционалы, зависящие от нескольких функций, и функционалы, зависящие от функций нескольких независимых переменных.

2. Приращением или вариацией аргумента y(x) функционала v[y(x)] называется разность между двумя функциями . При этом предполагается, что y(x) меняется произвольно в некотором классе функций.

3. Функционал v[y(x)] называется непрерывным, если малому изменению y(x) соответствует малое изменение функционала v[y(x)].

Последнее определение нуждается в уточнении и разъяснении, так как сейчас же возникает вопрос, какие изменения функции у(х), являющейся аргументом функционала, называются малыми или, что то же самое, какие кривые и считаются мало отличающимися или близкими.

Можно считать близкими функции у(х) и в том случае, если модуль их разности мал для всех значений х, для которых задаются функции у(х) и , то есть считать близкими кривые, близкие по ординатам.

Однако при таком определении близости кривых часто встречающиеся в приложениях функционалы вида

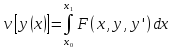
из-за наличия в подынтегральной функции аргумента у' лишь в исключительных случаях будут непрерывными. Поэтому во многих случаях более естественно считать близкими только те кривые, которые близки по ординатам и по направлениям касательных в соответствующих точках, то есть требовать, чтобы для близких кривых не только модуль разности был бы мал, но, кроме того, был бы мал и модуль разности .

Кривые и близка в смысле близости нулевого порядка, если модуль разности мал.

Кривые и близки в смысле близости первого порядка, если модули разностей и малы.

Аналогично для k-го порядка.

3*. Функционал v[y(x)] непрерывен при в смысле близости k-го порядка, если для любого положительного можно подобрать такое, что при

При этом подразумевается, что функция у (х) берется из класса функций, на котором функционал v[у(х)] определен.

4. Линейным функционалом называется функционал , удовлетворяющий следующим условиям:

где произвольная постоянная и .

5. Если приращение функционала можно представить в виде , то называется вариацией функционала и обозначается .

Итак, вариация функционала — это главная, линейная по отношению к бу, часть приращения функционала.

Уравнение Эйлера

Исследуем на экстремум функционал

­­

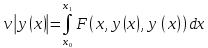
причем граничные точки допустимых кривых закреплены: и (рис. 1). Функцию будем считать трижды дифференцируемой.

Рисунок 1

Мы уже знаем, что необходимым условием экстремума является обращение в нуль вариации функционала. Покажем теперь, как применяется эта основная теорема к рассматриваемому функционалу, причем мы еще раз повторим предыдущее рассуждение применительно к функционалу). Предположим, что экстремум достигается на дважды дифференцируемой кривой у = у (х) (требуя лишь существования производных первого порядка у допустимых кривых, можно иным методом доказать, что у кривой, реализующей экстремум, существует и вторая производная).

Возьмем какую-нибудь близкую к у = у(х) допустимую кривую и включим кривые у = у(х) и в однопараметрическое семейство кривых

при получим кривую , при имеем 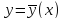(рис. 2). Как мы уже знаем, разность называется вариацией функции у(х) и обозначается .

Вариация в вариационных задачах играет роль, аналогичную роли приращения независимого переменного в задачах на исследование экстремумов функций . Вариация функции является функцией х. Эту функцию можно дифференцировать один или несколько раз, причем т. е. производная вариации равна вариации производной, и аналогично

Итак, рассмотрим семейство где , содержащее при кривую, на которой достигается экстремум, а при —некоторую близкую допустимую кривую — так называемую кривую сравнения.

Если рассматривать значения функционала

Рисунок 2

только на кривых семейства , то функционал превращается в функцию:

так как значение параметра 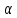определяет кривую семейства и тем самым определяет и значение функционала . Эта функция достигает своего экстремума при , так как при получаем у = y(х), и функционал, по предположению, достигает экстремума по сравнению с любой близкой допустимой кривой и, в частности, по отношению к близким кривым семейства 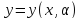. Необходимым условием экстремума функции при , как известно, является обращение в нуль ее производной при :

Так как

то

где

или, так как

и

получим

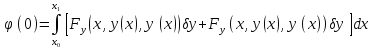
Как мы уже знаем, называется вариацией функционала и обозначается . Необходимое условие экстремума функционала заключается в обращении в нуль его вариации: 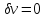. Для функционала

это условие имеет вид

Интегрируем второе слагаемое по частям и, принимая во внимание, что 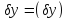, получим

Но

потому что все допустимые кривые в рассматриваемой простейшей задаче проходят через фиксированные граничные точки, и следовательно,

Итак, необходимое условие экстремума приобретает вид

причем первый множитель на кривой у = у(х), реализующей экстремум, является заданной непрерывной функцией, а второй множитель , ввиду произвола в выборе кривой сравнения является произвольной функцией, удовлетворяющей лишь некоторым весьма общим условиям, а именно: функция в граничных точках и обращается в нуль, непрерывна и дифференцируема один или несколько раз, или и малы по абсолютной величине.

Для упрощения необходимого условия экстремума воспользуемся следующей леммой:

Основная лемма вариационного исчисления. Если для каждой непрерывной функции

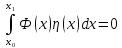
где функция Ф(х) непрерывна на отрезке , то на том же отрезке.

Применим теперь основную лемму для упрощения полученного выше необходимого условия экстремума простейшего функционала

Все условия леммы выполнены: на кривой, реализующей экстремум, множитель является непрерывной функцией, а вариация является произвольной функцией, на которую наложены лишь предусмотренные в основной лемме ограничения общего характера, следовательно, на кривой у = у (х), реализующей экстремум рассматриваемого функционала, т. е. у = у (х) является решением дифференциального уравнения второго порядка

или в развернутом виде

Это уравнение называется уравнением Эйлера (оно впервые было им опубликовано в 1744 году). Интегральные кривые уравнения Эйлера называются экстремалями. Только на экстремалях может достигаться экстремум функционала

Для нахождения кривой, реализующей экстремум функционала, интегрируем уравнение Эйлера и определяем обе произвольные постоянные, входящие в общее решение этого уравнения, из условий на границе , . Только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функционала.

Напомним, что краевая задача

не всегда имеет решение, а если решение существует, то оно может быть не единственным.

Заметим, что во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи, и если решение уравнения Эйлера, удовлетворяющее граничным условиям, единственно, то эта единственная экстремаль и будет решением рассматриваемой вариационной задачи.