1. Тестовые задания

1. Укажите факторы, связанные наиболее тесно корреляционной зависимостью, если известны значения коэффициентов корреляции: r_ху =0,35, r_yz = 0,78 и r_xz = -0,83.

1. х и z;

2. х и у;

3. r и у;

4. все факторы не связаны между собой тесной корреляционной связью.

2. Линейный парный коэффициент корреляции изменяется в пределах:

1. ;

2. -1<r<+1;

3. ;

4. ;

5. -<r<+.

3. При наличии функциональной линейной зависимости между количественными признаками X и Y коэффициент корреляции r_ху=... .

4. Обратную связь между признаками показывает коэффициент корреляции ...

1. r_ху= 0,982; B. r_ху= -0,991; C. r_ху = 0,871.

5. Для измерения тесноты корреляционной связи между двумя количественными признаками используются ... .

1. коэффициент корреляции знаков;

2. коэффициент эластичности;

3. линейный коэффициент корреляции;

4. коэффициент корреляции рангов.

6. Тесноту связи между двумя качественными альтернативными признаками можно измерить с помощью коэффициентов ... .

1. знаков Фехнера;

2. корреляции рангов Спирмена;

3. ассоциации;

4. контингенции;

5. конкордации.

7. Коэффициент детерминации может принимать значения ... .

1. от 0 до 1;

2. от-1 до 0;

3. от -1 до 1;

4. любые положительные;

5. любые меньше нуля.

8. В результате проведения регрессионного анализа получают функцию, описывающую ... показателей.

1. взаимосвязь;

2. соотношение;

3. структуру;

4. темпы роста;

5. темпы прироста.

9. Прямолинейная связь между факторами исследуется с помощью уравнения регрессии ... .

1. ;

2. ;

3. ;

4. .

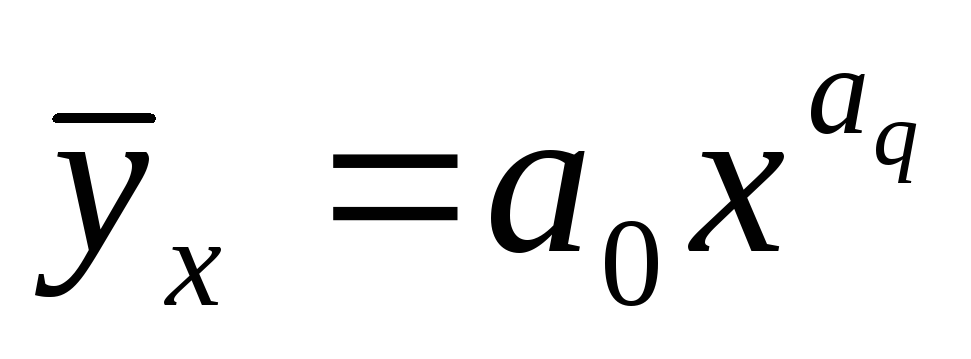10. Параметр a₁ (a₁= 0,016) линейного уравнения регрессии показывает, что:

1. с увеличением признака "х" на 1 признак "у" увеличивается на 0,694;

2. с увеличением признака "х" на 1 признак "у" увеличивается на 0,016;

3. связь между признаками "х" и "у" прямая;

4. связь между признаками "х" и "у" обратная.

Медведева т.Ю. Статистика (общая теория статистики)

Практикум

Подписано к печати:

Тираж:

Заказ №

99