Теплоемкость кристаллов. Закон Дюлонга-Пти. Теория теплоемкости Эйнштейна и Дебая

Расположение частиц в узлах отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из узла решетки возникает возвращающая сила, вследствие которой возникнут колебания частиц, которые можно представить как наложение колебаний вдоль трех координатных осей, т.е. приписать колебанию частицы три колебательные степени свободы. На каждую колебательную степень свободы приходится энергия, равная kT (1/2 kT – в виде кинетической и 1/2 kT – в виде потенциальной энергии). Следовательно, на каждую частицу в узле решетки приходится энергия, равная 3 kT, а энергия одного моля вещества будет равна внутренней энергии U

U = 3N_AkT = 3 RT

и молярная теплоемкость твердого тела (для них С_v = С_p )

C = = 3R.

Это соотношение носит название закона Дюлонга-Пти. Этот закон выполняется только при температурах близких к нормальной и не выполняется при низких температурах.

Для выяснения зависимости теплоемкости кристаллов Эйнштейн предложил теорию, в которой систему из N атомов представил в виде 3N независимых гармонических осцилляторов, колеблющихся с одинаковой частотой ν. Энергия каждого гармонического осциллятора может иметь значения

n = 0, 1, 2, 3, …

Тогда для системы 3N осцилляторов энергия будет равна

,

а теплоемкость твердого тела равна

,

где - характеристическая температура Эйнштейна из условия, что hν = Θ_Ek. Это формула теплоёмкости кристаллов по теории Эйнштейна.

При высоких температурах когда kT» hν теплоемкость 1моля будет равна

С = 3N_Ak = 3R.

т.е. отражает закономерность Дюлонга-Пти.

При низких температурах (kT«hν) эта формула качественно правильно описывает ход снижения теплоемкости твердого тела, но все же расходится с опытными данными для температур близких к абсолютному нулю

Пренебрегая единицей в знаменателе, получим выражение для теплоёмкости

.

При Т→0 экспоненциальный множитель изменяется значительно быстрее, чем Т². Поэтому при приближении к абсолютному нулю теплоёмкость будет стремиться к нулю по экспоненциальному закону. Опыт показывает, что теплоёмкость кристаллов вблизи абсолютного нуля изменяется не экспоненциально по закону Т³.

Дебай посчитал, что предположение Эйнштейна о равенстве частот всех гармонических осцилляторов является чрезмерно упрощенным. Он предположил, что гармонические осцилляторы обладают спектром (набором) частот, общее число которых ограничено и равно 3N. В соответствии с этим Дебай получил формулы для молярных (С_м) теплоёмкостей кристаллов

- при высоких температурах и

- при низких температурах.

где - характеристическая температура Дебая.

Это соотношение носит название закона кубов Дебая.

Понятие о зонной теории твердых тел

Взаимодействие электронов и ядер в свободном атоме является весьма сложным. Еще более сложно описать их взаимодействие в кристалле, где каждая частица взаимодействует с огромным числом соседних частиц. Известно, что в изолированном атоме электроны находятся в дискретных энергетических состояниях. Из соотношения неопределенностей для энергии и времени

ΔЕ·Δt

ширина энергетического уровня для электрона в свободном возбужденном атоме (Δt∼10^-8 с) составляет величину порядка 10^-7 эВ, а в основном состоянии (Δt→∞) –ΔЕ ≃0. Для электронов в кристалле ширина энергетического уровня от 1 до 10 эВ. Почему возрастает неопределенность в определении энергии электронов атома в кристалле?

В свободном атоме энергетические состояния определяются взаимодействием их с ядром своего атома. При сближении двух атомов на расстояние менее 10^-10м А электронные оболочки валентных (внешних) электронов настолько перекроются, что энергетические уровни уже не будут соответствовать энергетическим уровням электронов свободного атома. В отличие от изолированных атомов, где энергетические уровни электрона представляют резкие линии (определенные значения), при образовании кристалла происходит расщепление уровней и энергетический спектр электронных состояний представляет собой совокупность энергетических уровней, называемых зоной.

Расщепление уровней присуще всем электронам атома, но величина расщепления для разных уровней разная.

Для внутренних оболочек величина расщепления очень мала и внутренние электроны в кристалле ведут себя практически также как и в изолированных атомах.

В результате расщепления энергетических уровней область возможных значений энергии электронов кристалла разделяется на ряд зон (рис. 181) – разрешенных и запрещенных значений энергии. С уменьшением энергии ширина разрешенных зон убывает, а запрещенных – возрастает.

Энергетическая зона не является непрерывным рядом значений энергий электрона, а представляет собой ряд конкретных дискретных уровней, отстоящих друг от друга на величину порядка 10^-22 эВ. Разрешенные энергетические зоны в кристалле могут быть по разному заполнены электронами – в предельных случаях либо полностью свободны, или целиком заполнены.

Возможны переходы электронов из одной разрешенной зоны в другую. Для этого необходимо затратить энергию, численно равную ширине запрещенной зоны. Для внутризонных переходов с уровня на уровень требуется очень небольшая энергия (10^-4 – 10^-8 эВ). Существование энергетических зон позволяет объяснить разделение твердых веществ по электропроводности на металлы, полупроводники и диэлектрики (рис. 182). Электропроводность металла объясняется тем, что электроны валентной зоны (у металлов она является и зоной проводимости) под действием незначительной сообщенной им энергии могут совершать внутризонные переходы, а поскольку они слабо связаны с узлами кристаллической решетки, то под действием слабого электрического поля могут ускоряться и приобретать дополнительную скорость в направлении противоположном полю, т.е. обеспечивать электрический ток.

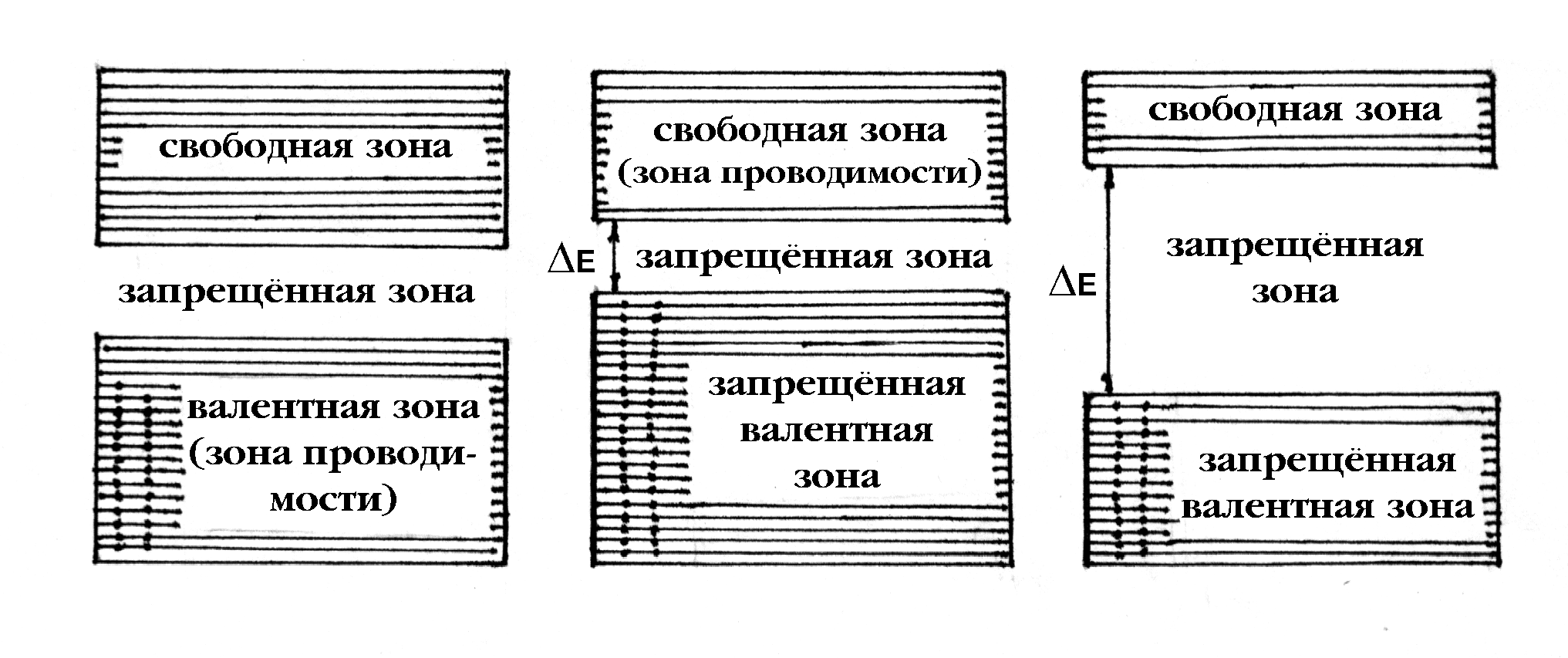
У полупроводников валентная зона полностью заполнена и для вовлечение электронов в электрический ток им необходимо сообщить энергию не меньшую ширины запрещенной зоны, т.е. перевести электроны из валентной в свободную зону. Ширина запрещённой зоны у полупроводников имеет величину порядка 1эВ.

Еще большая энергия требуется для перевода электрона из валентной в зону проводимости (свободную зону) у изоляторов, почему они и не проводят электрический ток.

У металлов две соседние разрешенные зоны могут перекрываться и тогда переход электрона из валентной зоны в свободную по энергетическим затратам эквивалентен внутризонному переходу.