5.2. Критерий устойчивости Рауса – Гурвица

В наиболее распространенном на практике случае использование этого критерия сводится к составлению из коэффициентов уравнения (5.1) матрицы следующего вида:

Порядок составления этой матрицы достаточно прост; первая строка заполняется коэффициентами характеристического уравнения с нечетными индексами, а вторая – с четными; каждая последующая пара строк есть повторение предыдущей пары, но сдвинутой на один столбец вправо. Места, где отсутствуют коэффициенты, заполняются нулями.

Анализ устойчивости системы состоит в том, что по этой матрице последовательно проводят вычисление определителей квадратных матриц:

;;и т.д.

Вычисления следует прекратить, если очередной определитель окажется отрицательным, поскольку это свидетельствует о неустойчивости системы. Если же все определителей окажутся положительными, то это свидетельствует об устойчивости системы, т. е. условие устойчивости записывается следующим образом:

;; ...;;.

В частности, эти условия имеют вид:

1. Для систем первого () и второго () порядков условия устойчивости сводятся к положительности коэффициентов характеристического уравнения.

2. Для системы третьего () порядка характеристическое уравнение принимает вид

,

а условие устойчивости выражается следующими неравенствами:

; ;;;.

3. Для системы четвертого () порядка характеристическое уравнение представимо в виде

,

а условие устойчивости выражается следующей системой неравенств:

Из рассмотренного критерия следует, что необходимым, но недостаточным условием устойчивости является положительность всех коэффициентов уравнения (5.1).

Критерий Рауса–Гурвица позволяет не только анализировать устойчивость систем с заданными численными значениями коэффициентов характеристического уравнения, но и решать обратную задачу определения допустимых по условию устойчивости значений этих коэффициентов (или связанных с ними параметров системы). Для этого, очевидно, неравенства (5.5), выраженные через неизвестные значения исследуемых коэффициентов, следует заменить равенствами; полученная таким образом система уравнений в пространстве исследуемых коэффициентов определяет границы областей, где выполняются соответствующие неравенства. Пересечение найденных областей (общая область) и определяет область устойчивости системы.

5.3. Критерий устойчивости Михайлова

Будем рассматривать характеристический полином замкнутой системы как функцию комплексной переменной, значения которой изменяются при изменении . В частности, приэтот полином принимает следующий вид:

.

При фиксированном значении он изображается в комплексной плоскости вектором

; ,

получившим название характеристического;при измененииконец характеристического вектора очерчивает кривую –годограф характеристического вектора.

Критерий Михайлова формулируется следующим образом: система с характеристическим уравнением -го порядка устойчива, если при измененииот 0 догодограф характеристического вектора, начинаясь на вещественной положительной полуоси, проходит против часовой стрелки последовательноквадрантов комплексной плоскости, или, иначе говоря, характеристический вектор поворачивается против часовой стрелки на угол.

С целью иллюстрации применения критерия Михайлова для оценки устойчивости систем рассмотрим пример.

Пример 5.1.Проанализируем на устойчивость систему, имеющую характеристическое уравнение четвертого порядка

.

При характеристический полиномпринимает вид

.

Следовательно, его вещественная и мнимая части задаются выражениями

;.

Полагая, что

;;;;,

построим годограф Михайлова, описываемый характеристическим вектором

,

при изменении значения частоты отдо. Данный годограф представлен на рис. 5.1.

Рис. 5.1.

Согласно рис. 5.1 годограф Михайлова, начавшись на положительной вещественной полуоси, проходит против часовой стрелки последовательно четыре квадранта комплексной плоскости. Следовательно, исследуемая система является устойчивой.

Рассмотрим также случай, когда коэффициенты характеристического уравнения заданы равенствами

;;;;.

Построим годограф Михайлова, описываемый характеристическим вектором

.

Вид этого годографа показан на рис. 5.2.

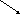
Рис. 5.2.

Поскольку годограф Михайлова последовательно проходит все положенные квадранты, кроме одного, пропущенного из–за прохождения через начало координат, то система находится на границе устойчивости, генерируя незатухающие синусоидальные колебания с частотой , при которой годограф проходит через начало координат.

Пусть

;;;;,

тогда

.

В этом случае система неустойчива, т.к. годограф не может выйти за пределы вещественной оси и пройти положенное число квадрантов комплексной плоскости.

Предположим, что

;;;;,

тогда

.

Годограф Михайлова для рассматриваемой системы изображен на рис. 5.3.

Рис. 5.3.

Поскольку годограф Михайлова проходит лишь два квадранта комплексной плоскости и не в надлежащей последовательности, то система неустойчива.

Рассмотренный пример показывает, что в тех случаях, когда известен характеристический полином , критерий Михайлова удобно использовать при анализе систем на устойчивость.