II Дана структурная схема замкнутой сар.

где

T	-	0,5;
T1	-	1;
ξ	-	0,1;
К	-	1.

Необходимо:

1. Записать передаточную функцию разомкнутой системы.

2. Записать передаточную функцию замкнутой системы.

3. Определить, является ли данная система устойчивой (по критерию Михайлова).

1 Сложные элементы автоматических систем и сами автоматические системы состоят из некоторого числа соединенных между собой динамических звеньев. Наиболее простыми и часто встречающимися соединениями являются последовательное (рисунок 1,а), параллельное (1,б) соединение, называемое встречно-параллельным или - охват звена обратной связью (рисунок 1,в)

a)

б) в)

Рисунок 1 - Типовые соединения динамических звеньев: а) последо­ватель­ное; б) параллельное; в) звено , охваченное обратной связью посредством звена

При последовательном соединении выходная величина каждого из звеньев, кроме последнего, служит входной величиной последующего звена. Эквивалентная передаточная функция последовательного соединения в общем случае определяется по формуле

(1)

При параллельном соединении все звенья имеют одну и ту же входную величину, а их выходные величины суммируются. Передаточная функция параллельного соединения n звеньев равна

(2)

Соединение звеньев, представленное на рисунок 1,в приводит к образованию замкнутой системы и состоит из двух звеньев. Звено с передаточной функцией является прямой цепью передачи сигналов, а звено с передаточной функциейосуществляет обратную связь. Обратная связь - это воздействие выходной величины какого-то звена на его вход. Если это воздействие совпадает по знаку с входной величиной, то обратная связь - положительная. В противном случае обратная связь - отрицательная.

Передаточная функция замкнутой автоматической системы

(3)

где знак "+" в знаменателе соответствует отрицательной обратной связи и знак "-" - положительной.

Исходя из вышеизложенного, определим передаточную функцию разомкнутой системы.

.

2. Передаточную функцию замкнутой системы найдем по формуле 3

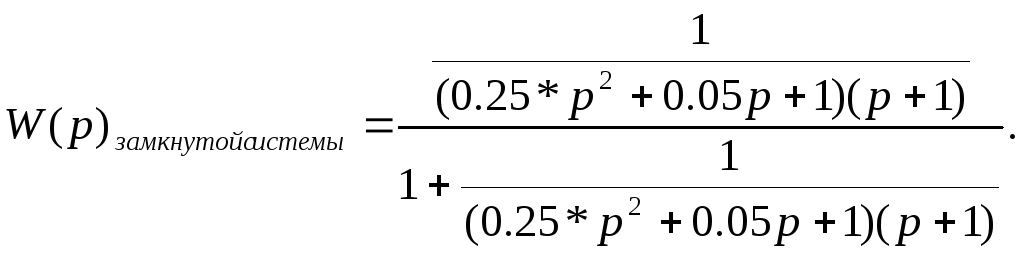
Упростив выражение, получим:

3. Теорема (критерий Михайлова). Для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова, начинаясь при ω=0 на действительной оси, с увеличением ω от 0 до ∞ обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n – порядок характеристического уравнения.

Годограф Михайлова – это геометрическое место точек конца вектора на комплексной плоскости (годограф Михайлова). (- характеристический полином системы).

Для построения годографа Михайлова используем программный пакет Маткад.

Как видно из графика, годограф Михайлова охватывает I, IV, III квадрант. Таким образом, по критерию Михайлова, данная система является неустойчивой.

Дополнительно исследуем систему на устойчивость по критерию Найквиста. При этом известно, что данная система в разомкнутом состоянии устойчива.

Теорема (критерий Найквиста). Для устойчивости САУ необходимо и достаточно, чтобы годограф разомкнутой системы при измененииω от 0 до ∞ охватывал l/2 раз в положительном направлении точку (-1, i0), где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Из этой теоремы непосредственно вытекает:

Следствие. Если разомкнутая система устойчива (l=0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф при измененииω от 0 до ∞ не охватывал точку (-1, i0).

Заметим, что для применении частотного критерия устойчивости Найквиста необходимо знать, устойчива или неустойчива система в разомкнутом состоянии. При этом, если система в разомкнутом состоянии неустойчива, то следует определить количество корней её характеристического уравнения, имеющих положительные вещественные части. Только в этом случае можно применить частотный критерий устойчивости Найквиста к исследованию устойчивости замкнутой системы.

Тест программы в Маткад будет выглядеть следующим образом:

Поскольку система в разомкнутом состоянии устойчива, годограф системы не должен охватывать точку с координатами (-1, i0). В данном случае условие нарушается, следовательно, система не устойчива.

До этого мы рассматривали частотные критерии. Исследуем устойчивость системы по критерию Гурвица.

Пусть дано характеристическое уравнение системы

Составим определитель Гурвица из коэффициентов данного уравнения:

.

Алгоритм составления определителя ясен из его структуры. По главной диагонали последовательно записываются n коэффициентов характеристического уравнения, начиная с . Столбцы определителя, начиная от элементов главной диагонали, заполняются вверх по возрастающим индексам, вниз – по убывающим. Коэффициенты с индексом меньше нуля или большеn заменяются нулями.

Теорема. Для устойчивости линейной системы автоматическго управления (САУ), необходимо и достаточно, чтобы были положительны все главные диагональные миноры определителя Гурвица:

Запишем характеристический полином замкнутой системы.

Составим матрицу Гурвица:

Поскольку определителииотрицательны, система является неустойчивой.

Таким образом, мы исследовали систему на устойчивость.