Вариант 40

1. Дано дифференциальное уравнение звена

.

Необходимо:

1. Определить передаточную функцию звена.

2. Определить переходную функцию звена .

3. Определить весовую функцию звена .

4. Определить КЧХ звена.

5. Определить ВЧХ и МЧХ звена.

2. Дана структурная схема замкнутой САР.

где

T	-	0,2;
T1	-	1;
ξ	-	0,01;
К	-	1.

Необходимо:

1. Записать передаточную функцию разомкнутой системы.

2. Записать передаточную функцию замкнутой системы.

3. Определить, является ли данная система устойчивой (по критерию Михайлова).

Теоретические вопросы.

1. Необходимое условие устойчивости.

2. Передаточная функция импульсной системы.

3.2 Пример выполнения практических заданий контрольной работы

I Дано дифференциальное уравнение звена

Необходимо:

1. Определить передаточную функцию звена.

2. Определить переходную функцию звена .

3. Определить весовую функцию звена .

4. Определить КЧХ звена.

5. Определить ВЧХ и МЧХ звена.

1. Определим передаточную функцию, если известно дифференциальное уравнение.

Для этого вынесем за скобки y(t).

Передаточная функция системы – отношение изображения по Лапласу её выходного сигнала к изображению по Лапласу её входного сигнала при нулевых начальных условиях.

Тогда

2. Определим переходную функцию звена:

Переходная характеристика ­– это реакция системы на единичное ступенчатое воздействие (скачок).

Для определения переходной функции в Маткаде воспользуемся панелью инструментов Symbolic:

Для редактирования графика необходимо щелкнуть по нему правой кнопкой мыши

В открывшемся окне можно выбрать необходимые настройки.

3. Определим весовую функцию звена (весовая или импульсная переходная характеристика – это реакция системы на единичный импульс.):

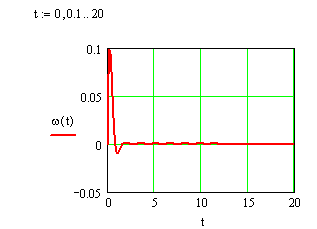
Частотной характеристикой линейной системы или, что эквивалентно, комплексной частотной функцией (КЧХ) линейной системы называется функция W(i), получаемая из передаточной функции системы при подстановке p=i. {КЧХ объекта широко используются при анализе систем управления на устойчивость, а также при расчетах параметров настройки регуляторов.4

Построим амплитудно – фазочастотную характеристику (годограф) звена

Далее применим функции MathCad:

Выберем последовательно категорию комплексные числа, далее – функцию Re (вещественная часть) и Im (мнимая часть):

Таким образом, получим:

Внимание! Для набора мнимой единицы необходимо использовать панель инструментов Calculator

Далее остается построить годограф звена.

Аналогично строится ВЧХ и МЧХ:

Вещественная частотная характеристика:

Мнимая частотная характеристика:

Амплитудная частотная характеристика есть модуль комплексного числа. Исходя из этого, найдем АЧХ звена.

Фазо-частотная характеристика есть аргумент комплексного числа. Исходя из этого, найдем ФЧХ звена.

Таким образом, с применением программы MathCad нами получены частотные характеристики звена, а также весовая и переходная функция.