Центральная предельная теорема

Рассмотрим распределение вероятностей суммы очков на игральных костях. На рисунках ниже приведены многоугольники распределения для случая одной, двух и трех костей.

Видно, что с увеличением числа костей многоугольник распределения все более становится похожим на график плотности нормального закона. Эта близость к нормальному закону становится еще более разительной при еще большем числе костей.

Оказывается, такая близость суммы большого числа случайных величин к нормальному закону распределения является закономерной и носит в теории вероятности название центральной предельной теоремы.

В грубой формулировке эта теорема выглядит так:

Сумма большого числа независимых случайных величин при довольно широких предположениях подчинена нормальному закону распределения.

Перейдем теперь к более точным формулировкам.

ОПРЕДЕЛЕНИЕ 1. Говорят, что последовательность независимых случайных величин Х₁,Х₂,...Х_n удовлетворяет условиям Ляпунова, если

ЗАМЕЧАНИЕ. Рассмотрим один практически важный случай, когда независимые случайные величины имеют один и тот же закон распределения. Тогда

,

т.е. условие Ляпунова в этом случае выполнено.

Смысл сделанного замечания заключается в том, что для выполнения условия Ляпунова все случайные величины должны иметь примерно одинаковое распределение, т.е. ни одна из них не должна резко выделяться среди остальных.

Дадим теперь точную формулировку центральной предельной теоремы, которую примем без доказательства.

ТЕОРЕМА. Если последовательность Х₁,Х₂,...Х_n независимых случайных величин удовлетворяет условию Ляпунова, то

Эта теорема показывает, что на практике и в теории нормальное распределение играет особую, центральную роль, коль скоро речь идет о большом числе случайных величин, а на практике такая ситуация встречается достаточно часто.

ПРИМЕР 2. Завод выпускает валы турбогенераторов с номинальным диаметром D. Из-за множества складывающихся случайных влияний (температура, вибрация, неидеальная технология, неоднородность материала, ошибки измерений и т.д.) диаметр изготавливаемых валов D является случайной величиной. Если все факторы влияют примерно одинаково (условия Ляпунова), то - это нормально распределенная случайная величина.

Рассмотрим еще одно приложение центральной предельной теоремы, с которым мы уже сталкивались.

Рассмотрим схему Бернулли с числом «успехов» Х==Х₁ +Х₂ +...+Х_n Случайные величины X_i независимы и имеют один и тот же закон распределения (см.п.2.1). Вычислим вероятность того, что число успехов будет в пределах от k₁ до k₂ , когда число испытаний неограниченно возрастает. Применяя центральную предельную теорему, получаем

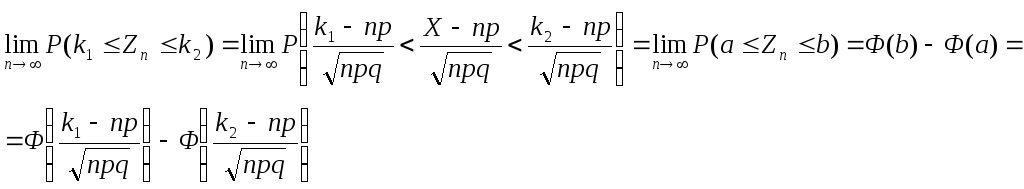
где мы использовали ранее полученные формулы

М[Х]=nр, D[Х]=nрq.

Когда n большое, но конечное, имеем приближенную формулу

Эта формула не что иное как приближенная интегральная формула Лапласа, которую мы без доказательства использовали для подсчета аналогичной вероятности.

 

Точечные и интервальные оценки случайных величин. Доверительный интервал. Доверительная вероятность. Аппроксимация экспериментальных зависимостей по методу наименьших квадратов.

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки, полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр. Рассматривая значения количественного признака как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения - это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

  Несмещенной называют статистическую оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.

M(Q^*) = Q.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

  Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую  возможную дисперсию.

При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

  Состоятельной называют статистическую оценку, которая при п стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п  стремится к нулю, то такая оценка оказывается и состоятельной.

Рассмотрим точечные оценки параметров распределения, т.е. оценки, которые определяются одним числом Q^* =f( x₁, x₂,…,x_n), где x₁, x₂,…,x_n- выборка.

Пусть изучается генеральная совокупность относительно количественного признака Х.

  Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения признака различны, то

Если значения признака имеют частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

  Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

если же все значения имеют частоты n₁, n₂,…,n_k, то

Выборочная средняя является несмещенной и состоятельной  оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Если все значения признака генеральной совокупности объема N различны, то

Если же значения признака имеют соответственно частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

  Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

  Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

 если же все значения имеют частоты n₁, n₂,…,n_k, то

Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

  Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

 

  Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .

Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного пара­метра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если >0 и |Q- Q*| < , то чем меньше  , тем оценка точнее.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <; можно лишь говорить о вероятности , с которой это неравенство осуществляется.

  Надежностью (доверительной вероятностью) оценки называют вероятность  , с которой осуществляется неравенство |Q—Q* | < .

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| <d равна g: P(|Q- Q*| <d)= g. Заменив неравенство равносильным ему двойным неравенством получим: Р [Q* —< Q < Q* +] =    Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.

  Интервал (Q* -  Q* +) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью .

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение  этого распределения -. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью . Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки  к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением . Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами

.Потребуем, чтобы выполнялось равенство

Заменив Х и , получим

 

получим

Задача решена.  Число t находят по таблице функции Лапласа Ф(х).

Пример1. СВХ распределена нормально и s =3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, если n = 36 и задана надежность  =0,95.

Из соотношения 2Ф(t)= 0,95 , откуда Ф(t) = 0,475 по таблице  найдем t : t =1,96. Точность оценки

Доверительный интервал

  .

Пример2. Найти минимальный объем выборки, который обеспечивает заданную точность d =0,3 и надежность g = 0,975, если СВХ распределена нормально и s =1,2.

Из равенства

выразим n:

,

подставим значения и получим минимльный объем выборки  n ~ 81.

Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.

В качестве неизвестного параметра sиспользуют исправленную дисперсию s² . Заменяя  на s, t на величину t_. Значение  этой величины зависит от надежности  и объема выборки n  и определяется  по " Таблице значений t_."  Итак :

и доверительный интервал имеет вид

Пример1. Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если объем выборки n =16, среднее выборочное и исправленная дисперсия соответственно равны 20,2 и 0,8.

По таблице приложения найдем t_по заданной надежности  =0,95 и n= 16: t_ =2,13. Подставим в формулу s =0,8 и t_ =2,13 , вычислим границы доверительного интевала:

,

откуда получим доверительный интервал (19,774; 20,626)

Смысл полученного результата: если взять 100 различных выборок, то в 95 из них математическое ожидание будет находится в пределах данного интервала, а в 5 из них- нет.

Пример2. Измеряют диаметры 25 корпусов электродвигателей. Получены выборочные характеристики

 

Необходимо найти вероятность (надежность) того, что

- является доверительным интервалом оценки математического ожидания при нормальном распределении.

Из условия задачи найдем точность d, составив и решив систему:

 Откуда d =10.   Из равенства 

выразим  

,

откуда t_ =3,125. По таблице для найденного t_  и n= 25 находим  =0,99.

Доверительный интервал для оценки дисперсии и среднего квадратического отклонения.

Требуется оценить неизвестную генеральную дисперсию и генеральное среднее квадратическое отклонение по исправленной дисперсии, т.е. найти доверительные интервалы, покрывающие параметры D и  с заданной надежностью .

Потребуем выполнения соотношения

.

Раскроем модуль и получим двойное неравенство:

.

Преобразуем:

.

Обозначим d/s = q (величина q находится по  "Таблице значений q"и зависит от надежности и объема выборки), тогда доверительный интервал для оценки генерального среднего квадратического отклонения имеет вид:

.

Замечание : Так как s >0, то если q >1 , левая граница интервала равна 0:                  

 0< s < s ( 1 + q ).

Пример1.  По выборке объема n = 25 найдено "исправленное" среднее квадратическое отклонение s = 0,8.  Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,95.

По таблице приложения по данным : g = 0,95; n =25 , находим q = 0,32.

Искомый доверительный интервал 0,8(1- 0,32)< s < 0,8(1+ 0,32) или  0,544<s <0,056.

Пример2. По выборке объема n = 10 найдено s = 0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,999.

q( n=10, g =0,999) = 1,8>0.

Искомый доверительный интервал  0< s <0,16(1+1,8)  или  0< s <0,448.

Так как дисперсия есть квадрат среднего квадратического отклонения, то доверительный интервал, покрывающий генеральную дисперсию с заданной надежностью g, имеет вид:

Интервальная оценка вероятности биноминального распределения по относительной частоте.

Найдем доверительный интервал для оценки вероятности по относительной частоте, используя формулу:

 

Если n достаточно велико и р не очень близка к нулю и единице, то можно считать, что относительная частота распределена приближенно по нормальному закону, причем М(W)= р. Заменив Х на относительную частоту , математическое ожидание - на вероятность, получим равенство:

Приступим к построению доверительного интервала (р₁, р₂), который с надежностью   покрывает оцениваемый параметр р Потребуем, чтобы с надежностью g выполнялось соотношение указанное выше равенство:

Заменив

,

получим:

Таким образом, с надежностью g выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1- р вместо q):

Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р:

Дискриминант трехчлена положительный, поэтому корни действительные и различные:

меньший корень

больший корень:

 

 Замечание1: При больших значениях n , пренебрегая слагаемыми

,и

учитывая

получим приближенные формулы для границ доверительного интервала :

  

Пример1. Производят независимые испытания с одинаковой и неизвестной вероятностью появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.

По условию n =80, m=16,  =0,95. Относительная частота

  .

Из соотношения Ф(t)=0,95/2 = 0,475 по таблице находим t = 1,96. Т.к. n<100,  то используем точные формулы, получим : р₁= 0,128, р₂= 0,299.

 Замечание 2: Если n мало, то используем для определения концов доверительного интервала вероятности события при биноминальном распределении "Таблицу доверительных границ р₁ и р₂". Значения р₁ и р₂ находят в зависимости от n и m.

Пример. В пяти независимых испытаниях событие А произошло 3 раза. Найти с надежностью 0,95 интервальную оценку для вероятности события А в единичном испытании.

По условию задачи n=5, m=3. Имеет место схема повторных испытаний. Используя таблицу, находим доверительный интервал : 0,147<p<0,947.

Контрольные вопросы

1.      Определение статистической оценки неизвестного параметра.

2.      Какая оценка называется точечной?

3.      Каким требованиям должны удовлетворять статистические оценки?

4.      Сформулировать определения генеральной средней и генеральной дисперсии.

5.      Записать выражения для вычисления выборочной средней, выборочной дисперсии и исправленной дисперсии. Какая из этих оценок не является несмещенной?

6.      Методики вычисления границ доверительного интервала  для оценки математического ожидания нормально распределенной СВ при известном и неизвестном .

7.      Методика вычисления границ доверительного интервала для оценки среднего квадратического отклонения нормально распределенной СВ.

8.      Доверительный интервал вероятности биноминального распределения по относительной частоте при больших n , при n<100.

Критерии поверки статистических гипотез. Критерии Пирсона и Романовского.

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.

Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н₀. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н₁. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н₀ о равенстве l=10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н₀ о неравенстве l>10 состоит из бесконечного множества простых гипотез Н₀ о равенстве l=bi, где bi – любое число, большее 10. Гипотеза Н₀ о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, то гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Принятие или отклонение гипотезы Н₀ по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н₀ и принимается конкурирующая гипотеза Н₁. Ошибка второго рода возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н₀, в то время как справедлива конкурирующая гипотеза Н₁. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н₀. Вероятность отвергнуть ложную гипотезу Н₀ называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл.

Таблица

Гипотеза Н0	Решение	Вероятность	Примечание
Верна	Принимается	1 - a	Доверительная вероятность
	Отвергается	a	Вероятность ошибки первого рода
Неверна	Принимается	b	Вероятность ошибки второго рода
	Отвергается	1 - b	Мощность критерия

Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q), рис. 1.

 

Рис. 1. Области принятия и отклонения гипотезы

Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н₀ о равенстве q=Т, то насколько велико должно быть различие между q и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между q и Т на основе выборочного распределения параметра q.

Целесообразно полагать одинаковыми значения вероятности выхода параметра q за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность выхода параметра q за пределы интервала с границами q1–a/2 и qa/2, составляет величину a. Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства q=Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н₀. Отсюда следует, что вероятность допустить ошибку первого рода равна a (равна уровню значимости критерия).

Если предположить, например, что истинное значение параметра в действительности равно Т+d , то согласно гипотезе Н₀о равенстве q=Т – вероятность того, что оценка параметра q попадет в область принятия гипотезы, составит b, рис. 2.

 

Рис. 2. Области принятия и отклонения гипотезы

 При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a. Однако при этом увеличивается вероятность ошибки второго рода b (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т–d.

Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность a была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения a относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами q1–a/2 и qa/2 для типовых значений a и различных способов построения критерия.

При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.

В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.

Распределение хи-квадрат

Распределению хи-квадрат (c2-распределению) с k степенями свободы соответствует распределение суммы

квадратов n стандартизованных случайных величин ui, каждая из которых распределена по нормальному закону, причем k из них независимы, n>=k. Функция плотности распределения хи-квадрат с k степенями свободы

, x >= 0,

где х=c2, Г(k/2) – гамма-функция.

Число степеней свободы k определяет количество независимых слагаемых в выражении для c2. Функция плотности при k, равном одному или двум, – монотонная, а при k>2 – унимодальная, несимметричная, рис. 3

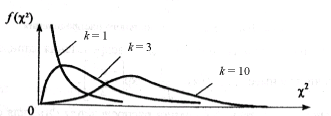
Рис. 3. Плотность распределения хи-квадрат

 Математическое ожидание и дисперсия величины c2 равны соответственно k и 2k . Распределение хи-квадрат является частным случаем более общего гамма-распределения, а величина, равная корню квадратному из хи-квадрат с двумя степенями свободы, подчиняется распределению Рэлея.

С увеличением числа степеней свободы (k>30) распределение хи-квадрат приближается к нормальному распределению с математическим ожиданием k и дисперсией 2k. В таких случаях критическое значение

c2(k; a) » u1–a(k, 2k),

где u1–a(k, 2k) – квантиль нормального распределения. Погрешность аппроксимации не превышает нескольких процентов.

 Распределение Стьюдента

Распределение Стьюдента (t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student) характеризует распределение случайной величины

где u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента

(3.5)

Величина k характеризует количество степеней свободы. Плотность распределения – унимодальная и симметричная функция, похожая на нормальное распределение, рис. 4.

Рис. 4. Плотность распределения Стьюдента

 Область изменения аргумента t от минус до плюс бесконечности. Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2. По сравнению с нормальным распределение Стьюдента более пологое, оно имеет меньшую дисперсию. Это отличие заметно при небольших значениях k, что следует учитывать при проверке статистических гипотез (критические значения аргумента распределения Стьюдента превышают аналогичные показатели нормального распределения). Таблицы распределения содержат значения для односторонней (пределы интегрирования от r(k; a ) до бесконечности)

или двусторонней (пределы интегрирования от – r(k; a) до r(k; a))

критической области. Распределение Стьюдента применяется для описания ошибок выборки при k<30. При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность Р{t>t(k; a)} = u1–a(0, k /(k–2)), где u1–a(0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.

Критерий хи-квадрат К. Пирсона. Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением Fп(x), которая приближенно подчиняется закону распределения c2. Гипотеза Н₀ о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.

Итак, пусть выборка представлена статистическим рядом с количеством разрядов y. Наблюдаемая частота попаданий в i-й разряд ni. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет Fi. Разность между наблюдаемой и ожидаемой частотой составит величину (ni–Fi). Для нахождения общей степени расхождения между F(x) и Fп(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда

.

(3.7)

Величина c2 при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k. Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y–1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y–f–1.

Очевидно, что чем меньше расхождение между теоретическими и эмпирическими частотами, тем меньше величина критерия. Область принятия гипотезы Н0 определяется условием c2<c2(k; a), где c2(k; a) – критическая точка распределения хи-квадрат с уровнем значимости a. Вероятность ошибки первого рода равна a, вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).

Пример 1. Проверить с помощью критерия хи-квадрат гипотезу о нормальности распределения случайной величины, представленной статистическим рядом в табл. 2.4 при уровне значимости a=0,05.

Решение . В примере 2.3 были вычислены значения оценок моментов:

m1=27,51, m2=0,91, s=0,96.

На основе табл. 2.4 построим табл. 1, иллюстрирующую расчеты.

Таблица 1

Номер интервала, i	1	2	3	4	5	6
ni	5	9	10	9	5	6
xi	26,37	26,95	27,53	28,12	28,70	бесконечность
F(xi)	0,117	0,280	0,5 08	0,737	0,892	1
D Fi	0,117	0,166	0,228	0,228	0,155	0,108
Fi	5,148	7,304	10,032	10,032	6,820	4,752
(ni - Fi)2/Fi	0,004	0,394	0,0001	0,1062	0,486	0,328

В этой таблице:

ni – частота попаданий элементов выборки в i-й интервал;

xi – верхняя граница i-го интервала;

F(xi) – значение функции нормального распределения;

DFi – теоретическое значение вероятности попадания случайной величины в i-й интервал

Fi=DFi*n – теоретическая частота попадания случайной величины в i-й интервал;

(ni–Fi)2/Fi – взвешенный квадрат отклонения.

Для нормального закона возможные значения случайной величины лежат в диапазоне от минус до плюс бесконечности, поэтому при расчетах оценок вероятностей крайний левый и крайний правый интервалы расширяются до минус и плюс бесконечности соответственно. Вычислить значения функции нормального распределения можно, воспользовавшись стандартными функциями табличного процессора или полиномом наилучшего приближения.

Сумма взвешенных квадратов отклонения c2=1,32. Число степеней свободы k = 6–1–2=3, так как уклонения связаны линейным соотношением

,кроме того, на уклонения наложены еще две связи, ибо по выборке были определены два параметра распределения. Критическое значение c2(3; 0,05)=7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c2<c2(3; 0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.

Понятие стационарного случайного процесса . характеристики случайной функции.

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин ,где T произвольное множество, называется случайной функцией.

Если , то параметр может интерпретироваться как время. Тогда случайная функция {X_t} называется случайным процессом. Если множество T дискретно, например , то такой случайный процесс называется случа́йной после́довательностью.

Если , где , то параметр может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случа́йным по́лем.

Данная классификация нестрогая. В частности, термин "случайный процесс" часто используется как безусловный синоним термина "случайная функция".

Случайный процесс называется стационарным, если все многомерные законы распределения зависят только от взаимного расположения моментов времени , но не от самих значений этих величин. В противном случае, он называется нестационарным.

Случайная функция называется стационарной в широком смысле, если её математическое ожидание и дисперсия постоянны, а АКФ зависит только от разности моментов времени, для которых взяты ординаты случайной функции. Понятие ввёл А. Я. Хинчин.

Если ординаты случайной функции подчиняются нормальному закону распределения, то и сама функция называется нормальной.

Случайные функции, закон распределения ординат которых в будущий момент времени полностью определяется значением ординаты процесса в настоящий момент времени и не зависит от значений ординат процесса в предыдующие моменты времени, называются марковскими.

Случайный процесс называется процессом с независимыми приращениями, если

—независимые случайные величины.

Если при определении моментных функций стационарного случайного процесса операцию усреднения по статистическому ансамблю можно заменить усреднением по времени, то такой стационарный случайный процесс называется эргодическим.

Пусть дан случайный процесс . Тогда для каждого фиксированного X_t — случайная величина. Если фиксирован элементарный исход , то  — детерминистическая функция параметра t. Такая функция называется траекто́рией или реализа́цией случайной функции {X_t}.

, где называется стандартной гауссовской (нормальной) случайной последовательностью.

Пусть , и Y — случайная величина. Тогда

является случайным процессом.

Случайные динамические процессы. Пусть случайная функция  характеризуется функцией распределения вероятностей . Функция   определяет вероятность принятия различных значений  в фиксированные моменты времени.

Вероятность для  принять в момент времени  значение в некотором интервале  записывается в виде:

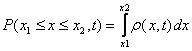.С вероятностью равной единице,  находится на интервале . Т.е. функция  должна удовлетворять условию нормировки:

   Если рассмотреть  дискретных реализаций процесса , то

, где  – число реализаций, когда значение  в момент  находится в интервале .

   Статистическое описание процесса возможно при условии, что отношение  устойчиво , т.е.

при    

   При малом  из (5.1.1) следует

• .  

• Среднее (по реализациям случайного процесса) значение  вычисляется по традиционной формуле в каждый момент времени:

.    Если  не зависит от , т.е. , то процесс называется стационарным. В дальнейшем мы ограничимся рассмотрением таких процессов.

Для вычисления среднего значения случайной функции по каждой реализации (среднее по времени) необходимо выбрать только временной интервал усреднения :

В том случае, если анализируется распределение функции , то её среднее значение вычисляется в виде

Аналогично записываются выражения для различных средних:

моменты случайного процесса

;центральные моменты:

.  Пусть необходимо найти распределение функции . Если функция однозначна, то можно построить обратную функцию . Зная распределение   найдем распределение .

   Если в интервале  

,

то перейдя к переменной , мы получим

. 

  .

   Если зависимость  многозначна и имеет несколько ветвей , то

 Корреляционные и спектральные характеристики случайного процесса. Случайный процесс называется эргодическим (эргодичным), если для него усредненное значение по времени равно усредненному значению по реализации, т.е.  при . Рассмотрим далее временные характеристики таких процессов.

   Пусть имеется две случайных функции . Взаимная корреляционная функция этих случайных процессов рассчитывается в виде

   Нормируя корреляционную функция  получим коэффициент корреляции

,

- дисперсии случайных процессов , .

   Если  и – значения одного и того же случайного процесса , то можно рассчитать коэффициент автокорреляции

.

   Если процесс стационарен, то , т.е. функция автокорреляции зависит только от временного сдвига  и не зависит от времени . Иногда это утверждение считается определением стационарного процесса.

   Кроме того, для стационарного случайного процесса функция автокорреляции симметрична, т.е. .

   Из сказанного выше следует:

.

   Характерный интервал , на котором функция автокорреляции  уменьшается в  раз, называется временем корреляции. Время корреляции определяет, насколько в случайном процессе каждое следующее во времени его значение связано с предыдущим.

 Спектральное представление случайного процесса. Запишем флуктуационную составляющую случайного процесса

,  и представим ее в виде интеграла Фурье:

. Спектральная амплитуда  является случайной функцией частоты .

   Для вещественной функции  спектральная амплитуда комплексна и  , где «*» означает комплексное сопряжение.

   Спектральной плотностью случайного процесса по определению называется величина , такая, что

.    Для стационарных случайных процессов характерно следующее важнейшее свойство: спектральная плотность процесса является Фурье-преобразованием от автокорреляционной функции (теорема Винера-Хинчина):

Статистические характеристики стационарного случайного процесса проиллюстрированы на рис.1. Здесь показана реализация процесса (рис.1,а) и эта же реализация, подвергнутая сглаживанию методом скользящего среднего (см. главу три настоящего пособия) (рис. 1,б). Зависимости 1,2,3 соответствуют реализации, ее статистическому распределению, и автокорреляционной функции. Процесс имеет распределение, близкое к нормальному (гистограмма на рис.1,а, зависимость 2) и, практически -коррелирован, то есть имеет время корреляции  и широкий спектр (автокорреляционная функция на рис.1,а, зависимость 3). После сглаживания статистическое распределение практически не меняется, но время корреляции увеличивается, т.е. происходит высокочастотная фильтрация.

Рис.1

Во многих практических случаях для характеристики случайных процессов достаточно знать лишь его усредненные, так называемые, числовые характеристики (моментные функции). Наиболее часто используются математическое ожидание (первый начальный момент), дисперсия (второй центральный момент), ковариационная функция и корреляционная функция.

Простейшей характеристикой случайного процесса является его математическое ожидание, которое представляет собой неслучайную функцию времени, около которой различным образом располагаются отдельные реализации случайного процесса.

Математическое ожидание случайного процесса - сигналов электросвязи представляет собой постоянную составляющую.

Дисперсией случайного процесса называется неслучайная функция времени, значения которой для каждого момента времени равны математическому ожиданию квадрата отклонения случайного процесса от его математического ожидания .

Дисперсия определяет степень разброса значений случайного процесса около математического ожидания.

Применительно к сигналам электросвязи дисперсия является мощностью переменной составляющей на нагрузке 1 Ом и измеряется в Ваттах.

В качестве характеристики, учитывающей статистическую связь между значениями случайного процесса в различные моменты времени, используется ковариационная функция случайного процесса, определяемая как математическое ожидание от произведения значений случайного процесса в два различных момента времени (в двух сечениях).

На практике чаще используют корреляционную функцию, которая определяется как математическое ожидание произведения центрированного случайного процесса в два различных момента времени. Центрированный процесс представляет собой только переменную составляющую.

Таким образом, числовые характеристики получаются путем усреднения соответствующей случайной величины по множеству (ансамблю) ее возможных значений. Операция усреднения по множеству обозначается прямой горизонтальной чертой сверху.

Важнейшим классом случайных процессов, встречающихся на практике, является класс стационарных случайных процессов. Случайный процесс называется стационарным в узком смысле, если его многомерная функция распределения (и, следовательно, числовые характеристики) не зависит от начала отсчета времени, т.е. от сдвига всех сечений вправо или влево на один и тот же интервал времени t. При этом оказывается, что одномерная функция распределения, математическое ожидание и дисперсия вообще не зависят от времени: а двухмерная функция распределения и корреляционная функция, и ковариационная функция зависят только от расстояния между сечениями

Иногда случайный процесс называют стационарным в широком смысле, если приведенные условия выполняются лишь для числовых характеристик. Узкое и широкое определения стационарности не тождественны. Случайные процессы, стационарные в узком смысле, всегда стационарны в широком смысле, но не наоборот.

Если приведенные выше условия не выполняются, то случайный процесс будет нестационарным. Для нестационарного процесса плотность вероятности является функцией времени. При этом со временем могут изменяться математическое ожидание, дисперсия случайного процесса или то и другое вместе.

Среди стационарных случайных процессов очень важное значение имеют так называемые эргодические процессы, для которых статистические характеристики можно найти усреднением не только по ансамблю реализации, но и по времени одной реализации продолжительностью Т. При этом числовые характеристики, полученные по одной реализации путем усреднения по времени, с вероятностью, сколь угодно близкой к единице, совпадают с соответствующими числовыми характеристиками, полученными путем усреднения по множеству (ансамблю) реализации в один момент времени. Следовательно, для эргодических процессов:

Операция усреднения по времени одной реализации обозначается волнистой линией сверху.

Существует теорема, согласно которой стационарные в узком смысле процессы при достаточно общих предположениях являются эргодическими.

Свойство эргодичности стационарных случайных процессов имеет большое практическое значение. Для таких процессов любая реализация полностью определяет свойства всего процесса в целом. Это позволяет при определении статистических характеристик случайного процесса ограничиться рассмотрением лишь одной реализации достаточно большой длительности, как это и делается в настоящей лабораторной работе при определении одномерной плотности вероятности.

У любого случайного процесса следует различать кроме мгновенных значений и максимальные значения, которые также являются случайными величинами и характеризуются своими законами распределения. Огибающая случайного процесса определяется как геометрическое место точек, соответствующих максимальным значениям процесса, и обозначается E(t) с плотностью распределения вероятностей W(E).

Остановимся коротко на методике практического измерения временных характеристик случайных процессов.

Математическое ожидание (постоянная составляющая) эргодического случайного процесса определяется выражением. Следовательно, измерение должно сводиться к достаточно длительному интегрированию реализации процесса и умножению на величину 1/Т. Очень часто операция интегрирования (т.е. усреднения по времени) осуществляется с помощью фильтров нижних частот и в частности, интегрирующих RC – цепочек.

Для измерения полной мощности эргодического случайного процесса в соответствии с выражением необходимо осуществить операции возведения в квадрат исследуемого процесса и интегрирования.

Для случайного процесса с ненулевым математическим ожиданием дисперсия (мощность переменной составляющей) равна.

В соответствии с этим выражением при измерении полной мощности случайного процесса можно исключить постоянную составляющую и тем самым упростить измерение.

Для измерения ковариационной функции случайного процесса К(?) необходимо осуществить операции задержки на различное время ? , умножения и интегрирования. Обычно ограничиваются измерением В(?) в нескольких точках. При этом необходимо располагать набором перемножителей и линий задержки на фиксированное время задержки (чаще всего используют линию задержки с отводами).

Определение одномерной функции распределения вероятностей случайных процессов.

Для эргодических случайных процессов по одной реализации могут быть определены не только числовые характеристики, но и функция распределения вероятностей Р(?) или плотность распределения вероятностей W(x). Функция распределения Р(х) определяется как относительное время пребывания одной реализацию длительностью Т (интервал наблюдения) ниже уровня x.

Соответственно плотность вероятности равна

Таким образом, аппаратурное определение функции распределения эргодического процесса по одной реализации основано на измерении относительного времени пребывания случайного напряжения в интервале значений от U до (U + ?U).

При реальных U измеряется вероятность

ля различных U и строится распределение вероятностей в виде гистограммы. Для получения функции плотности вероятностей W(U) необходимо аппроксимировать гистограмму непрерывной кривой или ожидаемым законом распределения, пользуясь критериями согласия.

Метод статистических испытаний

Определение 1.   Метод вычисления некоторой детерминированной величины a как среднего арифметического Yn независимыхСВXn с одинаковым распределением, подобранным таким образом, чтобы

Yn

п.н.→

a,

называется методом статистических испытаний (методом Монте-Карло) для вычисления a.

Замечание 1.   В некоторых учебниках метод Монте-Карлоназывают также методом статистического моделирования, что, на наш взгляд, не совсем корректно. Дело в том, что термин "моделирование'' используется также в теории математического моделирования для описания процесса создания математических моделей каких-либо явлений. Подчеркнем, что в методе Монте-Карло речь идет о статистической имитации испытаний (опытов), а не о процессе создания статистических моделей опытов. Оправдано говорить лишь о моделировании случайных величин, если используются, например, датчики случайных чисел.

Замечание 2.   Метод Монте-Карло имеет огромную область приложений. Наиболее трудной проблемой в его реализации является выбор необходимого числа испытаний n такого, чтобы можно было считать, что СВYn достаточно "близка" к a. Ясно, что из-за вычислительных трудностей желательно выбирать величину n с возможно меньшим гарантирующим значением N. Для выбора N обычно используютцентральную предельную теорему, считая, что распределение нормированной суммы ZNСВXk, k = 1,N, являетсястандартным нормальным распределениемN(0,1). Рассмотрим на примерах, как выбирается величина N.

Пример 1.   Рассмотрим применение метода статистических испытаний для оценивания неизвестной вероятности

p

Δ =

P(A)

некоторого события A. В соответствии с теоремой Бернулли

M / n

п.н.→

p ,.

а в соответствии с теоремой Муавра - Лапласа

* Wn = Zn

Δ =

M-np √npq

F→

U, где U ~ N(0,1).

Воспользуемся этими теоремами для выбора гарантирующего числа испытаний N, при котором можно было бы сказать, что СВM / N "близка" к оцениваемой вероятности p. Поступим аналогично тому, как выбиралось Nβ в примере2из предыдущего раздела. Вначале зададим точность Δ оценки вероятности p: |M/n - p| ≤ Δ. Затем найдем надежность этой оценки, учитывая, что

* Wn = Zn ≈ U,

P

{

|

M  n

- p| ≤ Δ

}

= P

{

M-np √npq

≤ Δ

√

n   pq

}

≈ 2Φ0

(

Δ

√

n   pq

)

.

Задав доверительную вероятность β, получим трансцендентное уравнение: 2Φ0(Δ√N/pq) = β , из которого можно найти

Nβ =

[

(xβ/2)2p(1-p)         Δ2

]

+ 1,

, где Φ0(xβ/2) = β/2. Но величины p и q = 1 - p заранее неизвестны, поэтому заменим величину p(1 - p) на ее максимальное значение, которое, очевидно, достигается при p = 1/2 и равно 1/4. Поэтому выбираем Nβ = [(xβ/2)2/(2Δ2)] + 1. В этом примере для вычисления Nβ необходимо задать уровень доверительной вероятности β (вторичный по отношению к p) и точность Δ вычисления p. Например, при p > 0.8 обычно задают Δ = (1-p)/10 и β = 1-Δ.