Дисперсией случайной величины называется число

то есть дисперсия есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания. Число называется среднеквадратичным отклонением, поэтому дисперсия часто обозначается σ².

Свойства дисперсии следуют из ее определения и свойств математического ожидания.

1⁰. D[С]=0, если С - неслучайная величина.

2⁰. М[С X] = С^{2 .} М[Х], если С - неслучайная величина.

3⁰. D[XY] = D[X]+D[Y]. если случайные величины Х и Y независимы

4⁰. D[X] = M[X²] – (M[X])² = M[X²] – m²

Приведем формулы вычисления дисперсии для дискретных случайных величин:

где m=М|Х] - математическое ожидание, рассчитываемое предварительно по формулам

Функция распределения. Плотность распределения и числовые характеристики непрерывной случайной величины М(Х), Д(Х),.

Функцией распределения случайной величины Х называется функция F(х), равная вероятности того, что Х примет значение меньше, чем число х, то есть F(х)=F(Х<х). Иногда ее называют интегральной функцией распределения.

Рассмотрим свойства функции распределения.

1⁰. 0≤F(x)≤1.

2⁰. F(х) - неубывающая функция, т. е. из х₂>х₁ следует F(х₂)≥ F(х₁).

3⁰ . Р(х1≤Х<x₂) =F(х₂)-F(х₁), если х₂>x₁.

4⁰. Р(х) непрерывна слева, то есть для любой точки x₀

5⁰. .

6⁰. Если F(х) непрерывна в точке x₀ , то Р(Х=x₀) = 0.

Если функцию распределения F(х) непрерывной случайной величины можно представить в виде то функция f(x) называется плотностью распределения вероятности.

Свойства плотности распределения.

1⁰. f(x)≥0 .

2⁰. .

ПРИМЕР . Равномерное распределение. Говорят, что случайная величинаХравномерно распределена на отрезке[a,b], если она имеет следующую плотность:

Значение постоянной с определяем из условия нормировки

,

откуда .

График плотности распределения приведен на рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной величины Х равна

.

Поэтому можно сказать, что вероятность попадания равномерно распределенной случайной величины на какой-либо отрезок пропорциональна длине этого отрезка и не зависит от его положения внутри области возможных значений.

Построим теперь функцию распределения. При х<афункция распределения равна нулю, так какf(х)=0. При а≤x≤bполучаем

.

Для x>b получаем

.

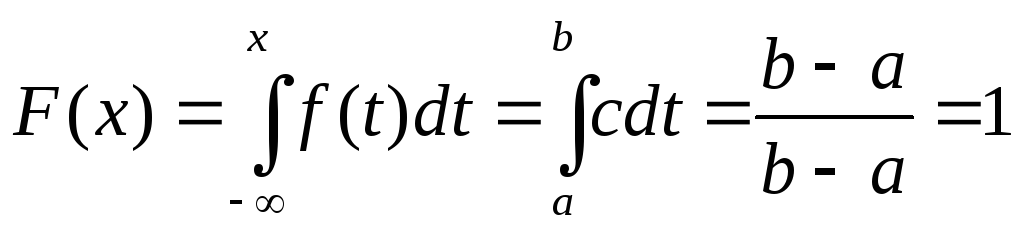
Таким образом,

График функции распределения приведен на рис.12.

С равномерно распределенными случайными величинами мы сталкиваемся тогда, когда по условиям опыта случайная величина принимает значения на некотором конечном промежутке, причем все возможные значения из этого промежутка равновозможны. Например, Х - время ожидания на остановке автобуса - равномерно распределен­ная на отрезке [0,Т]случайная величина, где Т - интервал движения автобусов по расписанию.

ПРИМЕР. Нормальное распределение Гаусса. 1/σ√2π

,

гдеm – любое действительное число, а σ - любое положительное действительное число. Эти числа называются параметрами распределения. Нормальный закон распределения зависит, таким образом, от двух параметров. График плотности распределения имеет вид, приведенный на рис.13.

Если m=0 и σ =1, то нормальный закон распределения называется стандартным и имеет плотность

Однако далеко не во всякой задаче нам необходимо знать закон распределения случайной величины полностью. В ряде случаев можно обойтись несколькими числами, отражающими наиболее важные особенности закона распределения интересующей нас случайной величины. Например, числом, характеризующим среднее значение случайной величины, и числом, характеризующим средний размах отклонения случайной величины от своего среднего значения и т.п. Такого рода числа называются числовыми характеристиками случайных величин.

При переходе к непрерывным случайным величинам суммирование заменяется интегрированием. Поясним подробней. Разобьем множество возможных значений непрерывной случайной величины точками х₁,х₂,...,х_n на небольшие отрезки длин ∆x_k = x_k – x_k-1 (k=2,3,…n).

Тогда по свойству 2 плотности распределения и теореме о среднем для определенного интеграла получаем

,

где f(х) - плотность распределения случайной величины, а точка Мы заменяем приближенно нашу непрерывную случайную величину дискретной с законом распределения Р(Х=ξ_k)=р_k. Поэтому

это интегральная сумма. Осталось перейти к пределу при и получить соответствующий интеграл.

Математическим ожиданием или средним значением непрерывной случайной величины, заданной своей плотностью распределения f(х), называется число

ПРИМЕР 3. Для равномерного на отрезке [а,b] распределения имеем

;

;

и т.д.

Приведем формулы вычисления дисперсии для непрерывных случайных величин:

,

где m=М|Х] - математическое ожидание, рассчитываемое предварительно по формулам

Нормальный закон распределения. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Функция Лапласа.

По определению плотность нормально распределенной случайной величины равна

Возможные значения такой величины Х могут принимать любые действительные значения -∞<Х<∞, а распределение зависит от двух параметров . -∞<m<∞ и -∞<σ<∞.

Таким образом, график функции f(х) будет таким:

П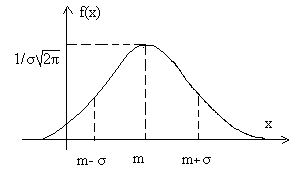ри измененииm кривая f(x) скользит вдоль оси абсцисс, не меняя своей формы. При изменении σ кривая меняет свою форму: если σ увеличивается, то кривая становится ниже и шире и наоборот.

 

 

 

 

Если m=0 и σ=1, то закон нормального распределения называется стандартным. В этом случае

Если случайная величина Х распределена по нормальному закону с параметрами m и σ , то этот факт записывают так:.

Вычислим математическое ожидание случайной величины

Таким образом, параметр m - это математическое ожидание случайной величины X.

Вычислим теперь дисперсию

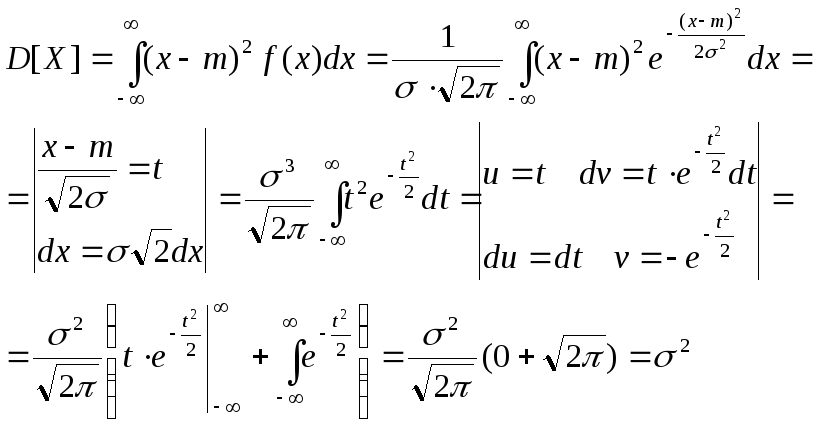
где мы использовали то, что по правилу Лопиталя

Таким образом, параметр σ - это среднеквадратическое отклонение, поскольку σ²- это дисперсия.

Мода и медиана нормального распределения совпадает с математическим ожиданием, т.к. максимум f(x) достигается при x=m и

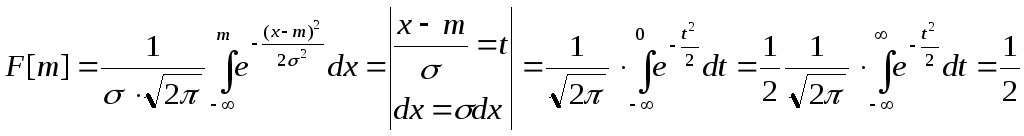
где

функция распределения закона которая имеет график, представленный на рисунке.

Пусть Вычислим Р(а<Х<b) - вероятность попадания нормально распределенной случайной величины в заданный интервал. По свойству плотности распределения имеем

где мы использовали формулу Ньютона-Лейбница для определенных интегралов, а - любая первообразная для подынтегральной функции

Любая первообразная может быть рассчитана по формуле

где С- произвольная постоянная. Это можно легко проверить диффе­ренцированием .

При С=0 мы получаем функцию Лапласа

а при С=∞ - функцию распределения стандартного нормального закона

Нетрудно получить связь между Ф*(х) и Ф(х).

Окончательно получаем

В зависимости от имеющихся у нас под руками таблиц мы воспользуемся той или иной формулой. Отметим, что пользоваться таблицами функции Лапласа удобней, так как она нечетна и мы легко - находим ее значения при отрицательном аргументе (обычно, таблицы заданы только для положительных значений аргумента). Пользоваться таблицами функции Ф*(х) в этом случае несколько неудобнее, если она задана только для положительных значений аргумента.

ПРИМЕР 1. Пусть Найдем вероятность того, что Х примет значение из интервала ]0;3[.

По таблице функции Лапласа получаем

По таблице функции распределения стандартного нормального закона получаем, используя ее связь с функцией Лапласа:

Вэтом примере мы вывели полезную формулу

Ф^*(-х)=1-Ф^*(х),

которую легко пояс­нить следующим рисунком.

Найдем вероятность попадания нормальной случайной величины в интервал ]m-l,m+l[, симметричный относительно математического ожидания:

При различных l получаем

Как мы видим, хотя теоретически возможные значения Х могут быть любые, но практически все значения попадают в интервал ]m-3σ,m+3σ[. Этот факт обычно называют правилом «трех сигм». При нормальном распределении из 10000 измерений только 27 имеют «законное» право выйти из этого интервала ( событие маловероятное и им обычно пренебрегают). Поэтому можно считать, что все воз­можные значения нормальной случайной величины находятся в этом интервале.

 

Распределение монотонной функции случайной величины. Исследование системы двух случайных величин. Функциональная и вероятностная зависимость. Условная плотность.

Часто приходится рассматривать сразу несколько случайных величин одновременно. Например, при стрельбе по мишени точка попадания имеет две координаты, которые являются случайными величинами; при медицинском осмотре основными параметрами состояния здоровья считаются частота пульса, уровень кровяного давления, температура тела и т.д., которые при случайном выборе человека являются случайными величинами.

Пусть Х и Y - дискретные случайные величины. Двумерная случайная величина {X, Y} называется системой дискретного типа и задается следующей таблицей, называемой двумерным рядом распределения

Y X	У1	У2	Уз	…	Уj	...
x1	Р11	P12	P13	…	P1j	...
x2	P21	P22	P23	...	P2j	…
…	…	...	...	…	…	…
xi	Pi1	Pi2	Pi3	...	Pij	...
…	…	…	…	…

 где Pij=(X=xi;Y=yj).