5. Классическое определение вероятности, статистическая вероятность. Зависимые и независимые события теоремы сложения и умножения вероятности. Формула полной вероятности, формула Байеса.

Любая точная наука изучает не сами явления, протекающие в природе, в обществе, а их математические модели, т. е. описание явлений при помощи набора строго определенных символов и операций над ними. При этом для построения математической модели реального явле­ния во многих случаях достаточно учитывать только основные факторы, закономерности, которые позволяют предвидеть результат опы­та (наблюдения, эксперимента) по его заданным начальным условиям.

Однако есть множество задач, для решения которых приходится учитывать и случайные факторы, придающие исходу опыта элемент неопределенности. Например, в вопросах стрельбы по цели невозможно без учета случайных факторов ответить на вопрос: сколько ракет нужно потратить для поражения цели? Невозможно предсказать, какая сторона выпадет при бросании монеты. Сколько лет проживет родившийся сегодня ребенок? Такие задачи, исход которых нельзя предсказать с полной уверенностью, требуют изучения не только основных, главных закономерностей, определяющих явление в общих чертах, но и случайных, второстепенных факторов. Выявленные в таких задачах (опытах) закономерности называются статистическими (или вероятностными). Статистические закономерности исследуются методами специальных математических дисциплин - теории вероятностей математической статистики.

Теория вероятностей - математическая наука, изучающая закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. То есть теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы - математические модели. Предметом теории вероятностей являются математические модели случайных явлений. При этом под случайным явлением понимают явление, предсказать исход которого невозможно (при неоднократном воспроизведении одного и того же опыта оно протекает каждый раз несколько по-иному).

Примеры случайных явлений: выпадение герба при подбрасывании монеты, результат измерения какой-либо величины, длительность работы телевизора и т. п..

Цель теории вероятностей - осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы действия случайности. В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы.

Случайным событием (или просто: событием) называется любой исход опыта, который может произойти или не произойти.

События обозначаются, как правило, заглавными буквами латинского алфавита: А, В, ... .

Пример. Опыт: бросание игральной кости; событие А - выпадение 5 очков, событие В - выпадение четного числа очков, событие С - выпадение 7 очков, событие D - выпадение целого числа очков, событие Е - выпадение не менее 3-х очков, ....

Непосредственные исходы опыта называются элементарными событиями и обозначаются через W. Элементарные события (их называют также «элементами», «точками», «случаями») рассматриваются как неразложимые и взаимоисключающие исходы Wl, W2, Wз ... этого опыта.

Множество всех элементарных событий называется пространством элементарных событий или пространством исходов, обозначается через П.

Рассмотрим пример 1.1. Здесь 6 элементарных событий W_l, W₂, Wз, W₄, W₅, W₆. Событие Wi означает, что в результате бросания кости выпало i очков, i = 1,2,3,4,5,6. Пространство элементарных событий таково: n = {W_l,W₂,W_З,W₄,W₅,W₆} или n = {1,2,3,4,5,6}.

Событие называется достоверным если оно обязательно наступит в результате данного опыта.

Событие называется невозможным если оно заведомо не произойдет в результате проведения опыта.

Два события называются несовместными если появление одного из них исключает появление другого события в одном и том же опыте, т. е. не смогут произойти вместе в одном опыте. В противном случае события называются совместными.

События А₁, А₂, ..., А_п называются попарно несовместными, если любые два из них несовместны.

Несколько событий образуют полную группу, если они попарно не­совместны и в результате каждого опыта происходит одно и толькоодно из них.

Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие, т. е. все события имеют равные «шансы».

Суммой событий А и В называется событие С = А + В, состоящее в наступлении хотя бы одного из них (т. е. или А, или В, или А и В вместе) .

Произведением событий А и В называется событие С = А*В, состоящее в совместном наступлении этих событий (т. е. и А и В одновременно) .

Разностью событий А и В называется событие С = А - В, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В.

Противоположными событию А называется событие , которое происходит тогда и только тогда, когда не происходит событие А.

Случайным событием А (или просто событием А) называется любое подмножество множества О, если О конечно или счетно (т. е. элементы этого множества можно пронумеровать с помощью множества натуральных чисел): А ~ О.

Элементарные события, входящие в подмножество А пространства О, называются благоnриятствующими событию А.

Множество О называется достоверным событием. Ему благоприятствует любое элементарное событие; в результате опыта оно обяза­тельно произойдет.

Пусть в n повторяющихся опытах некоторое событие А настуnuло т раз.

Число т называется частотой, события А, а отношение

называется относuтелъной частотой события А в рассматриваемой серии опытов.

Для математического изучения случайного события необходимо ввести какую-либо количественную оценку события. Понятно, что одни события имеют больше шансов «более вероятны») наступить, чем другие. Рассмотрим опыт, который можно повторять любое число раз (говорят: «проводятся повторные испытания»), в котором наблюдается некоторое событие А.

Статuстической вероятностъю события А называется число, около которого колеблется относительная частота события А при достаточно большом числе испытаний (опытов).

Вероятность события А обозначается символом Р(А). Согласно данному определению

Математическим обоснованием близости относительной частоты и вероятности некоторого события А служит теорема Я. Бернулли.

Вероятности Р(А) приписываются свойства 1-4 относительной частоты:

1. Статистическая вероятность любого события заключена между нулем и единицей.

2.Статистическая вероятность невозможного события равна нулю.

3.Статистическая вероятность достоверного события равна единице.

4. Статистическая вероятность суммы несовместных событий равна сумме вероятностей этих событий.

Существует простой способ определения вероятности события, основанный на равновозможности любого из конечного числа исходов опыта. Пусть проводится опыт n исходами, которые можно предста­вить в виде полной группы несовместных равновозможных событий. Такие исходы называются случаями, шансами, элементарными событиями, опыт - классическим. Про такой опыт говорят, что он сводится к схеме случаев или схеме урн.

Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев, т. е.

Наряду с обозначением Р(А) для вероятности события А используется обозначение р, т. е. р = Р(А).

Из классического определения вероятности вытекают следу­ющие свойства:

1. Вероятность любого события заключена между нулем и единицей.

2. Вероятность невозможного события равна нулю.

3. Вероятность достоверного события равна единице.

4. Вероятность суммы несовместных событий равна сумме вероятно­стей этих событий

Пример В урне (емкости) находятся 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?

Пусть А - событие, состоящее в том, что вынут белый шар. Яс­но, что n = 12 + 8 = 20 - число всех равновозможных случаев (исхо­дов опыта). Число случаев, благоприятствующих событию А, равно 12,

т. е. m = 12. Следовательно, по формуле (1.3) имеем: Р(А) = т. е.

Р(А) = 0,6. .

Комбинаторика - раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества. В каждой из них требуется подсчитать число возможных вариантов осуществления не которого действия, ответить на вопрос «сколькими способами?».

Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно nравилами умножения и сложения.

Правило умножения (основной принцип): если из некоторого конечного множества первый объект (элемент х) можно выбрать п₁ способами и после каждого такого выбора второй объект (элемент у) можно выбрать п₂ способами, то оба объекта (х и у) в указанном порядке можно выбрать п₁ *п₂ способами.

Этот принцип, очевидно, распространяется на случай трех и более объектов.

Правило суммы. Если некоторый объект х можно выбрать n_l способами, а объект у можно выбрать п₂ способами, причем первые и вторые способы не пересекаются, то любой из указанных объектов (х или у), можно выбрать п₁ + п₂ способами.

Это правило распространяется на любое конечное число объектов.

Решение вероятностных (и не только их) задач часто облегчается, если использовать комбинаторные формулы. Каждая из них определяет число всевозможных исходов в некотором опыте (эксперименте), состоящем в выборе наудачу m элементов из п различных элементов рассматриваемого множества.

Существуют две схемы выбора m элементов (о < m п) из исходного множества: без возвращения (без повторений) и с возвращением (с повторением). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все m элементов или последовательно отбирать их по одному. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.

Схема выбора без возвращений

Пусть дано множество, состоящее из п различных элементов. Размещением из п элементов по m элементов (о < m п) называется любое упорядоченное подмножество данного множества, содержащее m элементов.

Из определения вытекает, что размещения - это выборки (комбинации), состоящие из m элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения. I

Число, размещений из п элементов по m элементов обозначается символом вычисляется по формуле=, гдеп! = 1 . 2 . 3 . . . . . п, 1! = 1, о! = 1.

Пример Составить различные размещения по 2 из элементов мно­жества D = {а, b, с}; подсчитать их число.

Из трех элементов можно образовать следующие размещения по два элемента: (а, b), (b, а), (а, с), (с, а), (b, с), (с, b). Согласно формуле (1.4) их число: = 3 * 2 = 6. .

Перестановкой из n элементов называется размещение из n эле­ментов по n элементов.

Из определения вытекает, что перестановки - это выборки (комбинации), состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов. Число перестановок из n элементов обозначается символом и вычисляется по формуле

=n!

Пример. Составить различные перестановки из элементов мно­жества Е = {2, 7, 8}; подсчитать их число.

Из элементов данного множества можно составить следующие пе­рестановки: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). По формуле (1.6) имеем: Р_З == 3! = 1 *2 *3 = 6. .

Пример 1.11. Сколькими способами можно расставить на полке 5 различных книг?

Искомое число способов равно числу перестановок из 5 элементов

(книг), т. е. Р₅ = 5! = 1*2*3*4*5 = 120.

Сочетанuем из n элементов по m элементов называется любое подмножество, которое содержит m элементов данного множества.

Из определения вытекает, что сочетания - это выборки (комбинации), каждая из которых состоит из m элементов, взятых из данных n элементов, и которые отличаются друг от друга хотя бы одним эле­ментом, т. е. отличаются только составом элементов.

Число сочетаний из n элементов по m элементов обозначается сим­волом и вычисляется по формуле

Су.ммой А + В двух событий А и В – называют событие, состоящее в появлении события А, или события В, или обоих этих событий.

Например, если из орудия произведены два выстрела и А - попадание при пером выстреле, В - попадание при втором выстреле. То А+ В - попадание при первом выстреле, или при втором, или В обоих выстрелах.

В частности, если два события А и В – несовместные, то А + В-событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме веро­ятностей этих событий:

Р(А+В)=Р (А)+Р(В).

Следствие. Вероятность появления одного из нeскольких попарно нecoвмecmных событий, безразлично, какого, равна сумме вероятностей этих событий:

Р (А₁ + А₂ + . . . + А_n) = Р (А₁) + P (А₂) + . . . + Р (A_n).

Пример 1. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую- 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Решение. События А - «стрелок попал в первую область» и В - «стрелок попал во вторую область» - несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.

Искомая вероятность

Р (А+В)=Р (А) +Р (B)=0,45+0,35=0,80.

Теорема. Сумма вероятностей событий А₁, А₂,…., А_п, образующих полную группу, равна единице: Р (А₁) + Р (А₂) + . . . + Р (А_п) = 1.

Пример. Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В - О,2. Найти веро­ятность того, что очередной пакет будет получен из города С.

Решение. События «пакет получен из гopoда А», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице: 0,7+0,2+p=1.Отсюда искомая вероятность p=0,I.

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .

Пример. Попадание и промах при выстреле по цели - противоположные события. Если А-попадание, то -промах.

Теорема. Сумма вероятностей противоположных событий равна единице.

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А-деталь годная, В-деталь окрашенная, то АВ - деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С-появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС выпадение «герба» во всех трех испытаниях.

Условной вероятностью Р _А (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров из них 3 белых. Искомая условная вероятность Р _А (В) =3/5.

Этот же результат можно получить по формуле

Р_А (В)=Р (АВ)/Р (А) (*)

Рассмотрим два события: А и В; пусть вероятности Р(А) и Р _А (В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В. Ответ на этот вопрос дает теорема умножения.

Теорема. Вероятность совместного появления двух событий равна nпроизведению вероятности одного из них на условную вероятность другого, вычисленную в nредnоложении,. что первое событие уже наступило:

Р (АВ) = Р (А) Р _А (В).

С л е дс т в и е. Вероятность совместного появления нескольких событий равна nпроизведению вероятности одного из них на условные вероятности всех остальных, nпричем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

В частности, для трех событий

Р(АВС) = Р (А) Р _А (В) Р _АВ (С).

3аметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д.

Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков-конусный, а второй эллиптический.

Решение. Вероятность того, что первый валик окажется конусным (событие А).

Р (А) =3/10.

Вероятность того, что второй валик окажется эллиптическим (событие В) вычисленная в предположении, что первый валик конусный, т. е. условная вероятность

Р _А (В) = 7/9.

По теореме умножения, искомая вероятность

Р (АВ) =Р (А) Р _А (В) =(3/10)*(7/9)=7/30.

Пусть вероятность события В не зависит от появления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В т. е. если условная вероятность события В равна безусловной вероятности:

Р _А (В) = Р (В).

Для независимых событий теорема умножения имеет вид

Р (АВ) = Р (А) Р (В), т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависи­мыми.

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

Пример. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8. а вторым (событие В)-0,7.

Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность

Р (АВ) = Р (А) Р (В) = 0,7*0,8 = 0,56.

Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.

Несколько событий называют независимыми в совокупности (или просто незавucимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Р(А₁, А₂, …А_n)= P(A₁) P(A₂)…P(A_n)

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в часности только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий А₁ , А₂ ..., А_n, независимых в coвoкупности, равна разности между единицей и произведением вероятностей противоположных событий:

P(A)=I-q_lq₂ ... q_n. (*)

Частный случай. Если события А₁ , А₂ ..., А_n имеют одинаковую вероятность, равную р, то вероят­ность появления хотя бы одного из этих событий

Р (А) = l-qⁿ.

Пример 1. Вероятности попадания в цель при стрельбе из трех орудий таковы: р₁=0,8; р₂=0,7; р_з=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события А₁ (попадание первого орудия), А₂ (попадание второго орудия) и А_з (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям А₁, А₂ и А₃.

(т. е. вероятности промахов), соответственно равны:

q₁= l - р_l= 1-0,8=0,2; q₂= 1 – p₂= 1-0,7=0,3;

q₃= l-р_з= 1-0,9=0,1.

Искомая вероятность

Р (А) = 1 -q₁q₂q_з= 1-0,2*0,3*0,1 =0,994.

Была рассмотрена теорема сложения ля несовместных событий. Здесь будет изложена теорема сложения для совместных событий.

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример 1. А-появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В совместны.

Пусть события А и В совместны, причем даны вероятности этих событий и вероятности их совместного появления. Как найти вероятность события А+В, состоящего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий.

Теорема Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р (А + В) = Р (А) + Р (В) - Р (АВ).

Формула полной вероятности

Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂, …В_n, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности событияА. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, …В_n, образующих полную группу, равна сумме nроизведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р (А) =

Эту формулу называют «формулой полной вероятности».

Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго -0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) - стандартная.

Решение. Обозначим через А событие «извлеченная деталь стандартна».

Деталь можeт быть извлечена либо из первого набора (событие В₁) либо из второго (событие В₂). .

Вероятность того, что деталь вынута из первого набора, Р (В₁ )=1/2. . .

Вероятность того, что деталь вынута из второго набора, Р (В₂)= 1/2.

Условная вероятность того, что из первого набора будет извле­чена стандартная деталь,

(А) =0,8.

Условная вероятность того, что из второго набора будет извлечена стандартная деталь,

(А) =0,9.

Искомая вероятность того, что извлеченная наудачу деталь - стандартная, по формуле полной вероятности равна

Р (А) = = 0,5*0,8 + 0,5*0,9 = 0,85.

Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂, …В_n, образующих полную группу. Поскольку заранее не из­вестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности

Р (А) =

Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

Найдем сначала условную вероятность По теореме умножения имеем

Р(АВ₁)=Р(А) Р_А(В₁)=Р(В₁)

Отсюда

Заменим здесь Р(А) формулой полной вероятности, получим

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы В_i (i=1, 2, …n) может быть вычислена по формуле

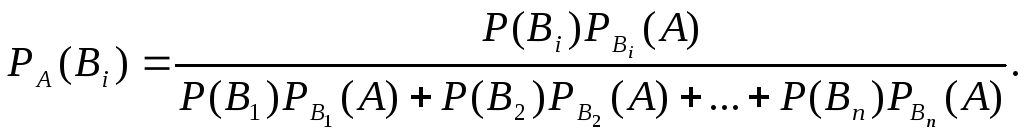
Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 го). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого nоявuлось событuе А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Веро­ятность того, что деталь попадает к первому контролеру равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером равна 0,94, а вторым - 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность тoгo, что эту деталь проверил первый контролер.

Р е ш е н и е. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:

1) деталь проверил первый контролер (гипотеза В₁);

2) деталь проверил второй контролер (гипотеза В₂).

Искомую вероятность того, что деталь проверил первый контролер найдем по формуле Бейеса:

По условию задачи имеем:

Р (В₁) = 0,6 (вероятность того, что деталь попадает к первому конт­ролеру);

Р (В₂) = 0,4 (вероятность того, что деталь попадет ко второму контролеру);

(А)=0,94 (вероятность того, что годная деталь будет признана первым контролером стандартной);

(А)=0,98 (вероятность того, что годная деталь будет признана вторым контролером стандартной).

Искомая вероятность

Р А (В₁) = (0,6*0,94)/(0,6*0,94+0,4*0,98) 0,59.

Случайная величина и закон ее распределения. Числовые характеристики дискретной случайной величины М(Х), Д(Х),. Формула Бернулли.

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.

Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность не наступления события А в каждом испытании также постоянна и равна q= 1-p.

Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится n-k раз. Важно подчеркнуть, что не требуется чтобы событие А повторилось ровно k раз в определенной последовательности.

Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n – k раз, можно вычислить используя формулу

Или

Полученную формулу называют формулой Бернулли.

Пример. Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна p=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии в продолжении каждые из 6 суток постоянна и равна р=0,75. следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q=1-p=1-0,75=0,25.

Искомая вероятность по формуле Бернулли равна

Р₆(4)==

Локальная теорема Лапласа

Выше была выведена формула Бернулли позволяющая вычислить вероятность того, что событие появится в n испытаниях ровно k раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то верояmность Р _п (k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции

при

Имеются таблицы, в которых помещены значения функции , соответствующие положительным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция четна, т. е. (-x)=(x).

Итак, вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна

где

Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р _n (k₁, k₂) того, что событие А появится в п испытаниях от k₁, до k₂ раз, приближенно равна определенному интегралу

где

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл не

выражается через элементарные функции. Таблица для интеграла Ф (х) = 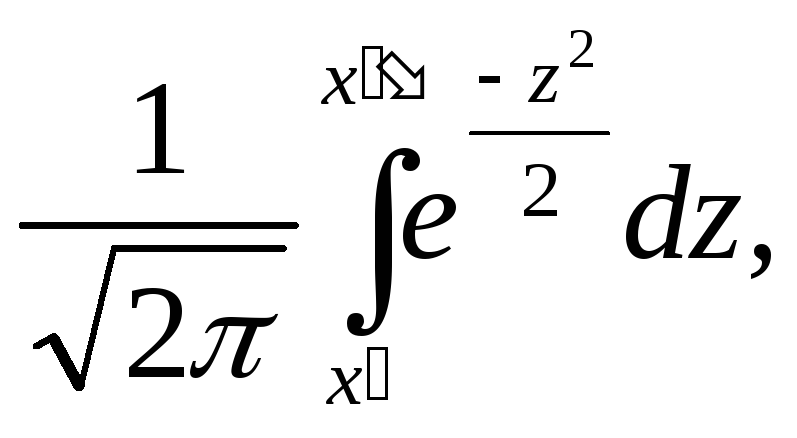приведена (см. приложение 2). В таблице даны значения функции Ф (х) для положительных значений х и для х = о; для х < О пользуются той же таблицей [функция Ф (х) нечетна. т. е. Ф (- х) = - Ф (х). В таблице приведены значения интеграла лишь до х = 5. так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф (х) часто называют функцией Лапласа.

Для того чтобы можно было пользоваться таблицей функции Лапласа, формулу преобразуем к виду:

где

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р =0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию, р=0,2; q=0,8; п=400; k₁=70; k₂ = 100. Воспользуемся интегральной теоремой Лапласа:

Вычислим нижний и верхний пределы интегрирования:

Таким образом, имеем ,

Р₄₀₀(70, l00)= Ф (2,5)-Ф (-1,25)=Ф(2,5)+Ф (1,25).

По таблице приложения 2 находим:

Ф (2,5) =0,4938; Ф (1,25) =0,3944.

Искомая вероятность

Р₄₀₀ (70, 100)=0,4938+0,3944=0,8882.

Случайной величиной называется величина, которая в результате опыта может принять какое-либо числовое значение, заранее нам неизвестное. Все это множество, называемое множеством возможных значений случайной величины, нам заранее известно.

По типу множества возможных значений случайные величины бывают двух видов - дискретные и непрерывные. Случайные величины, как и случайные события, мы будем обозначать заглавными буквами.

Для случайных величин возникает задача: вычислить вероятности того, что они будут принимать те или иные значения из множеств своих возможных значений.

Законом распределения случайной величины называется любое правило, позволяющее для произвольного набора возможных значений вычислять соответствующие вероятности.

Закон распределения может быть выражен в различных формах.

Множества называются эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие.

Множество называется счетным, если оно эквивалентно множеству натуральных чисел N={1,2,3,...,n,...} (его элементы можно пронумеровать).

Случайная величина называется дискретной, если множество ее возможных значений - конечное или счетное числовое множество.

Пусть Х₁,Х₂,...- возможные значения случайной величины, а p₁,p₂,… - соответствующие вероятности, то есть

p_i=P(X=x_i), i=1,2,…

Тогда можно составить таблицу вида

Значения Х	x1	x2	…
Вероятности  Р	p1	p2	…

которая называется рядом распределения дискретной случайной величины и является одной из форм закона распределения. Случайные события (Х=хi) попарно несовместны и в совокупности образуют полную группу, поэтому из теоремы сложения вероятностей не­совместных событий мы получаем

.

Этим свойством обязан обладать любой ряд распределения. Обозначение (i) здесь означает суммирование по всем возможным значениям. Для конечного множества возможных значений это будет конечная сумма, для счетного - сходящийся числовой ряд.

ПРИМЕР. Монета бросается 3 раза. Х - число выпавших гербов. Тогда множество возможных значений {0, 1, 2, 3}, а соответствующие вероятности подсчитываются по формуле Бернулли при n=3 и p=q=1/2;

Соответствующий ряд распределения

Х	0	1	2	3
Р	1/8	3/8	3/8	1/8

 В последнем примере вероятности подсчитывались по формуле вида

pi=P(X=xi)=φ(xi).

Это другая форма закона распределения случайной величины. Будем говорить «закон задан с помощью формулы».

ПРИМЕР Пусть имеется схема Бернулли с n испытаниями и вероятностью успеха р в одном испытании. Х - общее число успехов в n испытаниях. Тогда ряд распределения будет выглядеть следующим образом:

Х	0	1	2	…	n
Р	Pn(0)	Pn(1)	Pn(2)	…	Pn(n)

 

где вероятности рассчитываются по формуле Бернулли .

Закон распределения, заданный с помощью формулы Бернулли, называется биномиальным.

Закон распределения, заданный с помощью формулы Пуассона, называется распределением Пуассона.

В этом случае число успехов Х принимает значения из бесконечного счетного множества {0,1, 2,...}.

Закон распределения дискретной случайной величины можно представить графически, изображая в декартовой системе координат вероятность рi и в зависимости от возможных значений хi. Для боль­шей наглядности полученные точки соединяются отрезками прямых. Эта форма закона распределения называется многоугольником распределения.

В тех случаях, кода число испытаний n велико, а вероятность р (или q) мала, неравенство npq>>1 не выполняется, следовательно, в этих случаях пользоваться формулой Бернулли практически невозможно, а теоремы Лапласа дают очень большую ошибку.

.

Это и есть формула редких событий Пуассона.

Наиболее важной характеристикой случайной величины является ее среднее значение.

Предположим, что случайная величина Х связана с некоторым опытом и пусть проведено всего N опытов. При этом значение х₁ мы наблюдали N₁ раз, значение х₂–N₂ раз и т.д. Найдем среднее арифметическое всех значений:

,

где N_i/N- относительная частота появления значения х_i (i=1,2,...). Мы уже знаем, что при N→∞ эта величина стремится к вероятности р_i случайного события (Х=х_i), что отмечено во введении и доказано в разделе 2 «Повторные испытания».

Поэтому естественно дать следующее:

Математическим ожиданием или средним значением дискретной случайной величины, заданной своим рядом распределения, называется число

,где (i) означает суммирование по всем возможным значениям случайной величины.

 

ЗАМЕЧАНИЕ 1. Для случайной величины Y = φ(Х), где φ(Х) -некоторая функция, будем иметь следующий ряд распределения

Y	y1	y2	… .
Р	p1	p2	…

где у_i = φ(x_i). Поэтому из определения следует

ЗАМЕЧАНИЕ 2. Для краткости мы часто будем обозначать

М[Х]=m=m_x.

ПРИМЕР 1. Пусть ряд распределения случайной величины имеет вид

Х	1	3	7
Р	0.2	0.3	0.5

Тогда М[Х]=1^.0.2+3^.0.3+7^.0.5=4.6;

М[Х+1]= 2^.0.2+4^.0.3+8^.0.5=5.6;

М[2Х]= 2^.0.2+6^.0.3+14^.0.5= 9.2;

М[X²]=1^.0.2+9^.0.3+49^.0.5=27.4 и т.д.

ПРИМЕР 2. Рассмотрим распределение Пуассона

Х	0	1	2	…
Р	Р0	Р1	P2	…

, k=0,1,…

тогда

Рассмотрим свойства математического ожидания

1. М[C] = С, если С - неслучайная величина.

2. М[С^.Х] = C^.M[Х], если С-неслучайная величина.

1. 3.      М[Х+Y]=М[Х]+М[Y] (без доказательства).

2. 4.      М[Х^.Y]=М[Х]^.М[Y], если случайные величины Х и Y независимы.