Министерство образования и науки рф

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Московский государственный университет технологий и управления имени К.Г. Разумовского»

Филиал ФГБОУ ВПО «МГУТУ имени К.Г. Разумовского» в г. Мелеузе (Республика Башкортостан)

Высшая математика

Учебное пособие

для бакалавриата заочной формы обучения по квалификациям

220700.62 по направлению Автоматизация тех. процессов и производств

151000.62 по направлению Технологические машины и оборудование

140700.62 по направлению Ядерная энергетика и теплофизика

2012

Учебное пособие предназначено для студентов технологических и механических специальностей заочного отделения МГУТУ. При полном соответствии программе курса акцент сделан на сообщении студентам сведений, необходимых для практического применения математического аппарата в профессиональной деятельности. Предполагается, что доказательства некоторых теорем, и выводы части расчетных соотношений могут быть, при необходимости, разобраны по рекомендуемой литературе. Приведены необходимые графические иллюстрации и примеры решения типовых задач.

1. Двойной и тройной интегралы.

Д

Рис. 7.1

войной интеграл.Пусть функцияf(x, y)определена в замкнутой ограниченной областиDв плоскостихОу. Разобьем областьDнаnэлементарных областей, имеющих площадиS₁, S₂,…,S_n и диаметрыd₁, d₂,…,d_n. (Диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точкуp_i(_i, _i)и умножим значение функции в точкеp_iна площадь этой области. Интегральной суммой для функцииf(x, y) по областиD

называется сумма вида (7.1).

При f(x, y)  0каждое слагаемое можно рассматривать как объем малого цилиндра с основаниемS_iи высотойf (_i, _i), а сумму – как объем некоторого “ступенчатого” тела (геометрическая интерпретация). Способы разбиения областиDна элементарные могут быть различны, однако, если максимальный диаметр (диаметр наибольшей элементарной области) стремится к нулю (при этомn  ), то справедлива следующая теорема:

Если функция f(x, y) непрерывна в замкнутой области D, то предел интегральной суммы (7.1) при max d_i  0 существует и не зависит ни от способа разбиения области D на элементарные, ни от выбора точек внутри элементарных областей(теорема существования двойного интеграла). Этот предел называется двойным интегралом от функцииf(x, y) по областиD и

обозначается так: (7.2).

Область Dназывается областью интегрирования. Еслиf(x, y)  0в областиD, то двойной интеграл численно равен объему цилиндрического тела, ограниченного сверху поверхностьюz = f(x, y), сбоку цилиндрической поверхностью с образующими, параллельными осиОz(направляющая- граница областиD), и снизу областьюDплоскостихОу.

Основные свойства двойного интеграла определяются теоремами:

1. Двойной интеграл от суммы функций (х,у) и f(x, y) по области D равен сумме двойных интегралов по области D от каждой из функций, т.е.

(7.3)

2. Постоянный множитель можно вынести за знак двойного интеграла, т.е. если C = const, то (7.4).

3. Если областьD разбита на две области D₁ и D₂ без общих внутренних

точек, то (7.5).

В

Рис.7.2

ычисление двойного интеграла.Пусть областьDтакова, что всякая прямая, проходящая через внутреннюю точку области параллельно одной из осей координат пересекает границу области не более чем в двух точках (рис.7.2.). Если при этом областьDограничена линиямиу = ₁(х), у = ₂(х), х =а, х = b,причем₁(х)  ₂(х),а < b, а функции₁(х)и₂(х)непрерывны на отрезке[a, b], то область называютправильной в направлении осиОу. Аналогично определяется область правильная в направлении осиОх. Область, правильную в направлении обеих осей, называют простоправильной.

Для вычисления двойного интеграла по правильной области используется разновидность определённого интеграла по плоской области Dназываемаядвукратным интегралом и определяемая выражением:

(7.6)

В этом выражении сначала вычисляется интеграл по dy(«внутренний» интеграл, стоящий в скобках),при этомх считаетсяпостоянной. В результате получится непрерывная (доказательство не приводим) функция отх: 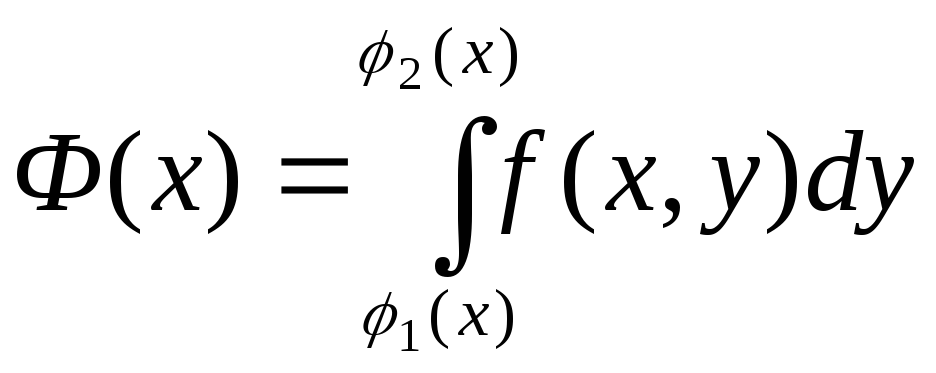. Эта функция интегрируется похв пределах отадоb: .

Пример: вычислить (ОбластьDпредставляет собой треугольник: а = 0;b= 1;₁(x) = 0 и₂(x) = х²). Вычислим

и затем .

Основные свойства двукратного интеграла:

1. Если правильную в направлении оси Оу(Ох) область D разбить на две области D₁ и D₂ прямой, параллельной оси Оу(Ох) то двукратный интеграл I_D по области D будет равен сумме таких же интегралов по областям D₁ и D₂, т.е. I_D = I_D1 + I_D2.

Следствие: двукратный интеграл по области D равен сумме двукратных интегралов по частичным областям, т.е. I_D = I _D1 + I _D2 + … +I _Dn (области D_i выбором границ можно сделать правильными в направлении оси Оу(Ох)).

2. (Оценка двукратного интеграла). Если m и М наименьшее и наибольшее значения функции f(x, y) в области D и S – площадь области D, то справедливо неравенство .

3. (Теорема о среднем) Двукратный интеграл от непрерывной функции f(x, y) по области D с площадью S равен произведению полощади S на значение функции в некоторой точке Р области D т.е. .

Свойства двукратного интеграла позволяют доказать теорему, открывающую путь к вычислению двойного интеграла:Двойной интеграл от непрерывной функцииf(x, y)по областиDравен двукратному интегралу от этой функции по областиD т.е. (7.7)

(Полагаем область Dправильная по осиОуи ограничена линиямиу = ₁(х), у = ₂(х), х =а, х = b).

Пример: Вычислить , если областьDограничена линиями у = 1 – х², у = 2х, х = – 2, х = 0. Построим областьD(рис.7.3). Очевидно, она правильная в направлении оси Оу и искомый интеграл равен двукратному интегралу

Отметим, что если областьDправильная в направлении осиОхи ограничена линиямих = ₁(у), х = ₂(у), у = с, у = dпричем₁(у)  ₂(у), то

(7.8).

Таким образом, двойной интеграл может быть вычислен по формулам (7.7) или (7.8). Пример: Изменить порядок интегрирования в интеграле. Область интегрирования ограничена прямой у = х и параболой(рис.7.4) и, очевидно, правильная, т.е. интеграл можно вычислить и по формуле (7.8)

полагая у²=₁(у), у =₂(у), с = 0,d= 1

откуда .

В случае, когда область Dне является правильной ни по одной из осей, двойной интеграл по этой области представить в виде двукратного нельзя. Однако, если областьDразбить на частичные, правильные в направлении той или иной оси, то двойной интеграл по областиDможно представить в виде суммы двойных интегралов по этим областям, а каждое слагаемое – в виде двукратного интеграла по соответствующей частичной области.

Вычисления с помощью двойного интеграла.

1. Объем.Напомним, что объемVтела, ограниченного сверху поверхностьюz = f(x, y)( f(x, y)  0), снизу – плоскостьюz = 0, а сбоку – цилиндрической поверхностью, направляющей для которой служит граница областиD, а образующая параллельна осиOz, определится соотношением

(7.9).

1.1. Если тело ограничено сверху поверхностью z = f₁(x, y)  0, снизу – поверхностьюz = f₂(x, y)  0, причем проекцией обеих поверхностей на плоскостьхОуявляется областьD, то объемVэтого тела равен разности объемов двух цилиндрических тел: оба имеют нижним основанием областьD, а верхним – поверхностиz = f₁(x, y)  0для первого иz = f₂(x, y)  0для второго,

(7.10)

Формула (7.10) верна и тогда, когда f₁(x, y)иf₂(x, y)– любые непрерывные функции, удовлетворяющие неравенствуf₁(x, y)  f₂(x, y).

1.2. Если в области Dфункцияf(x, y)меняет знак, то следует разбить область на две части:D₁, гдеf(x, y)  0иD₂, гдеf(x, y)  0. Если областиD₁иD₂таковы, что двойные интегралы по ним существуют, то первый будет равен объему тела, лежащего выше плоскостихОу, а второй – объему тела, лежащего ниже плоскостихОу.

2. Площадь плоской области. Площадь областиDв плоскостихОучисленно равна объему рассмотренного цилиндра, ограниченного сверху в нашем случае поверхностьюz = f(x, y) = 1, т.е. или, если областьDправильная(7.11).

3. Площадь поверхности, заданной уравнениемz = f(x, y)и ограниченной некоторой замкнутой линиейС. Проекцию этой линии на плоскостьхОуобозначим черезL, а область, ограниченную линиейL,обозначим черезD. Если функцияf(x, y)непрерывна и имеет непрерывные частные производные в этой замкнутой области, то искомая площадь поверхности определится выражением(7.12).

С помощью двойного интеграла можно решить и целый ряд “физических” задач: вычисление массы плоских пластин с известной поверхностной плотностью = f(x, y), момента инерции плоской фигуры и т.д.

Тройной интеграл. Пусть в декартовых трехмерных координатах задана «объемная» областьV, ограниченная замкнутой поверхностьюSи пусть в каждой точке этой области, включая границу, определена непрерывная функцияf(x, y, z). Разобьем областьVпроизвольным образом на малые области (объемы)V_i, выберем в каждой произвольную точкуР_i(x_i, y_i, z_i)и составиминтегральную сумму вида . Устремляя максимальный диаметрmaxd_i(и, соответственно, объемV_i) к нулю(maxd_i  0)перейдем к пределу интегральной суммы. При условиях, перечисленных выше, этот предел существует и называется тройным интегралом:

(7.13).

где dxdydz = dVэлемент объема в декартовых координатах. Еслиf(x, y, z)  0описывает плотность распределения вещества в объемеV, то (7.13) даст массу этого вещества.

Если: 1. Всякая прямая, параллельная оси Оzи проходящая через внутреннюю точку областиV, пересекает поверхностьSв двух точках;

2. Область Vпроектируется на плоскостьхОув правильную двумерную областьD; 3. всякая часть областиV, отсеченная плоскостью, параллельной одной из координатных обладает свойствами 1. и 2. – областьVназываютправильной.

Введем понятие трехкратного интеграла I_vпо областиVот функцииf(x, y, z)определенной и непрерывной в этой области. Пустьz = ₁(x,y)иz = ₂(x,y)уравнения поверхностей, ограничивающиxобластьVснизу и сверху (вместе они описывают замкнутую поверхностьS), а областьD– проекцияVна плоскостьxОу– ограничена линиямиу = ₁(х), у = ₂(х), х = а, x = b.

Трехкратный интегралI_vопределяется выражением:

(7.14)

При интегрировании по zпеременныехиусчитаем постоянными. После интегрирования поzи подстановки пределов получаем двукратный интеграл, рассмотренный в предыдущем разделе. Трехкратный интеграл обладает свойствами, аналогичными свойствам двукратного: 1.Если область V разбить на две областии V₁ и V₂ плоскостью, параллельной одной из координатных, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V₁ и V₂. (При любом разбиении областиVна конечное числоV₁, V₂,…,V_nплоскостями, параллельными координатным, справедливо равенство:I_V = I_V1 + I _V2 + … +I_Vn). 2.Если m и М – наименьшее и наибольшее значения функции f(x, y, z) в области V, то справедливо неравенство mV  I_v  MV, где V – объем области, I_v – трехкратный интеграл от f(x, y, z) по области V.

3. (теорема о среднем) Трехкратный интеграл I_v от непрерывной функции f(x, y, z) по области V равен произведению ее объема V на значение

функции в некоторой точке Р области V:

Приведенные свойства трехкратного интеграла позволяют доказать теорему о вычислении тройного интеграла:

Тройной интеграл от функции f(x, y, z) по правильной области V равен трехкратному интегралу по этой же области:

(7.15)

(Как и в случае двукратного интеграла, можно изменить порядок интегрирования, если это позволяет сделать форма области V. Можно с этой целью разбить областьVна части).

Если подинтегральная функция f(x, y, z) = 1, то тройной интеграл по областиVдает значение ее объема (7.15`).

Пример: , если областьVопределяется неравенствами: 0х½, ху2х, 0z(т.е. а = 0,b= ½,₁(x) =x,₂(x) = 2x,₁(x,y) = 0,₂(x,y) =, областьVпредставляет собой часть сферы единичного радиуса с центром в начале координат, ограниченную снизу плоскостью хОу(z= 0), а «с боков» плоскостями у = х и у = 2х).

Нередко вычисление тройных интегралов значительно упрощается при переходе к цилиндрическимилисферическимпространственным координатам.

В цилиндрических координатахположение точкиРопределяется тремя числами, , z,гдеи– полярные координаты проекции точкиРна плоскостьхОу, аz– аппликата точкиР. Пространственную областьVразбивают на элементарные координатными поверхностями = _i,  = _j, z = z_k.Элементарный объемdVпримет вид:dV = dddz, а тройной интеграл: , пределы интегрирования в соответствующем трехкратном интеграле определятся формой областиV. Зная формулы связи:

х = cos, y = sin, z = zнесложно перейти от декартовых координат к цилиндрическим: .

Пример: , если областьVограничена цилиндром х²+ у²= 2х и плоскостями у = 0,z= 0,z=a. Перейдем к цилиндрическим координатам. Уравнение цилиндра примет вид²cos²+²sin²= 2cos=>²(cos²+sin²) = 2cos=>= 2cos. ОбластьVопределяется неравенствами: 02cos, 0/2, 0zа и

В сферических координатахположение точкиРопределяется числами,, , где– расстояние точки от начала координат,– угол междуи осьюОzи– угол между проекциейна плоскостьхОуи осьюОх(отсчитывается, как обычно, от осиОхпротив часовой стрелки). Декартовы координаты связаны со сферическими так:х = sincos, у = sinsin, z = cos (0    , 0    2, 0    ). Элемент объема в сферических координатахdV = ²sinddd. В итоге можем перейти от тройного интеграла в декартовых координатах к тройному интегралу в сферических координатах.

Пример: , если областьV– верхняя половина шараx²+y²+z²r². Перейдя к сферическим координатам получим: 0r, 02, 0/2,x²+y²=²sin²cos²+²sin²sin²=²sin²и