Спектр атома водорода по Бору

Постулаты Бора позволили рассчитать спектр атома водорода и водородоподобных систем. Водородоподобными называют системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He⁺ , Li²⁺), где Z – порядковый номер атома в периодической системе электронов.

Решая совместно уравнения для момента импульса электрона

, (1)

и второго закона Ньютона для электрона массой и зарядоме, движущегося по окружности радиуса под действием кулоновской силы

(2)

получим выражение для радиуса электрона наn-й орбите

; ;

n² (n = 1, 2, 3, …). (3)

Из формулы (1) видно, что радиусы орбит пропорциональны n² , т.е. квантуются. Для атома водорода (z = 1) радиус первой орбиты электрона называется первым боровским радиусом и равен:

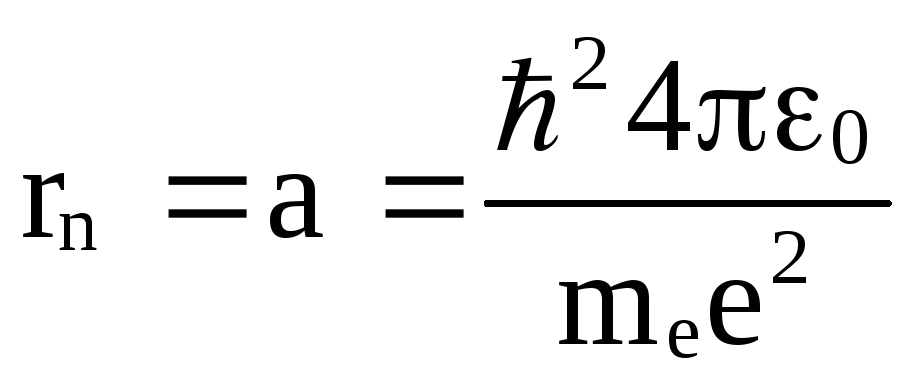= 0,53 10^-10 м

Полная энергия электрона Е складывается из его кинетической энергии (m_ev²/2) и потенциальной энергии в электростатическом поле ядра ().

Е = .

Из выражения (1): =. Тогда Е = +

Е = -.

Подставляя квантованные радиусы r_n из (3), получим:

(4)

Здесь знак минус означает, что электрон находится в атоме в связанном состоянии.

Из формулы (4) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от числа n. Это число называют главным квантовым числом. Энергетическое состояние с n = 1 называется основным (нормальным) состоянием; с n > 1 – возбужденными. Энергетический уровень при n = 1 называется основным, все остальные - возбужденными.

Атом водорода обладает наименьшей энергией при n = 1, Е = -13,55 эВ. При n →∞ (при удалении электрона из атома) =0. Энергия Е_n = - E₁, будет энергией ионизации атома.

Согласно 2-му постулату Бора при переходе атома из стационарного состояния с большей энергией Е_n в состояние с меньшей энергией Е_m испускается квант энергии hν равной Е_n-E_m

,

частота излучаемого кванта энергии будет равна

,

Здесь R = - постоянная Ридберга.

Подставляя в формулу m = 1, n = 2, 3, 4,… получим группу линий серии Лаймана, а при m = 2, n = 3, 4, 5, … - серию Бальмера и т.д. (рис. 173).

Таким образом теория Бора объяснила переход атома в данное состояние из возбужденных состояний, расположенных выше данного, сопровождающееся испусканием соответствующего кванта излучения.

Спектр поглощения атома водорода является линейчатым, но содержит только серию Лаймана. Свободные атомы водорода обычно находятся в основном состоянии (n = 1) с наименьшей энергией. При сообщении атомам извне определенной энергии могут наблюдаться лишь переходы атомов из основного состояния (n = 1) в возбужденные (m = 2, 3, 4, …), что приводит к появлению в спектре поглощения только линий серии Лаймана.

Рис. 173

Элементы современной (квантовой) физики атомов и молекул Атом водорода в квантовой механике

Решение задачи об энергетических уровнях электрона в атоме водорода сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия U(r) взаимодействия электрона с ядром, обладающим зарядом Z·е, имеет выражение

U(r) =,

где r – расстояние между электронами и ядром.

С уменьшением r потенциальная энергия U(r) неограниченно убывает (увеличивается по модулю) при приближении электрона к ядру. Графически функция U(r) изображена на рис. 174 непрерывной гиперболической кривой.

Ядро и электроны имеют разные знаки зарядов. Для удаления электрона от ядра требуется работа внешних сил, и тем большая, чем ближе электроны к ядру. Поэтому потенциальная энергия электрона уменьшается (возрастая по абсолютной величине) с приближением электрона к ядру. С другой стороны, за уровень отсчета потенциальной энергии принята потенциальная энергия электрона на бесконечности

U(r) =; U(∞) = 0.

Таким образом, с уменьшением r потенциальная энергия U(r) уменьшается, возрастая по абсолютной величине. Примером обратного свойства является потенциальная энергия тела, поднятого над поверхностью Земли.