Пример 2.2
Используя исходные данные предыдущего примера (табл. 2.1) провести расчет параметров логарифмического тренда и сделать прогноз на 15, 16 и 17 месяцы. Построить графики ряда динамики и тренда.
Для нелинейных функций, например логарифмической, степенной, экспоненциальной и других процессу построения системы нормальных уравнений предшествует этап линеаризации кривой, предусматривающий переход от нелинейных связей к линейной зависимости изменения признака. С этой целью осуществляется замена переменных.
Составим
систему нормальных уравнений для
логарифмической прогнозирующей функции
=a+bln
t.
Для этого необходимо выполнить замену переменных
Линеаризованное уравнение — yt = a + b t1 ,
где t1= ln t;
Система нормальных уравнений:
yt = an + b t1
yt t1 = a t1 + b t12
Сомножитель nв первом уравнении системы характеризует объем выборочной совокупности (n = 14).
Определим все суммы, включенные в систему нормальных уравнений. Результаты вычислений удобно записать в специальную таблицу (табл. 2.2).
Таблица 2.2
-
Месяцы, t
объем продаж онкологических препаратов (тыс. руб.), yt
ln t
yt lnt
(lnt)2
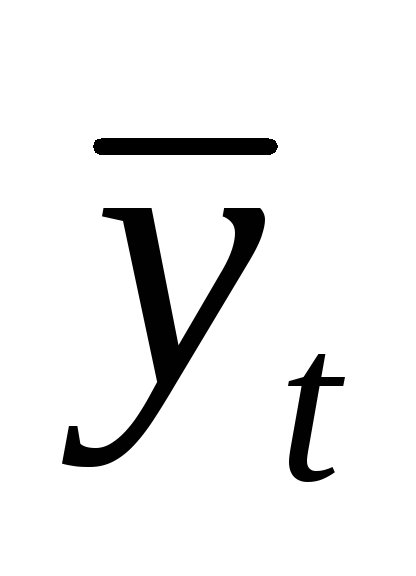(прогноз.)1
145
0,000
0,000
0,000
110,195
2
314
0,693
217,648
0,480
278,167
3
430
1,099
472,403
1,207
376,425
4
525
1,386
727,805
1,922
446,140
5
347
1,609
558,475
2,590
500,215
6
295
1,792
528,569
3,210
544,397
7
426
1,946
828,958
3,787
581,753
8
603
2,079
1253,903
4,324
614,112
9
548
2,197
1204,079
4,828
642,655
10
598
2,303
1376,946
5,302
668,187
11
665
2,398
1594,600
5,750
691,284
12
808
2,485
2007,805
6,175
712,370
13
898
2,565
2303,325
6,579
731,767
14
825
2,639
2177,222
6,965
749,726
Всего: 105
7427
25,191
15251,738
53,118
7647,394
Таким образом:
t1 = ln t = 25,191; t12 = 53,118; yt = 7427; yt t1 = 15251,738.
Подставим полученные результаты в систему
7427 =14a +25,191b;
15251,738= 25,191a + 53,118b.
Решив систему, найдем константы прогнозирующей функции:
a =110,195;b = 242,333.
Следовательно, уравнение прогноза имеет вид:
= 110,195+
242,333lnt
Зная параметры
уравнения тренда, можно определить
расчетные значения переменной
для всех месяцев предпрогнозного
периода. Так расчетная величина (t
= 1) составляет:
yt=1 = 110,195+ 242,333ln1= 110,195 тыс.руб.
После того как получили логарифмический тренд, можно прогнозировать развитие процесса в будущем. Для этого надо просто подставить в формулу значения t= 15, 16, 17.
Расчеты выполним по формулам:
yt=15 = 110,195+ 242,333ln15 = 766,44 тыс.руб.
yt=16 = 110,195+ 242,333ln16 = 782,08 тыс.руб.
yt=17 = 110,195+ 242,333ln17 = 796,78 тыс.руб.