8. Вычисление объемов тел вращения

Рассмотрим тело, образованное вращением вокруг оси криволинейной трапеции(рис. 8.8.), ограниченной кривой, осьюи прямымиВ этом случае любое сечение полученного тела плоскостью, перпендикулярной оси, есть круг радиуса, площадь которого равна.

Составим интегральную сумму. Разобьем отрезокпроизвольно начастей. Возьмем частичный отрезок, выберем на нем произвольную точку. В точкахивосставим перпендикуляры и построим элементарный прямоугольник высотоюс основанием, (рис. 8.9.). В результате вращения этого прямоугольника вокруг осиполучится элементарное цилиндрическое тело, радиус которого, а высота. Объем такого цилиндрического тела равен, а сумма всехэлементарных цилиндрических тел дает интегральную сумму

Последовательность интегральных суммдля непрерывной на отрезкефункции прииимеет предел. Его и называютобъемом тела вращения вокруг координатной оси , то есть

, короче (8.9)

Аналогично, объем тела вращения вокруг оси следует вычислить по формуле

или(8.10)

Если вокруг оси вращается фигура, ограниченная двумя кривымии, причем<на отрезке, то

(8.11)

Аналогично для фигуры, вращающейся вокруг оси

(8.12)

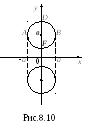
Пример 8.12. Найти объем тора, образованного вращением круга вокруг оси. Предполагается, что.

Решение. Круг радиусас центром в точке с координатамибудем рассматривать как фигуру, ограниченную дугами двух полуокружностей:

верхней(дугаADB, рис. 8.10)

и нижней (дугаAFB).

По формуле (8.11) получим

Употреблена подстановка Новые пределы интегрирования такие:припри.

8. Приближенное вычисление определенных интегралов

Мы уже знаем, что первообразные некоторых функций не могут быть выражены в конечном виде через элементарные функции. Вычисление определенных интегралов от таких функций возможно с помощью приближенных методов, которые целесообразно применять и в случаях интегрируемости функции в конечном виде, когда отыскание первообразной требует сложных выкладок.

Формулы приближенного вычисления определенного интеграла связаны с геометрическим решением задачи о нахождении площади криволинейной трапеции.

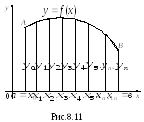Пусть требуется найти приближенное значение определенного интеграла. Рассмотрим площадь криволинейной трапеции(рис. 8.11) как геометрическое представление заданного интеграла и будем искать способы приближенного вычисления этой площади.

Разделим отрезок и наравных частей точками. Расстояние между каждой парой соседних точек

Из точек деления отрезка восставим перпендикуляры к осидо пересечения с графиком функции. Это будут ординаты соответствующих точек деления:

Площадь криволинейной трапеции можно рассматривать как сумму площадейчастичных криволинейных трапеций, на которые разделена фигура:.

1. Формулы прямоугольников

Заменим площадь каждой частичной криволинейной трапеции площадью прямоугольника с основанием и высотой, равной его левой ординате. Тогда приближенное значение площади фигурывыразится суммой

Иначе говоря, получим следующую формулу приближенного интегрирования

(8.11)

Если же в качестве высот прямоугольников возьмем их правые ординаты, то площадь фигуры выразится суммой

что дает аналогичную формулу

(8.12)

Формулы (8.11) и (8.12) называются формулами правых и левых прямоугольников. Иногда используется формула средних прямоугольников:

.