Лекция 8. Определенный интеграл

Определенный интеграл связан с непосредственным приложением интегрального исчисления к решению прикладных задач. Введем понятие определенного интеграла и познакомимся с его свойствами и методами вычисления.

8.1. Задача о площади криволинейной трапеции

Пусть дана функция, непрерывная на отрезкеи неотрицательная на этом отрезке. Фигураназывается криволинейной трапецией. Разобьем отрезокнапроизвольных частей точками x₀, x₁, x₂, x₃,…,x_n. Частичные отрезки обозначим как приращения аргумента, ,Внутри каждого частичного отрезкавыберем точкуи вычислим значение функциив точках, то есть. Каждое произведениеесть площадь прямоугольника, имеющая основаниеи высоту. Суммируя все, получиминтегральную сумму:

. (8.1)

Предел интегральной суммы (8.1) при всегда существует и не зависит ни от способа разбиения отрезкана частичные отрезки при указанном выше условии, ни от выбора точек. Этот предел называется определенным интегралом функциина отрезкеи обозначается так

(8.2)

где пределы (границы) интегрирования. Названия остальных элементов обозначения такие же, как в неопределенном интеграле.

Определенный интеграл (8.2) численно равен площади криволинейной трапеции .

Аналогично составляются интегральные суммы и при решении других прикладных задач, о чем мы скажем ниже.

8.2. Свойства определенного интеграла

1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю, то есть .

2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный, то есть.

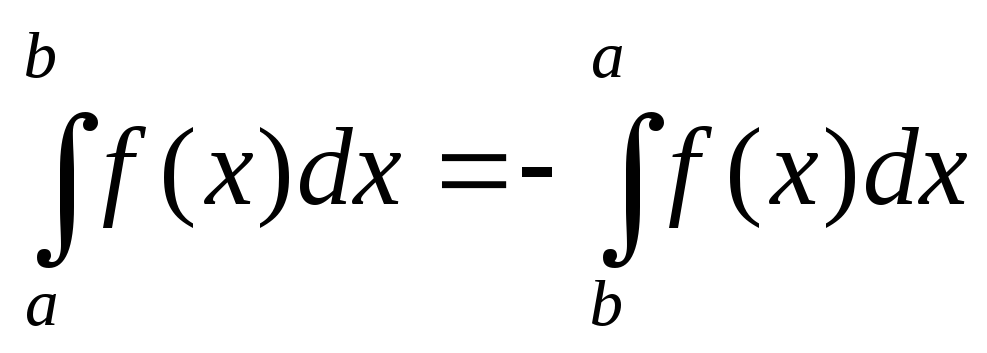3. Постоянный множитель можно выносить за знак определенного интеграла, то есть 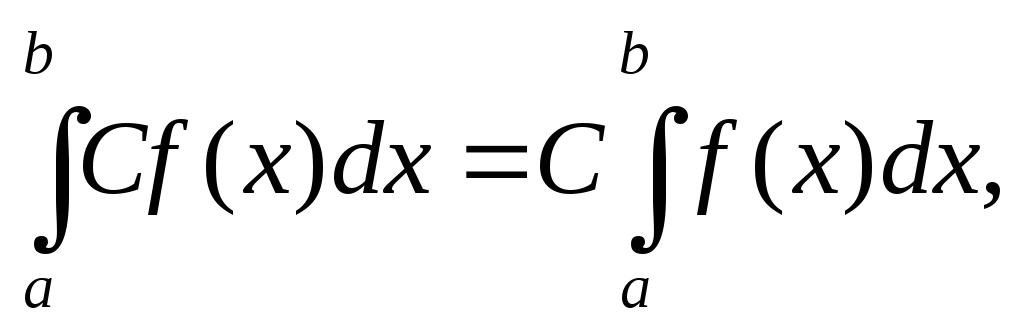где

4. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от этих функций:

.

5. Если отрезок интегрирования разбит на части, то определенный интеграл по всему отрезку равен сумме определенных интегралов по его частям, например, еслиa<c<b, то .

6. Если на отрезке интегрирования , гдеa< b функция и обе эти функции непрерывны, то.

7. Если т – наименьшее, М - наибольшее значения непрерывной на отрезке функции, то.

8. Теорема о среднем. Определенный интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой внутренней точке с этого отрезка, то есть

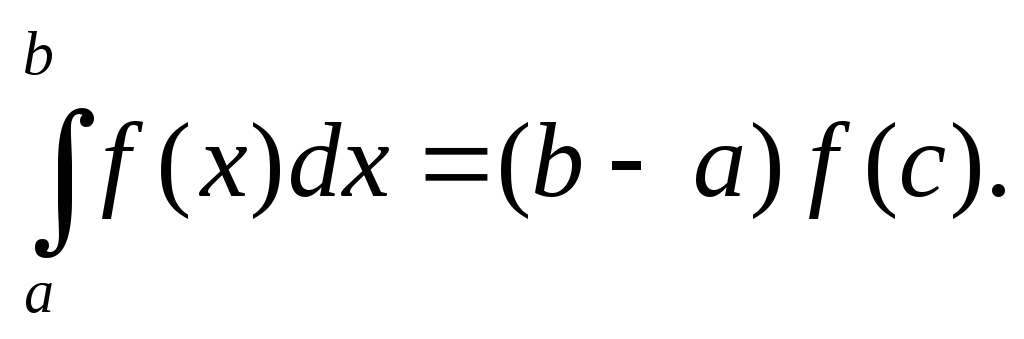
Отсюда получаем интегральную среднюю как среднее значение функции на отрезке:

(8.3)

9. Определенный интеграл не зависит от обозначения переменной интегрирования. Он зависит от подынтегральной функции и границ интегрирования.

8.3. Вычисление определенного интеграла. Формула Ньютона-Лейбница

Для вычисления определенных интегралов применяется простая и удобная формула Ньютона-Лейбница, названная так в честь изобретателей дифференциального и интегрального исчислений.

Формула имеет вид:

(8.4)

Она устанавливает связь между определенным и неопределенным интегралами. Благодаря этой связи, отпала необходимость нахождения всякий раз пределов интегральных сумм, попытки которых предпринимались не раз со времен Архимеда. Формула Ньютона-Лейбница способствовала решительному и быстрому внедрению методов интегрирования в практику. Благодаря ей математика получила общий метод для решения многих частных задач и смогла значительно расширить круг приложений.

Пример 8.1. Вычислить

Пример 8.2.

Вычислить