2.7. Основы алгебры логики.

Алгебра логики – наука, которая занимается логическими функциями, описанием работы и синтезом с их помощью схем различных устройств ЦВМ. Алгебра логики имеет дело с высказываниями. Высказывания могут быть истинными или ложными. Если высказывание истинно, то значение истинности равно 1, если ложно -0. Высказывания могут быть простые и сложные, которые образуются из простых с помощью элементарных логических операций. Простые высказывания обычно называются также логическими переменными, сложные высказывания - логическими функциями.

Основные элементарные логические операции:

1. Логическое отрицание. Обозначается чертой над логической переменной. Например 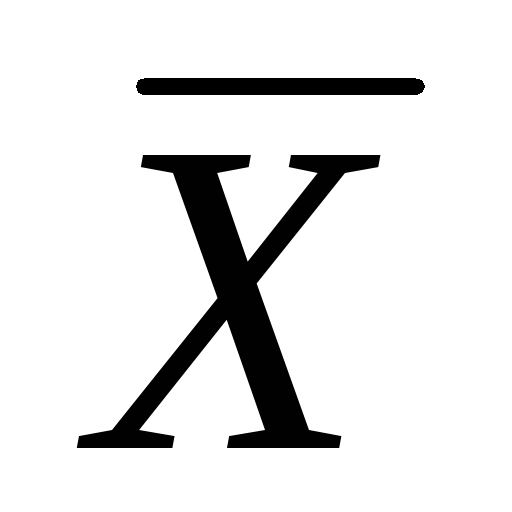читается “не Х”.

Каждая логическая операция характеризуется таблицей истинности, которая показывает значение функции при всех значениях переменных. В данном случае таблица истинности содержит одну переменную, т.е.

Х

0 1

1 0

Изображение логического элемента “НЕ” на структурной схеме показано на рис. 2.14а.

Рис. 2.14. Изображение основных логических элементов.

а) элемент «НЕ»; б) элемент «ИЛИ»; в) элемент «И»

2. Логическое сложение (дизъюнкция). Обозначается значком V. Например Х₁VХ₂читается как “Х₁или Х₂”.Результаты логического сложения истинен (1) коли хотя бы одна из переменных (Х₁илиX₂) истинна (1)

Таблица истинности

Х1	Х2	Х1VХ2
0 0 1 1	0 1 0 1	0 1 1 1

Изображение логического элемента “ИЛИ” на структурной схеме показано на рис.2.14 б.

3) Логическое умножение (конъюнкция). Обозначается значком ^. Например Х1^Х2 читается “Х₁и Х₂”. Результат логического умножения истинен (1), только тогда, когда обе переменных истинны (1)

Таблица истинности

Х1	Х2	Х1^Х2
0 0 1 1	0 1 0 1	0 0 0 1

Изображение логического элемента “И” на структурной схеме показано на рис.2.14в:

Основные законы алгебры логики:

1. Переместительный

2. Сочетательный

3. Распределительный

4. Отрицания

Справедливость любого закона может быть показана с помощью таблицы истинности.

Покажем справедливость последнего закона

Х1	Х2
0 0 1 1	0 1 0 1	0 0 0 1	1 1 1 0	1 1 0 0	1 0 1 0	1 1 1 0

Из таблицы видно, что при всех сочетаниях значений логических переменных Х₁и Х₂значения логических функцийисовпадают. Следовательно, эти логические функции тождественны, т.е. закон справедлив.

Основные формулы, используемые при упрощении логических функций

Синтез схемы одноразрядного двоичного сумматора с двумя входами (логического полусумматора).

Составим таблицу работы сумматора в соответствии с двоичной таблицей сложения

Х1	Х2	S	P
0 0 1 1	0 1 0 1	0 1 1 0	0 0 0 1

Здесь Х₁и Х₂– входы (слагаемые),S– сумма,P– перенос в следующий (старший) разряд.

Запишем логические функции SиPиз условий их истинности:

Рис. 2.15. Структурная схема логического полусумматора

Структурная схема логического полусумматора показана на рис. 2.15. Упростим логическую функцию S

Обозначим , тогда

Структурная схема логического полусумматора после упрощения (минимизации) логической функции S, показана на рис.2.16. Эта схема в отличие от предыдущей (рис.2.15) содержит на 2 элемента меньше.

Рис. 2.16. Структурная схема логического полусумматора после

упрощения логической функции S.

На рис. 2.17 показано условное обозначение логического одноразрядного полусумматора.

Рис. 2.17. Условие изображение одноразрядного полусумматора

Схема логического многоразрядного сумматора состоит из ряда одноразрядных сумматоров, у которых, кроме, младшего, имеются 3 входа (2 слагаемых и 1 перенос из предыдущего сумматора). На рис. 2.18 показана схема 4-х разрядного сумматора. Работа сумматора иллюстрируются на примере сложения двоичных чисел Х₁=110 и Х₂=11. при этомS=1001.

Рис. 2.18. Условное изображение 4-х разрядного сумматора