
- •Федеральное агентство по образованию рф
- •Содержание
- •Глава 1. Основы теории информации 10
- •Глава 2. Основы аналоговых и цифровых вычислений 50
- •Предисловие
- •Введение Основные понятия
- •Вопросы для самоконтроля
- •Глава 1. Основы теории информации
- •Получение информации
- •Сигналы детерминированные и случайные.
- •1.3 Сигналы непрерывные и дискретные. Преобразование сигналов.
- •1.4 Модуляция и демодуляция сигналов.
- •1.5 Передача информации. Меры информации.
- •Вопросы для самопроверки
- •Тестовые задания
- •Глава 2. Основы аналоговых и цифровых вычислений
- •2.1. Принципы построения вычислительных машин
- •2.2.Арифметические основы цвм. Системы счисления
- •2.3.Двоичная система счисления.
- •2.4. Перевод чисел из одной системы счисления в другую.
- •Пример. Перевести двоичное число 1110101111,01101112 в шестнадцатеричную систему счисления
- •2.5. Формы представления числовой информации
- •2.6. Прямой, обратный и дополнительный коды и их использование при выполнении арифметических операций
- •Пример. Число: -1
- •Пример. Число –127
- •2.7. Основы алгебры логики.
- •Основные формулы, используемые при упрощении логических функций
- •Составим таблицу работы сумматора в соответствии с двоичной таблицей сложения
- •Вопросы для самоконтроля
- •Тестовые задания
- •Итоговые тестовые задания
- •Ответы на тесты по главам
- •Список рекомендуемой литературы
- •Основы информатики и вычислительной техники
Пример. Перевести двоичное число 1110101111,01101112 в шестнадцатеричную систему счисления
![]()
3 А F 6 Е 1110101111,011011102=3AF,6E16
Следует отметить, что помимо систем счисления в ЦВМ используются различные коды, например “2-10” код. Для представления десятичного числа в “2-10” коде каждую цифру числа представляют в виде тетрады.
Пример. Представить число 563,9110в “2-10” коде
5 6 3 9 1 10
0101 0110 0011 1001 0001 563,9110=0101 0110 0011,1001 00012-10
2.5. Формы представления числовой информации
Существует две формы представления чисел: естественная или с фиксированной запятой (точкой) и нормальная или с плавающей запятой.
Представление чисел с фиксированной
запятойхарактеризуется тем, что
положение запятой фиксируется перед
каким-либо разрядом, например, перед
старшим разрядом. В этом случае для
машинного изображения![]() числа Х должно выполняться условие
числа Х должно выполняться условие
![]() (2.11)
(2.11)
т.е. числа имеют вид правильных дробей.
В этом смысле число Х будет представлено
в виде
![]() ,
где К масштабный коэффициент, величина
которого удовлетворяет условию (2.11).
Так как числа бывают положительные и
отрицательные, то формат (разрядная
сетка) разбивается на знаковую часть и
поле числа (рис. 2.8а). В знаковую часть
записывается информация о знаке. Обычно
знак положительного числа «+» изображается
символом 0, а знак отрицательного числа
«-» изображается символом 1.
,
где К масштабный коэффициент, величина
которого удовлетворяет условию (2.11).
Так как числа бывают положительные и
отрицательные, то формат (разрядная
сетка) разбивается на знаковую часть и
поле числа (рис. 2.8а). В знаковую часть
записывается информация о знаке. Обычно
знак положительного числа «+» изображается
символом 0, а знак отрицательного числа
«-» изображается символом 1.
Диапазон представимых чисел составляет
от
![]() до
до![]() ,
гдеn- количество разрядов
без знаковой части
,
гдеn- количество разрядов
без знаковой части

|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Поле числа
б) Знаковая часть
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
в)
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
Рис. 2.8. Представление чисел в форме с фиксированной запятой.
Задача выбора масштабного коэффициента К усложняется в связи с необходимостью сохранять соответствие разрядов всех чисел, с которыми оперирует компьютер.
Пусть разрядная сетка ЦВМ содержит 12
двоичных разрядов (рис. 2.8а). Надо
определить масштабный коэффициент для
чисел
![]() и
и![]()
Для того, чтобы выполнить условие (2.11)
необходимо число, большее по абсолютному
значению, записать в виде
![]() .
Отсюда
.
Отсюда![]() (рис.2.8б), что соответствует величине
масштабного коэффициента
(рис.2.8б), что соответствует величине
масштабного коэффициента![]() .
Число Х2должно войти в разрядную
сетку с сохранением соответствия
разрядов, т.е.
.
Число Х2должно войти в разрядную
сетку с сохранением соответствия
разрядов, т.е.![]() .
Следовательно,
.
Следовательно,![]() или
или![]() (рис. 2.8 в).
(рис. 2.8 в).
Из данного примера видно, что представление
чисел в форме с фиксированной запятой
может привести к погрешности представления.
Так, для числа Х2абсолютная
погрешность представления оценивается
величиной части числа, не уместившейся
в разрядную сетку, т.е. величиной![]() .
В некоторых случаях очень малые числа
представляются в машине изображением,
называемым машинным нулем. Если в
результате какой-либо операции появится
число, по абсолютному значению большее
единицы, то возникает переполнение
разрядной сетки, что нарушает нормальное
функционирование ЦВМ.
.
В некоторых случаях очень малые числа
представляются в машине изображением,
называемым машинным нулем. Если в
результате какой-либо операции появится
число, по абсолютному значению большее
единицы, то возникает переполнение
разрядной сетки, что нарушает нормальное
функционирование ЦВМ.
Представления чисел в форме с плавающей запятойхарактеризуется тем, что число представляется в нормальной форме
![]() , (2.12)
, (2.12)
где m– мантисса числа х; р - порядок числа х.
Такое представление числа неоднозначно.
Например, десятичное число 485,00 можно
записать различными способами:
![]()
Для определенности обычно вводят некоторые ограничения. Наиболее распространено и удобно для распространения в ЭВМ ограничение вида
![]() , (2.13)
, (2.13)
где q– основание системы счисления. Из этого
следует, что мантисса должна быть
правильной дробью, первая цифра которой
отлична от нуля:![]() Мантиссу и порядокq–ичного числа принято записывать в
системе с основаниемq, а
само основание в десятичной системе.
Мантиссу и порядокq–ичного числа принято записывать в
системе с основаниемq, а
само основание в десятичной системе.
Форма представления чисел, для которой
справедливо условие (2.13) называется
нормализованной. Поскольку в этом случае
абсолютное значение мантиссы находится
в пределах
![]() гдеn– количество разрядов
изображения мантиссы без знака. Поскольку
положение разрядов числа в разрядной
сетке машины не постоянно, такую форму
представления чисел называют также
формой представления с плавающей
запятой. Формат машинного изображения
числа с плавающей запятой должен
содержать знаковые части и поля для
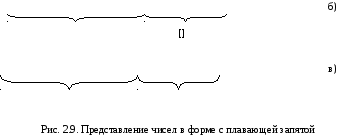
числа (мантиссы) и порядка (рис. 2.9а).
Кодирование знаков остается таким же,
как и при представлении чисел с
фиксированной запятой.
гдеn– количество разрядов
изображения мантиссы без знака. Поскольку
положение разрядов числа в разрядной
сетке машины не постоянно, такую форму
представления чисел называют также
формой представления с плавающей
запятой. Формат машинного изображения
числа с плавающей запятой должен
содержать знаковые части и поля для
числа (мантиссы) и порядка (рис. 2.9а).
Кодирование знаков остается таким же,
как и при представлении чисел с
фиксированной запятой.

|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Рассмотрим пример записи чисел в форме
с плавающей запятой. Пусть требуется
записать в разрядную сетку ЦВМ двоичные
числа
![]() .
Эти числа следует представить в
нормализованном виде, т.е. при выполнении
условия (2.13):
.
Эти числа следует представить в
нормализованном виде, т.е. при выполнении
условия (2.13):
![]()
Поскольку для изображения порядка выделено пять цифровых разрядов и один разряд для знака, машинные изображения порядков:
![]()
машинные изображения их мантисс соответственно:
![]()
Представление чисел Х1и Х2в разрядной сетке показано на рис. 2.9 б,в соответственно.
В современных ЦВМ используется оба способа представления чисел, каждый из которых имеет свои достоинства и недостатки. Представление чисел в форме с фиксированной запятой хотя и доставляет некоторые трудности при программировании, связанные с введением масштабов, позволяет упростить схемы АЛУ и повысить его быстродействие, так как арифметические операции над числами выполняются без предварительных действий (выравнивания порядков).
Пример. Сложить два двоичных положительных числа 0,0000011 и 0,0000111
|
|
0,0000011 |
|
+ |
|
|
|
0,0000111 |
|
|
0,0001010 |
(710)
1010Представление чисел с плавающей запятой, хотя и обеспечивает максимальную точность представления, но усложняет схемы АЛУ, так как при сложении (вычитании) требует подготовительной операции – выравнивания порядков.
Пример. Сложить два двоичных нормализованных
положительных числа
![]() и
и![]() .
Разность порядков слагаемых здесь равна
трем, поэтому перед сложением мантисса
первого числа сдвигается на три разряда
вправо
.
Разность порядков слагаемых здесь равна
трем, поэтому перед сложением мантисса
первого числа сдвигается на три разряда
вправо
![]()
![]()
![]()
Результат получился нормализованным. В противном случае его бы следовало нормализовать в соответствии с условием (2.13).
