Глава III. Теплопроводность

Если в двух соседних областях термодинамической системы имеют мес-то различные температуры, то вследствие различия теплового движения со-ставляющих её частиц , она стремится придти в состояние равновесия, при котором температуры выравниваются. Процесс переноса тепловой энергии из области с более высокой температурой в область с более низкой, обусловленный тепловым движением атомов или молекул, носит название теплопроводности. Хотя в деталях этот процесс в газах, жидкостях и в твердых телах различается, математическая запись процесса подчиняется закону Фурье: Плотность теплового потока, т.е. тепловая энергия, переносимая через единичную изотермическую площадку в единицу времени, пропорциональна градиенту температуры: , где ΔQ – количество теплоты; S - площадь площадки; - коэффициент теплопроводности;T - термодинамическая температура; Δ t – промежуток времени, в течение которого через площадку проходит количество теплоты равное ΔQ . Координата x совпадает с направлением нормали к площадке. Знак «-» означает, что теплота перемещается от облас-ти с большей температурой к области с меньшей температурой.

В общем случае уравнение закона Фурье может быть представлено в векторной форме:

J_Q = - χ grad T,

где J_Q - плотность теплового потока; grad – оператор градиента. Таким образом, различия в теплопроводности различных фаз по величине связаны с различием значений коэффициентов теплопроводности, а по существу‒ в раз-личиях механизмов передачи тепла.

При постановке задачи об определении переноса тепла в жидкостях и газах необходимо учитывать то обстоятельство, что теплопередающая среда находится в поле тяготения Земли. Поэтому на процесс теплопередачи может налагаться передача тепла посредством конвекционных потоков. Последнее явление отнюдь не является теплопроводностью.

Молекулярно-кинетическая теория теплопроводности в газах

В курсе физики уже приводились основы молекулярно-кинетической теории газов. Было показано, что газ состоит из хаотически движущихся молекул, кинетические энергии которых определяются температурой газа. Средняя длина свободного пробега молекулы в идеальном газе <λ> равна : , где n₀ - количество частиц в единице объема; d - эффектив-ный диаметр молекулы. Таким образом, если условно выделить некую плоскость, разделяющую области газа с температурой и, то в слоях толщинойс двух сторон этой плоскости будет происходить взаимный обмен кинетической энергией между молекулами из областии. Очевидно, чтобы исключить влияние конвекции в поле силы тяжести, следует предполагать, что область с более высокой температурой располо-жена над областью с более низкой. Если каким-либо гипотетическим спосо-бом исключить приток в промежуточную область молекул изи, то че-рез некоторый промежуток времени в ней установится температураТ, про-межуточная между и.

Для определения коэффициентов переноса в средах в общем случае сле-дует решать кинетическое уравнение Больцмана, что является предметом ис-следования физической кинетики. Применение молекулярно-кинетических представлений позволило получить формулу для коэффициента теплопро-водности в уравнении Фурье для идеального газа в виде: , гдеρ – плотность газа; c_V –удельная теплоемкость при постоянном объеме; (c_V = iR/(2M) ); i - число степеней свободы молекулы; R - универсальная газовая постоянная; <υ> - среднеарифметическая скорость молекулы, ;M – молярная масса. После соответствующих подстановок для коэффициента теплопроводности идеального газа получим: . Следует отметить связь коэффициентов теплопроводности (χ) и вязкости (η) для идеального газа: .

Теплопроводность кристаллов. Неэлектропроводные вещества

Носителями и передатчиками тепла в твердых телах, в принципе, могут быть акустические колебания ( фононы ) и свободные электроны, если они имеются. Поэтому механизм теплопередачи в кристаллах зависит от того, являются ли они проводниками или изоляторами. Поскольку в кристаллах непроводящих веществ свободные электроны отсутствуют, теплопередача в них осуществляется исключительно по фононному механизму, т.е. за счет коллективных колебаний частиц в узлах кристаллической решетки.

Как было указано в предыдущей главе, фононы представляют собой квазичастицы, хаотически движущиеся в кристаллической решетке твердого тела. Фононы движутся со скоростью звука и взаимодействуют с неоднородностями структуры решетки. Поэтому фононы, содержащиеся в кристалле, можно интерпретировать, как идеальный газ, и описывать его поведение в соответствии с закономерностями идеального газа. В частности, используем для определения коэффициента теплопроводности формулу, полученную выше для идеального газа, с соответствующими заменами:

,

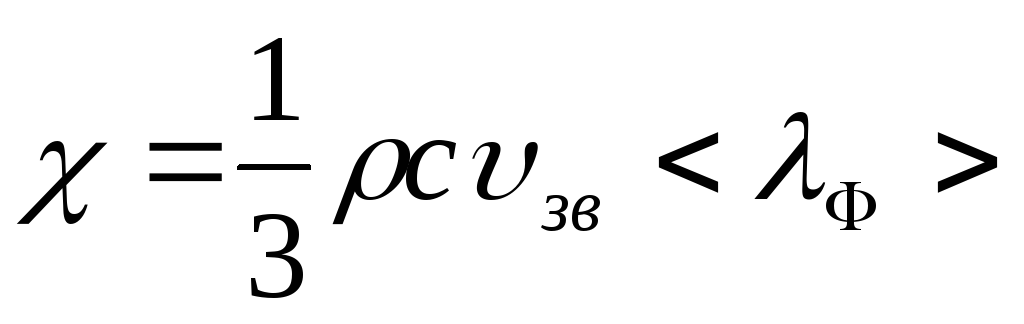где ρ и c – плотность и удельная теплоемкость кристаллического вещества; - скорость звука в кристалле;- средняя длина свободного пробега фононов.

Полученная формула дает возможность анализировать зависимость χ от температуры. При температуре, превышающей дебаевскую, χ ~ ~ 1/T. Следует, однако, отметить, что при высокой температуре наблюдается сильное рассеяние фононов не только на неоднородностях структуры, но и в результате фонон-фононного рассеяния. Поэтому теоретическое определе-ние является сложной задачей. При температуре меньшей, чем дебаев-ская, но не очень низкой, такжеχ ~ ~ 1/T, а при Т→0 χ ~ Т³ вследствие того, что c ~ Т³.

Теплопроводность кристаллов. Металлические кристаллы

В металлах механизм передачи тепла зависит от температуры. При высо-кой температуре основной вклад в теплопроводность дает электронный меха-низм, связанный с наличием электронов проводимости. Из электронной тео-рии металлов известно, что электроны проводимости в металлах ведут себя аналогично идеальному одноатомному газу, который может передавать энергию. Кроме того, из-за высокой подвижности электронов проводимости в них легче возбудить движение. Электронный газ передает энергию движе-ния кристаллической решетке в результате рассеяния на фононах. Вслед-ствие этого, коэффициенты переноса можно определять по молекулярно-ки-нетической теории идеального газа. Коэффициент теплопроводности в ме-таллах при средних и высоких температурах определяется по формуле: , гдеn_эл – плотность электронного газа; c_элV - удельная теплоемкость электронного газа при постоянном объеме; < υ_эл > - среднеарифметическая скорость электронов; < λ_эл > - средняя длина свобод-ного пробега электронов проводимости в металле. После подстановки в полученную формулу входящих в неё величин, получаем:

χ = n_эл < λ_эл > (kπ)² T/ (3p_F),

где k - постоянная Больцмана; T - температура электронного газа; p_F - импульс электрона, находящегося на уровне Ферми ( от температуры не зави-сит ). Анализ величин, входящих в эту формулу, показывает, что при средних температурах величина не зависит от температуры. При очень высоких температурах для некоторых металлов оказывается, т.е. снижается.

При очень низких температурах энергия, переносимая электронами про-водимости, становится слишком малой для возбуждения тепловых колебаний атомов в узлах решетки. Поэтому электронный механизм теплопередачи ста-новится не эффективным и превалирует фононный механизм, описанный вы-ше для объяснения механизма теплопроводности в непроводящих вещест-вах. Полученный там вывод о том, что при 0 коэффициент теплопро-водностисраведлив также и для металлических кристаллов.