Свойства жидкостей

В отношении молекулярного строения жидкости занимают промежуточное положение между твердыми телами и газами. Вследствие специфики взаимодействия между молекулами в жидкой фазе последняя обладает следующими особенностями:

а) жидкая фаза не имеет упорядоченной структуры, во всяком случае в областях, имеющих размеры более несколких межмолекулярных расстояний ( ~10^-9 м );

б) жидкая фаза устойчива для деформации растяжения-сжатия и абсолютно неустойчива относительно деформации сдвига, поэтому даже незначительная по величине сдвигающая сила приводит к перемещению слоев жидкости относительно друг друга;

в) вследствие последнего обстоятельства жидкости текучи, но практически несжимаемы.

Давление и вязкость в жидкой фазе

Как уже известно из курса физики, давление и вязкость газов обуслов-лены переносом импульса молекулами, находящимися в хаотическом тепло-вом движении. Подобные же процессы имеют место и в жидкостях. Учиты-вая, что свободного пробега молекулы в жидкости не существует, а ампли-туды тепловых колебаний связанных молекул на несколько порядков мень-ше, чем длина свободного пробега в газах, вклад этих процессов в перенос импульса мал. Однако, при увеличении температуры и приближении ее к

температуре испарения перенос импульса за счет теплового движения молекул возрастает. Давление в жидкости при температурах ниже тепературы испарения определяется действием внешних сил, в частности, силой тяжести. Давление p в точке объема покоящейся жидкости, находящейся в поле силы тяжести, на глубине h (рис. 6) - гидростатическое давление, определяется отношением веса столба жидкости F, находящейся выше заданной точки, к площади площад-

ки S, выделенной в этой точке (рис. 6). Т.е.

,

где - плотность жидкости;- ускорение свободного падения.

Аналогичное явление, конечно, наблюдается и в газах,

находящихся в поле силы тяжести. Однако, вследствие ма-

лой плотности газов гидростатическое давление в них становится существенным только при очень больших значениях h. Достаточно заметить, что давление, создаваемое на поверхности Земли многокилометровым столбом воздуха, равно давлению водяного столба высотой около 10м.

Передача гидростатического давления в различных направлениях определяется зконом Паскаля.

Закон Паскаля. Давление в любой точке покоящейся жидкости пере-

дается одинаково по всем направлениям (рис. 7).

Рассмотрим силы, действующие на куб со сторонойа, не содержащий жидкости и помещенный в жидкость с плотностью на глубинуот поверхности.

На боковые грани куба будут действовать

силы взаимно уравновешивающиеся. Сила, действующая на нижнюю грань, направлена вверх и равна. Сила, действующая на верхнюю граньнаправлена вниз. Результирующая сила равнаи направлена вверх. Из этих рассуждений следует закон Архимеда.

Закон Архимеда. На тело, погруженное в жидкость, действует выталкивающая сила равная весу вытесненной им жидкости.

Законы Паскаля и Архимеда справедливы и для газов.

Рассмотрим механизм проявления вязкости или внутреннего трения в жидкости. В газах сила внутреннего трения или вязкости определяется урав-нением Ньютона: , где- сила внутреннего трения;u – ско-рость направленного движения в каждой точке потока газа, движущегося в направлении координатной оси x; - поперечное изменение скорости на-правленного движения потока газа;- коэффициент динамической вязкос-ти. Производнаяобусловлена переносом проекции компоненты импуль-са направленного движения газа за счет теплового движения молекул. В жид-костях, вследствие отсутствия свободного пробега молекул, такой перенос невозможен. Однако, следует иметь ввиду, что в жидкостях молекулы отно-сительно сильно связаны взаимодействием ближнего порядка. Поэтому моле-кула, движущаяся в некотором направлении за счет внешней силы, будет

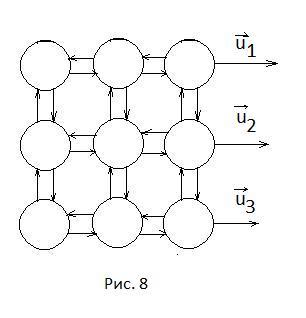
вовлекать в направленное движение другие молекулы, находящиеся в бли-жайшем окружении, за счет силы взаимодействия. Процесс вовлечения моле-кул жидкости в направленное движение со скоростью u представлен схема-тически на рис. 8. Стрелками условно обозначены силы притяжения-отталки-вания между молекулами.

Представим мысленный эксперимент, схема которого приведена на рис. 9. Внешняя сила F, необходимая для приведения в движение со ско-ростью u₀ верхней пластины, пропорциональна её площади S, скорости u₀ и обратно пропорциональна расстоянию d между подвижной и неподвижной

пластинами. Таким образом , где коэффициент пропорциональ-ности - динамическая вязкость жидкости. Если перейти к градиенту скорости , то для жидкости, также как для газа, получим уравнение Ньютона: .Сила внутреннего трения в жидкости пропорциональна поперечному градиенту скорости поступательного движения жидкости и площади контакта движущихся слоев.

Несмотря на кажущуюся идентичность законов, описывающих внутрен-нее трение в газах и жидкостях, они описывают явления с существенно раз-ными механизмами. Поэтому выводы, получаемые для газовой и жидкой фазы могут оказаться различными. В частности, в газах с увеличением тем-пературы усиливается взаимодействие движущихся слоев и коэффициент вязкости . В жидкостях же с увеличением температуры увеличивается расстояние между молекулами, вследствие чего уменьшается эффективность их взаимодействия и коэффициент вязкости быстро уменьшается в соответ-ствии с законом, гдеW – энергия взаимодействия молекул жидкости, препятствующая их сдвигу друг относительно друга; k - постоян-ная Больцмана.

В некоторых случаях вместо коэффициента динамической вязкости используется коэффициент кинематической вязкости равный.