Энергия гармонических колебаний

Сжимая или растягивая пружину, отклоняя маятник, мы совершаем работу против тех или иных сил. Эта работа должна превращаться в потенциальную энергию колеблющегося тела.

Потенциальная энергия определяется работой силы, вызывающей смещение х, в направлении силы F

dA=dE_п=-Fdx.

Учитывая, что F=-kx , получим dE_п = kx dx,

.

Подставим x=Asin(ω₀ t+φ₀) в выражение для Е_п

φ₀).

Учитывая, что k=mω₀², получим .

Кинетическая энергия колеблющегося тела

Полная энергия будет Е=Е_к+Е_п.

.

Математический и физический маятники

Математическим маятником называют идеализированную систему из нерастяжимой и невесомой нити с подвешенным на ней телом массойm, сосредоточенной в одной точке.

Тяжелый шарик, подвешенный на нити служит хорошим приближением к математическому маятнику (рис. 18). На отклоненный маятник будет действовать момент силы М

М=-mg ℓ sinφ.

Момент инерции шарика относительно точки подвеса J=ml².

Запишем уравнение динамики вращательного движения:

, или - mgl sin.

Сделав преобразования, получим

Известно, что для малых углов sin . Введем обозначение:

Подставляя их в вышеприведенное равенство , получим дифференциальное уравнение колебаний математического маятника

Решение этого уравнения имеет вид:

и является уравнением гармонического колебания математического маятника.

Здесь А – амплитуда, т.е. наибольший угол отклонения, α₀ – начальная фаза колебаний.

- период колебаний математического маятника.

Физическим маятником называют твердое тело, способное совершать колебания около неподвижной точки (оси), не совпадающей с его центром инерции .Вращающий моментM (рис.19)

M=-mgl sinφ

Уравнение динамики вращательного движе-

ния M=Jε :

-mgl sinφ=J.

Для малых углов считаем sin и тогда

-mglφ=J, или +=0.

Введем обозначение , и подставляя его в вышеприведенное равенство, получим дифференциальное уравнение колебаний физического маятника Решение этого уравнения: является уравнением гармонического колебания физического маятника. Период колебаний физического маятника

где l – расстояние между центром инерции и центром качания. Величину называют приведенной длиной физического маятника. С учетом этого, период колебаний физического маятника

Сложение гармонических колебаний. Векторная диаграмма гармонических колебанний

Возьмем на плоскости вектор А, который в момент времени t=0 составляет с горизонтальной осью угол α (рис.20).

Если этот вектор привести во вращение против часовой

стрелки с угловой скоростью ω₀,то проекция этого вектора на вертикальную ось х будет изменяться по закону x=Asin (ω₀t+α), т.е. по гармоническому закону в пределах от А до –А.

Следовательно, гармонические колебания можно представить в виде вращающегося вектора . Этим удобно пользоваться при рассмотрении сложения колебаний.

Сложение колебаний одинакового направления, одного периода, отличающихся начальной фазой и амплитудой .

Уравнения двух таких колебаний будут , .

На векторной диаграмме это будет выглядеть так, как показано на рис.21.

Результирующая амплитуда А будет определяться из выражения А²=A+A+2A₁A₂cos(α₁–α₂). Учитывая, что проекция суммы векторов равна сумме проекций слагаемых векторов, начальная фаза результирующих колебаний определится из ΔОВD:

Уравнение суммарного колебания будет

Проанализируем характеристики суммарного колебания:

1. Если разность фаз слагаемых колебаний

α₁α₂=±2πn(n=0,1,2,…), то сos α=1 и тогда А=А₁+А₂ , т.е. амплитуда результирующего колебания А равна сумме амплитуд слагаемых колебаний. Это будет условие максимума.

2. Если разность фаз α₁–α₂=±(2n+1) π (n=0,1,2,…), то сosα=-1 и тогда А=А₁–А₂. В случае, если А₁= А₂, колебания взаимно погасятся. Условие 2 является условием минимума .

3. Если А₁=А₂= А, а периоды и частоты мало отличаются , т.е. Т₁-Т₂=ΔТ«Т, то при сложении таких колебаний наблюдаются биения.

Вследствие небольшой разности периодов в некоторый момент времени колебания почти совпадают по фазе и амплитуды суммируются,

т.е. А₁ +А₂=2А.

При постепенном увеличении разности фаз наступает момент, когда колебания будут происходить в противофазе и А=А₁–А₂=0. Период биений, т.е. период огибающей (рис.22) определяется разностью частот слагаемых колебаний

Сложение взаимно перпендикулярных колебаний

1. Колебания имеют одинаковую фазу и частоту, но различные амплитуды.

Уравнения таких колебаний: x=A₁sin ωt. y=A₂sin ωt.

Разделим почленно левые и правые части уравнений и преобразуем полученное равенство

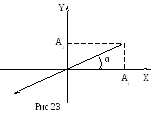
Получили уравнение прямой, проходящей через начало координат. Следовательно, результирующее движение осуществляется вдоль прямой, наклоненной к оси координат под углом α (рис.23), который определяется из условия

Результирующее колебание будет также гармоническим, т.к. смещение s определяется уравнением

2. Частоты колебаний равны, а фазы слагаемых колебаний отличаются на.

Уравнения таких колебаний имеют вид: x=A₁sin ωt, y=A₂sin(ωt+ )=A₂cos ωt.

Решим совместно эти уравнения .

Получили уравнения эллипса с осями А₁ и А₂ (рис. 24), т.е. траектория суммарного колебания представляет собой эллипс. При равенстве амплитуд траектория суммарного колебания представляет собой окружность. В общем случае сложение взаимоперпендикулярных колебаний траектория движения представляет собой фигуры Лиссажу.