Электрическое поле в диэлектрике

Если диэлектрик находится в однородном электрическом поле, то каждый внутренний элемент его объема ΔV является элек­трически нейтральным в силу того, что в этом ΔV- объеме положительные и отрицательные заряды компенсируют друг друга. В тонких слоях у поверхности диэлектрика в результате поляризации возникнут нескомпенсиро­ванные поверхностные заряды. У поверхности, в которую входят линии напряженности – отрицательные, из которой выходят – по­ложительные. Нетрудно показать, что поверхностная плотность этих заря­дов где Р – величина вектора поляризации диэлек­трика, α –угол между нормальюn к поверхности диэлектрика и на­правлением Е – вектора напряженности внешнего поля.

В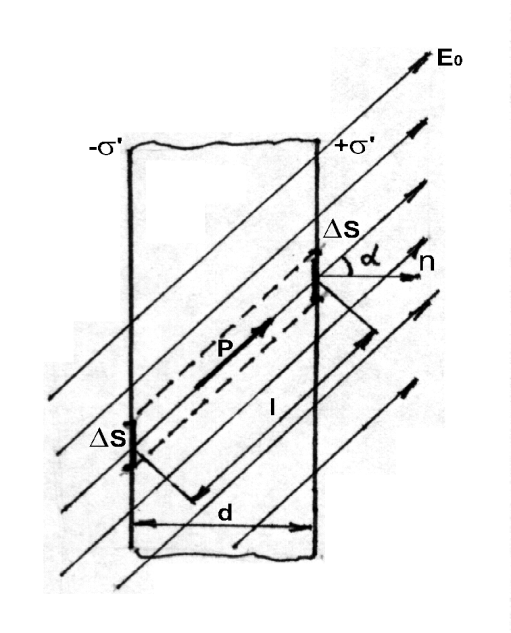озьмем плоскопараллельную пластину диэлектрика толщи­ной d и поместим ее во внешнее электрическое поле с напряженно­стью Е₀ так, что угол между n и Е₀ равен α (рис. 84).

Выделим мысленно объем в виде цилиндра с образующей, парал­лельной Е₀, и площадью основания ΔS. Величина этого объема

ΔV=ΔS·d =ΔS·l·cosα.

Объем ΔV имеет электрический дипольный момент, величина кото­рог о Р·ΔV=Р·ΔS·lcosα.

С другой точки зрения этот объем ΔV эквива-лентен элек­трическому диполю, образованному

электрическими зарядами +·ΔS и -ΔS, отстоя-

щими друг от друга на расстоянии l, и имею­ще- му дипольный момент равный ·ΔS·l.

Рис. 84

Приравняем эти два выражения для дипольного момента и получим

Р·ΔS·l·cosα =·ΔS·l,

Откуда

=Р·cosα=Р_n,

где Р_n – составляющая вектора поляризации по внешней нормали к поверхности. Выражая получим

где Е_n – нормальная составляющая напряженности поля внутри ди­электрика.

Возникающие в результате наложения внешнего поля Е₀ поверхностные заряды с поверхностной плотностью + и -будут создавать внутри диэлектрика собственное поле напряженностью. В результате чего напряженность Е суммарного электрического поля в диэлектрике будет (согласно принципу суперпозиции) равнаЕ = Е₀ + , или в скалярном виде Е = Е₀ - . НапряженностьЕ суммарного поля необходимо подставлять в формулу при вычислении связанных зарядов.

Так как напряженность Е электрических полей зависит от среды, в которой

возникает поле, то для расчета электрических по­лей (в особенности в диэлектриках) лучше пользоваться такой ха­рактеристикой поля как электрическое смещение D. Для диэлектри­ков выражение электрического смещения имеет вид D = ε₀ Е + Р. Подставляя , получим

D = ε₀ Е + =. Величинуназывают диэлектрической про-ницаемостью среды, а произведение ε·ε₀=ε_а называют абсолютной диэлектри­-

ческой проницаемостью среды.

D = ε ε₀ Е.

Пример расчета электрических полей в диэлектриках

Возьмем поле, образованное двумя бесконечными равно­мерно заряженными пластинами с поверхностной плотностью за­ряда σ и напряженностью Е₀ (рис.85).

Внесем в это поле пластину диэлектрика параллельно пластинам. На поверхностях диэлектрика появятся связанные заряды с поверх­ностной плотностью(рис. 85а). Эти заряды создадут внутри пла­стины однородное электрическое поле напряженностью. Вне диэлектрика напряженность этого поля=0. Оба поля направлены навстречу друг другу, следовательно внутри диэлектрика (рис. 85б)

,

откуда .

Величина ε показывает во сколько раз внешнее поле ослабляется за счет помещения в него диэлектрика. Умножив обе части последнего равенства на ε ε₀ , получим электрическое смещение D внутри пластины

D = ε ε₀ Е

Вне пластины электрическое смещение равно D = ε ε₀ Е, но ε = 1 и D = ε₀ Е₀ , т.е. электрическое смещение внутри и вне пластины одинаково.

Чтобы найти выразим:

;

, откуда .