Вектор индукции электрического поля. Поток векторов е и d

Рассмотрим, как меняется значение вектора Е на границе раздела двух сред, например, воздуха (ε 1) и воды (ε = 81). На­пряженность поля в воде уменьшается скачком в 81 раз. Такое по­ведение вектора Е создает определенные неудобства при расчете полей в различных средах. Чтобы избежать этого неудобства вводят новый вектор D – вектор индукции или электрического смещения поля. Связь векторов D и Е имеет вид

D = ε ε₀ Е.

Очевидно, для поля точечного заряда электрическое смещение будет равно

Нетрудно увидеть, что электрическое смещение измеряется в Кл/м², не зависит от свойств и графически изображается линиями, анало­гичными линиям напряженности.

Направление силовых линий поля характеризует направле­ние поля в пространстве (силовые линии, конечно, не существуют, их вводят для удобства иллюстрации) или направление вектора на­пряженности поля. С помощью линий напряженности можно характеризовать не только направление, но и величину напряженно­сти поля. Для этого условились прово­дить их с определенной густотой, так, чтобы число линий напряженности, про­низывающих единицу поверхности, пер­пендикулярной линиям напряженности, было пропорционально модулю вектора Е (рис. 78). Тогда число линий, пронизываю­щих элементарную площадку dS, нормаль к которой n образует угол α с вектором Е, равно E dScos α = E_n dS,

где E_n - составляющая вектора Е по направлению нормали n. Величину dФ_Е= E_ndS = EdS называют потоком вектора напряженности че­рез площадку dS (dS = dS·n).

Для произвольной замкнутой поверхности S поток вектора Е через эту поверхность равен

Аналогичное выражение имеет поток вектора электрического сме­щения Ф_D

.

Теорема Остроградского-Гаусса

Эта теорема позволяет определить поток векторов Е и D от любого количества зарядов. Возьмем точечный заряд Q и определим поток вектора Е че­рез шаровую поверхность радиуса r , в центре которой он располо­жен.

Для шаровой поверхности α = 0, cos α = 1, E_n = E, S = 4 πr² и

Ф_E = E · 4 πr².

Подставляя выражение для Е получим

Таким образом, из каждого точечного заряда выходит поток Ф_Е вектора Е равный Q/ ε₀ . Обобщая этот вывод на общий случай про­извольного числа точечных зарядов дают формулировку теоремы: полный поток вектора Е через замкнутую поверхность про­извольной формы численно равен алгебраической сумме электрических зарядов, заключенных внутри этой поверхно­сти, поделенной на ε₀ , т.е.

Для потока вектора электрического смещения D можно получить аналогичную формулу

поток вектора индукции через замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью.

Если взять замкнутую поверхность, не охватывающую заряд, то каждая линия Е и D будут пересекать эту поверхность дважды – на входе и выходе, поэтому суммарный поток оказывается равным нулю. Здесь необходимо учитывать алгебраическую сумму линий, входящих и выходящих.

Применение теоремы Остроградского-Гаусса для расчета элек­трических полей, создаваемых плоскостями, сферой и цилин­дром

1. Сферическая поверхность радиуса R несет на себе заряд Q, равномерно распределенный по поверхности с поверхностной плотностью σ

Возьмем точку А вне сферы на расстоянии r от центра и проведем мысленно сферу радиуса r симметричную заряженной (рис. 79). Ее площадь S = 4 πr². Поток вектора Е будет равен

По теореме Остроградского-Гаусса , следовательно,учитывая, чтоQ = σ·4 πr², получим

Для точек, находящихся на поверхности сферы (R = r )

Для точек, находящихся внутри полой сферы (внутри сферы нет за­ряда), Е = 0.

2. Полая цилиндрическая поверхность радиусом R и длиной l заряжена с постоянной поверхностной плотностью заряда (Рис. 80). Проведем коаксиальную цилиндрическую поверхность радиусаr > R.

Поток вектора Е через эту поверхность

По теореме Гаусса

Приравнивая правые части приведенных равенств, получим

.

Если задана линейная плотность заряда цилиндра (или тонкой нити) то

3. Поле бесконечных плоскостей с поверхностной плотно­стью заряда σ (рис. 81).

Рассмотрим поле, создаваемое бесконечной плоскостью. Из сооб­ражений симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости.

В симметричных точках Е будет одинакова по величине и противоположна по направлению.

Построим мысленно поверхность цилиндра с основанием ΔS. Тогда через каждое из оснований цилиндра будет выходить поток

Ф_Е = Е ΔS, а суммарный поток через цилиндрическую поверхность будет равен Ф_Е = 2Е ΔS.

Внутри поверхности заключен заряд Q = σ · ΔS. Согласно теореме Гаусса должно выполняться

откуда

Полученный результат не зависит от высоты выбранного цилиндра. Таким образом напряжённость поля Е на любых расстояниях одинакова по величине.

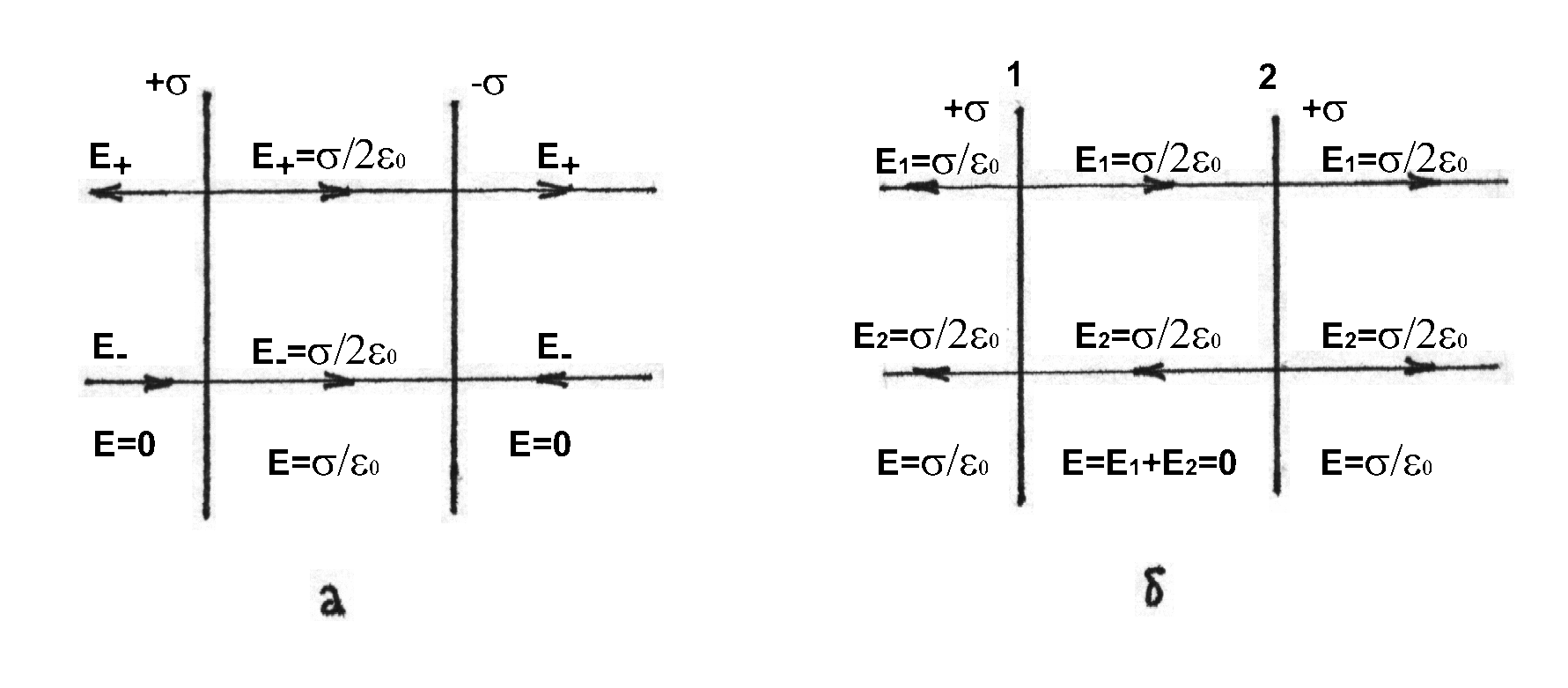
Рис. 82

Для двух разноименно заряженных плоскостей с одинаковой по­верхностной плотностью заряда σ по принципу суперпозиции вне про­странства между плоскостями напряжённость поля равна нулю Е = 0, а в пространстве между плос­костями (рис. 82а). В случае, если плоскости заряжены одноименными зарядами с одинаковой поверхностной плотностью зарядов, наблюдается об­ратная картина (рис. 82б). В пространстве между плоскостями Е=0, а в пространстве за пределами плоскостей.