Закон Ома в дифференциальной и интегральной форме

Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно про­порциональна сопротивлению R

.

Закон Ома можно представить в дифференциальной форме. Через поперечное сечение проводника течет ток силой dI равной dI = jdS. Напря- жение, приложенное на концах проводника, будет равно Е·dl (т.к. и dφ = -Edl). Для проводника постоянного сече­ния длиной l будем иметь

.

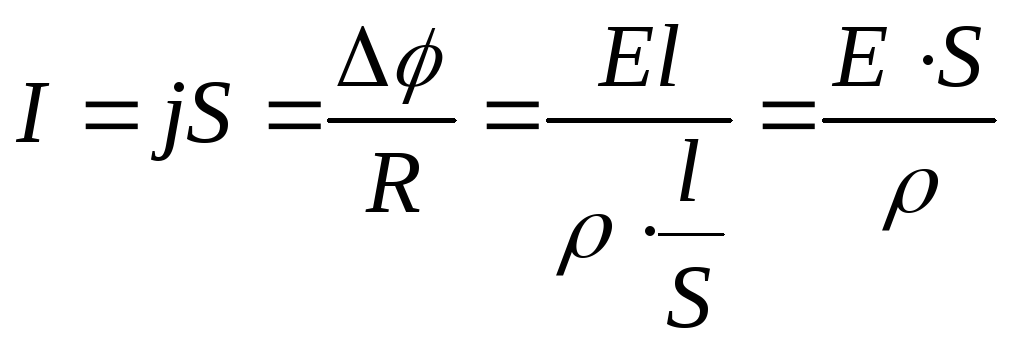Отсюда , где- удельная проводимость проводника. Таким образом, выражениезакона Ома в дифференциальной форме в векторном виде будет

j = γ E.

Плотность тока в проводнике прямо пропорциональна напряженно­сти электрического поля в нем.

Рассмотрим замкнутую электрическую цепь, содержащую ЭДС. Источник тока в такой цепи обладает внут­ренним сопротивлением r. Сопротивление внешней части цепи R называют внешним или сопротивлением нагрузки. Падение напря­жения на внутреннем участке цепи равно U₁ = Ir, а на внешнем - U =IR. При замкнутой внешней цепи ЭДС источника тока ؏ равна сумме падений напряжения на внутреннем сопротивлении источ­ника тока и во внешней цепи, ؏ = Ir + IR, откуда

I = ؏ / (r + R).

Это есть выражение закона Ома в интегральной форме.

Закон Джоуля-Ленца в дифференциальной и интегральной форме

Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предполо­жим, что на концах участка проводника имеется разность потен­циалов U = φ₁ – φ₂.

Тогда работа по переносу заряда q на этом участке равна

A = q(φ₁ – φ₂) = qU.

Если ток постоянный, то иA = I U t.

Эта работа равна количеству теплоты Q и формула Q = I U t вы­ражает закон Джоуля-Ленца в интегральной форме.

Используя выражение закона Ома получим

.

Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

,

где S - сечение, l - длина проводника. Подставляя Q = I² R t и , получим .

Здесь - плотность тока,, и учитывая, чтоj = γE, получим

.

Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удель­ная проводимость проводника.

Вывод законов Ома и Джоуля-Ленца из классических электрон­ных представлений

Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·10⁶ Кл. Взвешивание показало неизменный вес цилинд­ров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.

Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.

Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти час­тицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет пе­ренесен некоторый заряд.

Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с прово­дом вокруг ее оси. К концам катушки подключили телефон, в кото­ром был слышен звук, обусловленный импульсами тока. Был полу­чен качественный результат – зарегистрирован импульс тока.

Толмен и Стюарт в 1916 г. получили количественный ре­зультат. Катушка с проводом длиной 500 м приводилась во враще­ние со скоростью v=300 м/с. Катушка резко тормозилась и с по­мощью баллистического гальванометра измеряли заряд, протекав­ший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m полу­чалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электро­проводности металлов в предположении, что:

- электроны в металле ведут себя подобно молекулам иде­ального газа;

- движение электронов подчиняется законам классической механики;

- взаимодействие электронов сводится к соударениям с ио­нами кристалли-ческой решетки;

- силами взаимодействия между электронами можно пре­небречь и они между собой не сталкиваются;

- электроны в отсутствие электрического поля движутся хаотически.

Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.

По определению плотность тока j = n e <v> - это заряд, переносимый через единицу площади S = 1м² за единицу времени t=1 с; n – концентрация электронов, е – заряд элек­трона, <v> - средняя скорость упорядоченного движения электро­нов.

На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение и к концу свободного про­бега он достигнет скорости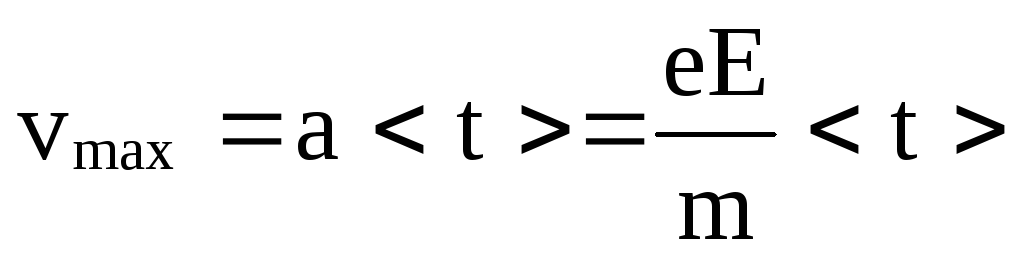, а средняя скорость <v>=v_max/2.

Если <v_T> - средняя скорость теплового хаотичного движе­ния электронов, а средняя длина свободного пробега электронов <λ>, то среднее время между соударениями <t> = . Подставляя <t> в формулу для <v> получим:

.

Подставляя <v> в формулу для j, получим

,

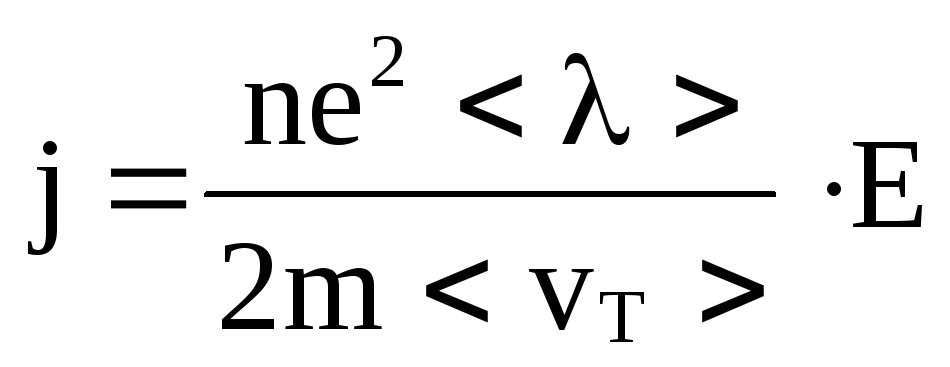т.е. плотность тока прямо пропорциональна Е, а это и есть выраже­ние закона Ома в дифференциальной форме. Если положить, что

то j = γ E.

Удельная проводимость γ ~ n и < λ>, <v_т> ~ T, поэтому проводимость снижа­ется с ростом температуры, а удельное сопротивление по­вышается с ростом температуры. К концу свободного пробега электрон приоб­ретает кинетическую энергию

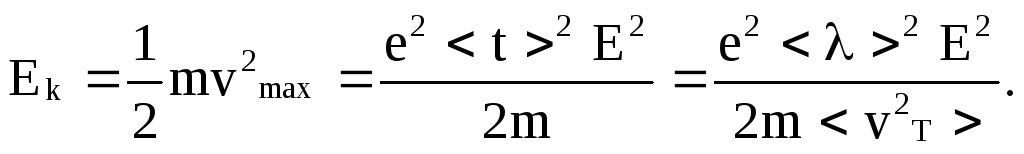
Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон ис­пытывает <v_T>/ < λ > cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в еди­нице объема за единицу времени выделится количество тепла

.

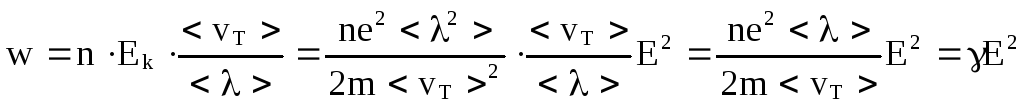Таким образом, - выражение закона Джоуля-Ленца в дифференциальной форме.