Структура населения г. Москвы

Рис.2.4. Ленточная диаграмма распределения населения г. Москвы по половозрастному составу

В отличие от столбиковых и ленточных диаграмм в круговых, квадратных, прямоугольных и треугольных диаграммах величина изображаемого явления выражается размером площади, которая отводиться этому показателю на поле графика, а сами графики строятся тоже по определенным правилам.

Например, для построения квадратной диаграммы для графического сравнения общего размера площади однокомнатной (35,2 м²) и двухкомнатной (46,4 м²) квартир вначале извлекаем квадратный корень из сравниваемых величин (получаем 5,9 и 6,8), затем выбираем масштаб (примем 1см за 2 м²) и отмечаем на графике стороны квадратов, пропорциональные полученным числам (рис. 2.5).

Рис.2.5. Квадратная диаграмма сравнения общей площади квартир

Круговые диаграммы, используемые для сравнения показателей, строят по тем же правилам. Разница лишь в том, что на графике вычерчиваются круги, площади которых пропорциональны квадратным корням из изображаемых величин и при построении учитывается радиус окружности.

В треугольной диаграмме нужно так выбрать стороны и высоту треугольника, чтобы его площадь соответствовала величине показателя.

В качестве знаков для графика можно применять фигуры. Размер рисунка должен соответствовать величине показателя. Фигурные или картинные диаграммы (пиктограммы) усиливают наглядность изображения, так как включают рисунок изображаемого показателя (рис. 2.6).

Структурные диаграммы характеризуют состав статистических совокупностей. Наиболее распространенным способом графического изображения структуры статистической совокупности является секторная диаграмма (рис. 2.7). При ее построении вся совокупность и соответствующая ей общая площадь круга принимается за 100%. Круг разбивается на секторы пропорционально частям совокупности. Поскольку на 1% приходится 3,6°, то для изображения любой части целого необходимо ее процентное выражение умножить на 3,6°.

Потребление кофе на душу населения, кг

Австрия Нидерланды

Швейцария Германия

Франция США

Россия

Рис.2.6. Фигурная диаграмма потребления кофе на душу населения

Структура возрастного состава населения г. Москвы

Рис.2.7. Секторная диаграмма распределения населения г. Москвы по возрасту

Диаграммы динамики используются для изображения явлений, протекающих во времени. Наиболее часто в данном случае используются линейные диаграммы (рис. 2.8).

Для построения линейных диаграмм обычно применяется прямоугольная система координат. На оси абсцисс откладываются варианты изучаемого показателя (или показания времени), а на оси ординат  величины изучаемого показателя. Зная эти координаты, легко определить положение каждого уровня на поле графика в виде соответствующей точки. Точки в линейных диаграммах являются геометрическими знаками. Последовательно соединяя найденные точки отрезками линий, получают эмпирическую линию графика, называемую статистической кривой. По виду этой линии можно судить о тенденциях и особенностях развития изучаемого явления в пространстве или во времени.

Рис.2.8. Линейная диаграмма динамики производства муки в России за 1965  2005 гг.

Разновидностью линейной диаграммы являются радиальные диаграммы, построенные в полярной системе координат. Они применяются для отражения процессов, неоднократно повторяющихся во времени, и бывают двух видов замкнутые и спиральные.

При построении таких диаграмм изображается окружность, которая делится на несколько равных частей по числу отрезков времени. Полученные точки деления соединяются с центром круга радиусами. На каждом радиусе в соответствии с выбранными промежутками времени и масштабом откладываются значения изучаемого показателя и полученные точки соединяются отрезками прямой. Получается ломаная линия, которая позволяет проследить динамику изучаемого явления.

Рассмотрим построение радиальной замкнутой диаграммы на условном примере.

Объем производства кондитерских изделий в РФ в 1995г. составил (тыс. т):

Месяц	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
Объем производства	92	110	124	125	114	111	96	108	116	122	120	124

Делим круг на 12 частей (соответственно числу месяцев в году), на радиусах согласно масштабу делаем отметки исходя из приведенных данных за каждый месяц. Получаем ломаную линию, которая позволяет проследить динамику изучаемого явления в течение года (рис. 2.9).

Производство кондитерских изделий в РФ по месяцам года

Рис.2.9. Радиальная замкнутая диаграмма производства кондитерских изделий в РФ по месяцам года

Спиральная радиальная диаграмма строится в том случае, если имеются помесячные статистические данные за ряд лет. Принцип ее построения тот же, что и замкнутой диаграммы, но в ней декабрь одного года соединяется с январем не того же года, а с январем следующего года, так что получается кривая в форме спирали.

Линейные диаграммы используются также для изображения рядов распределения и характеристики вариации их значений. В этом случае применяют такие диаграммы, как полигон распределения, кумулята (кривая "меньше, чем") и огива (кривая " больше, чем").

Полигон распределения строят в основном для изображения дискретных вариационных рядов. Он представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами  соответствующие им частоты или частости. Крайние точки полученного графика соединяют с точками по оси абсцисс, отстающими на одно деление в принятом масштабе от минимального и максимального значения вариант.

Построим полигон по данным о распределении квартир жилого дома по числу проживающих в них (рис 2.10).

Число проживающих в квартире человек 1 2 3 4 5 6 7 Всего

Число квартир 2 3 10 23 9 2 1 50

Полигон может быть построен и для интервального вариационного ряда, для этого в качестве координат по оси абсцисс используют середины интервалов. Но чаще всего для изображения интервальных рядов распределения используют гистограммы, в которых основания столбцов равны величине интервалов, а высота столбцов соответствует их частоте.

Рис.2.10. Полигон распределения квартир жилого дома по числу проживающих человек

Гистограмма может быть преобразована в полигон распределения, если найти середины верхних сторон прямоугольников и затем эти точки соединить прямыми линиями. При этом середины сторон крайних прямоугольников соединяют с осью абсцисс в точках, отстоящих в принятом масштабе на величину интервалов от середины первого и последнего интервалов.

Построим гистограмму и полигон по данным о распределении работников фирмы по уровню доходов (рис. 2.11):

Группы работников по уровню дохода, тыс. руб.	Число работников, чел.
До 5,0 5,0 – 10,0 10,0– 15,0 15,0 и более	30 60 15 10
Итого	115

Рис.2.11. Гистограмма и полигон распределения работников фирмы по уровню дохода

При построении кумулятивной кривой или кумуляты вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты (частости), которые определяют последовательным суммированием частот (частостей) ряда. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.

Построим кумулятивную кривую для рассмотренного выше примера распределения квартир по числу проживающих (рис. 2.12).

Число проживающих в квартире человек 1 2 3 4 5 6 7 Всего

Число квартир 2 3 10 23 9 2 1 50

Накопленные частоты 2 5 15 38 47 49 50 -

Рис.2.12. Кумулятивная кривая распределения квартир по числу проживающих

При построении кумулятивной кривой для интервального вариационного ряда на оси абсцисс откладываются варианты ряда, а на оси ординат  накопленные частоты. При этом нижней границе первого интервала соответствует нулевая частота, верхней – частота всего интервала; нижней границе второго интервала соответствует частота первого интервала, а верхней – накопленная частота первого и второго интервала и т.д. Верхней границе последнего интервала, таким образом, должна соответствовать сумма всех частот ряда, что соответствует общей численности изучаемой совокупности.

При построении огивы вариационного ряда по оси абсцисс откладываются накопленные частоты, а по оси ординат – варианты ряда.

Построим огиву для ряда распределения квартир по числу проживающих (рис. 2.13).

Рис.2.13. Огива ряда распределения квартир по числу проживающих

В экономической практике для сопоставления трех величин, из которых одна является произведением двух других, нередко применяются диаграммы под названием "знак Варзара"  это прямоугольник, у которого один сомножитель принят за основание, другой  за высоту, а вся площадь равна произведению (рис. 2.14). Так можно изобразить, например, размер посевной площади пшеницы в стране, величину урожайности и величину валового сбора в определенном году, а также, например, цену, количество продукции в натуральном выражении и выручку от реализации продукции (объем продаж).

Рис.2.14. Знак Варзара, отображающий объем продаж

Статистические карты в свою очередь делятся на картограммы и картодиаграммы.

На картограмме распределение изучаемого признака по территории изображается условными знаками (точками, штриховкой, цветом и т.д.), соответствующими определенной интенсивности значений величины этого признака. Эти знаки покрывают площадь каждого района. Картограмма применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака между отдельными районами для выявления закономерностей этого распределения (рис. 2.15).

Картограммы бывают фоновые и точечные. На фоновых картограммах распределение изучаемого явления на территории изображается различными окрасками территориальных единиц с разной густотой цвета или штриховкой различной интенсивности. Чем более интенсивно явление, тем гуще штриховка или темнее окраска. Такие картограммы обычно используются для изображения уровня относительных и средних величин по территориям.

На точечной картограмме символами графического изображения статистических данных являются точки. Точечная картограмма применяется для размещения абсолютных величин. Каждой точке, нанесенной на картограмму, придается числовое значение, что позволяет использовать ее для прямого счета. Например, имеются четыре района с добычей угля в 200, 500, 1000 и 1400 тыс. т в год. Для составления картограммы примем точку за 100 тыс. т и нанесем на контур каждого района соответствующее количество точек.

Картодиаграмма — это сочетание диаграммы с географической картой. В качестве изобразительных знаков в картодиаграммах используются те или иные фигуры, которые размещаются на самой географической карте (рис. 2.16).

Картограммы дают возможность графически отразить более сложные статистико-географические соотношения, чем картограммы. Так, при помощи картодиаграммы можно выразить пространственную специфику в структурах изучаемых статистических совокупностей, особенности каждого района как единого целого и т.д. В качестве диаграммных знаков в картодиаграмме часто используют различные геометрические фигуры, особенно круги, которые наиболее просты и удобны для выражения сравниваемых количественных показателей на карте.

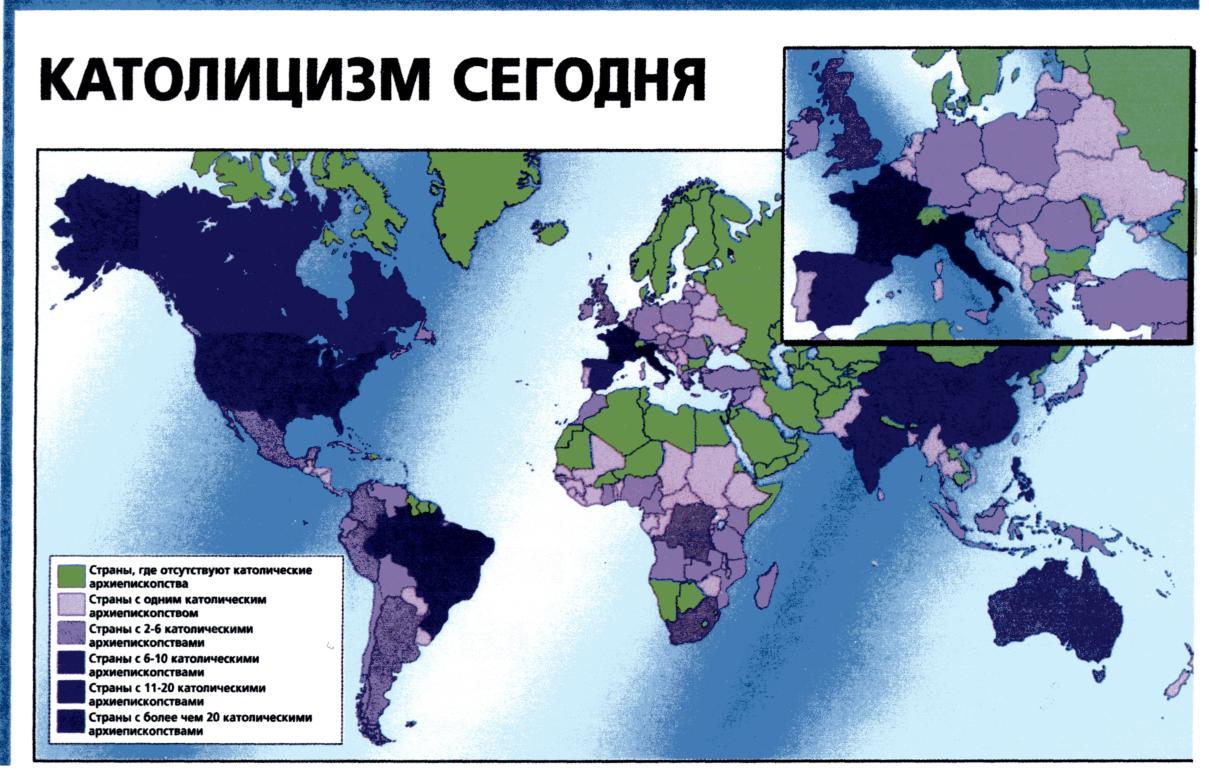
Рис.2.15. Картограмма территориального распределения католицизма по странам мира

Рис.2.16. Картодиаграмма стран-производителей золота и серебра