3.2. Авторегрессия, автокорреляция

Пусть задан ряд значений:

u₁, u₂,...,u_m.

Если предшествующие члены этого ряда находятся в зависимости с последующими в момент t, мы имеем дело с авторегрессионной моделью.

В общем виде авторегрессионная модель имеет вид:

u_t = f (u_t-1, u_t-2,..., u_t-m).

Линейный ее вариант можно записать в следующем виде:

u_t = ₁u_t-1 + ₂u_t-2 +...+ _mu_t-m + _t,

где _t - малая величина;

m - число членов, которое охватывает автокорреляционная модель (порядок автокорреляции).

Очевидно, что (u₁, u₂); (u₂, u₃);...; (u_m-1, u_m) образуют множество двухмерных величин с соответствующими коэффициентами корреляции стандартного типа.

Однако другие пары, в частности (u₁, u₃); (u₂, u₄); (u₃, u₅) и т.д. тоже образуют множество двухмерных величин, но в отличие от первого они образуют сериальные коэффициенты корреляции порядка k, т.е. r_k.

Итак, если имеется функция

y_t = f(y_t-1, y_t-2,..., y_t-k),

то в этом случае для характеристики взаимосвязи используются так называемые авторегрессионные модели.

Линейный ее аналог имеет вид:

y_t = ₁y_t-1 + ₂y_t-2 +...+ _my_t-m.

Расчет коэффициента автокорреляции имеет вид:

;

где ;

Аналогично, коэффициент автокорреляции второго и более высоких порядков:

;

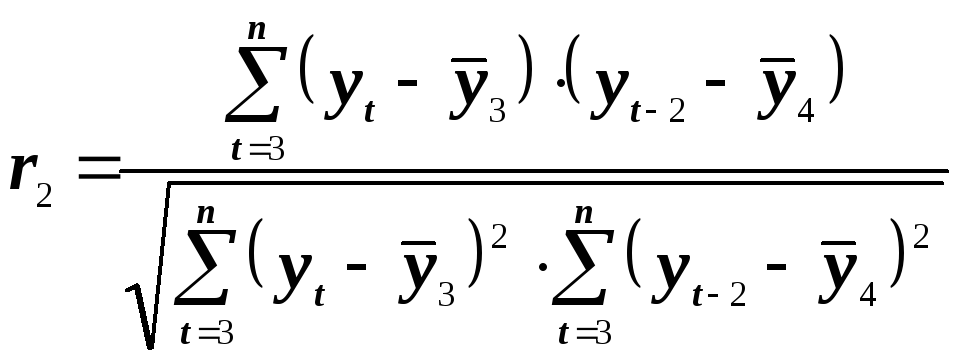где ;

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины Лага, принято называть коррелограммой.

3.3. Динамические модели прогнозирования

Интерес к будущему возникает из непосредственной и острой практической потребности. Необходимость предвидения вероятного исхода отдельных экономических составляющих, в частности, спроса, предложения, стоимостных показателей, емкости рынка и т.д. особенно важна для бизнесменов, предпринимателей, менеджеров и т.п.

Предвидение событий позволяет заблаговременно приготовиться к ним, учесть их положительные и отрицательные последствия, а если есть возможность, то вмешаться в ход развития, контролировать его и, что более важно исследовать альтернативы будущего состояния.

Процессу прогнозирования предшествует аналитическая оценка исходной системы. Она должна производиться на основе охвата комплекса внутренних и внешних факторов. Затем происходит процесс прогнозирования, следовательно, и прогностическая оценка показателей.

Как правило, процесс прогнозирования осуществляется на основе формул:

1. y = a + bt

2. y = a + bt + ct²

3. y = a + bt + ct² + dt³ и т.д.

В зависимости от исходной информации прогнозирование может осуществляться на основе нижеприведенных формул:

y_t = ab^t.

Путем преобразования получаем:

.

;

;

.

В итоге:

.

Прогнозирование также может осуществляться на основе следующих формул:

или

;

;

;

и другие.

3.4. Гомоскедастичноость, гетероскедастичность остатков

Как упоминалось, при оценке параметров уравнения регрессии применяется метод наименьших квадратов. При этом делаются определенные предпосылки относительно случайной составляющей ε.

В модели

у = а + а₁х₁ + а₂х₂ + … + а_кх_к+ ε

случайная составляющая ε представляет собой ненаблюдаемую величину. Задача заключается в том, чтобы одновременно исследовать случайную величину ε_i.

В предыдущих разделах мы остановились на формальных проверках статистической достоверности коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента, F-критерия Фишера. При использовании этих критериев делаются предположения относительно поведения остатков ε_i. Утверждалось, что остатки представляют собой независимые случайные величины.

Затем осуществляется исследование остатков. Предусматривается следующие пяти предпосылок:

- случайный характер остатков;

- нулевая средняя величина остатков, не зависящая от х_i;

- гомоскедастичность - дисперсия каждого отклонения ε_i одинакова для всех значений х;

- остатки ε_i не имеют постоянной дисперсии;

- остатки ε_i носят систематический характер.

Итак, в соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_j остатки ε_i имеют одинаковую дисперсию. Если это условие не соблюдается, тогда имеет место гетероскедастичность.