1.6.6. Дробно-рациональные функции

Для оценки технико-экономических показателей также может применяться дробно-рациональные функции. Рассмотренная выше функция является частным случаем дробно-рациональной функции.

Дробно-рациональная функция имеет вид:

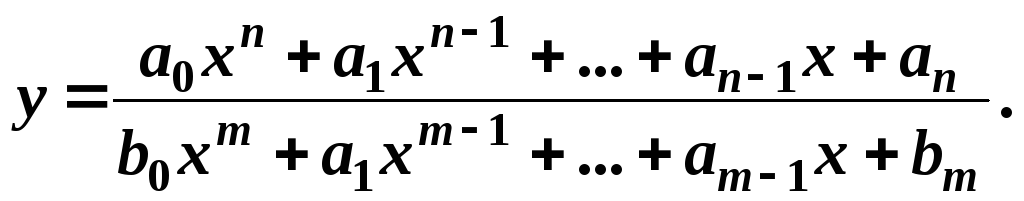
Пример 1. Предположим, имеется функция следующего вида:

После преобразования получим:

Из этого следует, что прямые х = 1, х = 2 являются двусторонними (вертикальными) асимптотами графика.

Теперь определим точки максимума и минимума. Предположим, что

или

следовательно:

Чтобы прямая у = а пересекла график в двух совпадающих точках, необходимо, чтобы

а² + 6а + 1 = 0

Следовательно:

Это и есть два экстремальных значения функции. Соответствующие им значения аргумента получаем из равенства

Следовательно:

Таким образом, функция имеет максимум, приминимумприГрафик функции представлен на рис. 8.

Рис. 8

Пример 2. Исследовать и построить график функции:

х² + 1 > 0 при любом х, функция определена на всей числовой оси. Если х = 0, то у = 1, следовательно, график пересекает ось ординат в точке (0,1).

Если х = -1, то у = 0. т.е. график пересекает ось абсцисс в точке -1.

Теперь найдем экстремальные значения функции. Для этого следовало бы найти точки пересечения данной кривой с прямой у = а.

ах² – х – 1 + а = 0

Следовательно,

Далее, путем приравнивания к нулю дискриминанта определим экстремальные значения функции:

1+ 4а - 4а² = 0

.

Итак, ,

Точка есть точка максимума, а точка- минимума.

Для уточнения графика определим еще несколько точек. Если х = 1, то у = 1, если х = 2, то у = 0,6; если х = -2, то График изображен на рис. 9.

Рис. 9

Пример 3. Исследовать и построить график функции

Область определения функции состоит из двух интервалов: (-∞, 1) и (1, + ∞). Это значит, что график функции состоит из двух ветвей:

.

Найдем точки экстремума. Для этого полагаем, что , следовательно:

Затем, приравнивая дискриминант нулю, получим экстремальные значения функции:

.

Следовательно, .

Таким образом, функция имеет минимум в точке, равной, максимум в точке, равной.

График функции изображен на рис. 10.

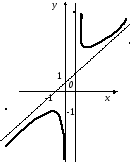
Рис. 10

1.6.7. Степенная функция

Функция вида

у = х^п,

где п – любое число, называется степенной.

1.6.7.1. Степенная функция с натуральным показателем

В данном случае область ее определения является вся числовая ось.

Если п – четное число (п = 2к), то х^п – четная функция, так как (-х)^2к = х^2к.

Если п – нечетное число, т.е. п = 2к - 1, то х^п – нечетная функция, так как (-х)^{2к -1} = х^{2к - 1}.

Функция у = х^п (при любом натуральном п) является возрастающей в интервале (0, +∞).

Иллюстрация этого служат графики функции у = х² , у = х³ (рис. 11 и 12.).

Рис. 11 Рис. 12

1.6.7.2. Степенная функция с целым отрицательным показателем

По определению

.

Легко убедиться, что в интервале (-∞, 0) функция возрастает, еслиn – четное, и убывает, если n нечетное.

Иллюстрацией также могут служить графики функций(рис. 13) и(рис. 14).

Рис. 13 Рис. 14