1.6. Наиболее привлекательные функции для измерения экономических процессов (спроса, выпуска продукции, ценообразования и других)

Для количественной оценки технико-экономических показателей, в частности спроса, предложения (выпуска продукции) и других возможно применение не только линейных, но и различных более усложненных функций.

1.6.1. Квадратичная функция

Зависимость между спросом и насыщенностью потребительского рынка вполне может выражаться функцией вида:

y = aх² + bx + с,

где х - насыщенность рынка;

у - спрос;

а, b, с - параметры системы.

Предположим, что b = 0, с = 0. Тогда функция примет вид:

y = ax².

График, последней функции в зависимости от величины коэффициентов а - принимает вид

Рис. 2

Осуществим преобразования функции:

Итак,

Первая часть равенства есть сумма двух слагаемых, из которых зависит от переменнойх, не зависит отх, следовательно, имеет постоянное значение.

Чтобы получить график функции , имея графику = ах², достаточно сдвинуть график у = ах² вдоль оси абсцисс на отрезок, равный , а затем достаточно произвести перенос вдоль оси ординат на величину.

Т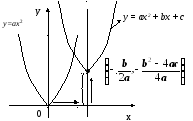аким образом, чтобы получить график функцииу = ах² + bx + c надо сдвинуть график у = ах² сначала вдоль оси абсцисс на отрезок , а затем вдоль оси ординат на. На рис. 3 показаны графики функцииу = ах² + bx + c:

Рис. 3

1.6.2. Биквадратная функция

Функция вида

у = ах⁴ + bx² + c (а ≠ 0)

называется биквадратной.

После преобразования получим:

Если b ≠ 0, то график функции получается либо из графика функции у = х⁴ + х², либо из графика у = х⁴ - х².

График функции у = х⁴ + х², есть сумма графиков функции у = х⁴, у = х². На рис. 4 показан график данной функции:

Рис. 4.

1.6.3. Кубическая функция

Функция вида у = ах³ + bх² + cx + d, где a ≠ 0, b, c и d - любые числа, называется кубической. В зависимости от конкретных обстоятельств данную функцию также возможно использовать для оценки основных технико-экономических показателей, и в том числе спроса, предложения, равновесных цен и других.

Функция у = х³. Если а = 1, b = c = d = 0. В данном случае график функции имеет вид:

Рис. 5.

1.6.4. Обратно пропорциональная функция

При оценке технико-экономических показателей особый интерес представляют функции обратно пропорциональной зависимости.

Функция, заданная равенством

,

называется обратно пропорциональной. Графики представлены на рис. 6а, 6б, 6в.

Рис. 6 а Рис. 6б

Рис. 6в

К семейству обратно пропорциональных функций относятся:

и другие.

Данные типы функции наиболее привлекательными являются для оценки зависимости между спросом и насыщенностью потребительского рынка, между спросом и рентабельностью производства и т.д.

1.6.5. Дробно-линейная функция

Дробно-линейной функцией называется функция, заданная равенством:

,

где числитель и знаменатель — линейные функции.

Преобразуем заданную функцию.

Из последнего следует, что график дробно-линейной функции — представляет собой гиперболу с асимптотами и

Пример. Построить график функции

Преобразуем данное уравнение:

Таким образом, для построения графика данной функции надо построить график функции , а затем сдвинуть его вверх вдоль оси ординат на три единицы (рис. 7).

Рис. 7