3.8. Упрощенное оценивание параметровмодифицированной экспоненты, кривой Гомперца и логической кривой

Если нет полного ряда данных, в этих обстоятельствах оценки параметров функции, возможно на основе трех точек.

3.8.1. Метод трех сумм

Предположим, имеется функция:

Для этой функции выявлены следующие формулы:

;

;

.

Таким образом, сперва определяется параметр b, затем а и наконец К. Если в последнее выражение подставить найденные выше значения а и b, то К можно определить следующим образом:

.

Значение К лучше определять на основе последней формулы, поскольку в этом случае не будет сказываться округление параметров а и b. Малейшее изменение их обычно существенно влияет на величину К.

Пример. Пусть уровни ряда формируются по закону К + аb^t, причем К = 120, а = -60, разность между асимптотой и у₀, в отношение последовательных первых разностей ординат.

Итак, у_t = 120 – 60 ∙ 0,5^t.

Продолжим эксперимент. Пусть на показатели ряда воздействуют некоторые случайные факторы, причем соответствующие случайные сдвиги составляют не более 5%.

Воспользовавшись таблицей случайных чисел для определения возмущения (∑_t) получим следующие данные (таблица 3).

Таблица 3

Генерирование данных (модифицированная экспонента)

t	120 – 60 ∙ 0,5t	∑t	yt
1	60	+2,5	62,4
2	90	+4,8	94,8
3	105	-6,0	99,0
4	112,5	+6,0	118,5
	367,5		374,7
5	116,25	-1,2	115,05
6	118,12	+3,5	121,72
7	119,06	-2,4	116,82
8	119,53	+2,5	122,20
	472,96		475,79
9	119,77	+2,4	122,17
10	119,88	+1,2	121,08
11	119,94	-4,8	115,14
12	1119,97	0	119,97
	479,56		478,36

Определим теперь значения параметров а и b, К на основе данных таблицы:

;

;

.

В итоге имеем

у_t = 114 – 38,8 ∙ 0,35^t.

Итак, метод трех сумм "работоспособен" в сравнительно узких пределах колебаний исходных данных, а результаты весьма чувствительны к случайным возмущениям.

Рассмотрим метод трех сумм к оценке параметров кривой Гомперца. Напомним, что с помощью логарифмирования кривую Гомперца легко представить в виде модифицированной экспоненты

ℓog a + ℓog K + bt ℓog a

Пользуясь рассмотренным методом определения параметров модифицированной экспоненты, получим:

;

;

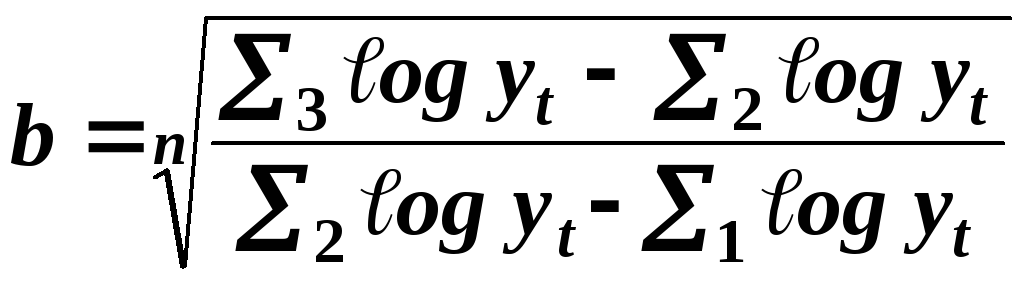или

.

Аналогичный подход возможен при оценке логистической кривой, вида:

,

;

;

или

.

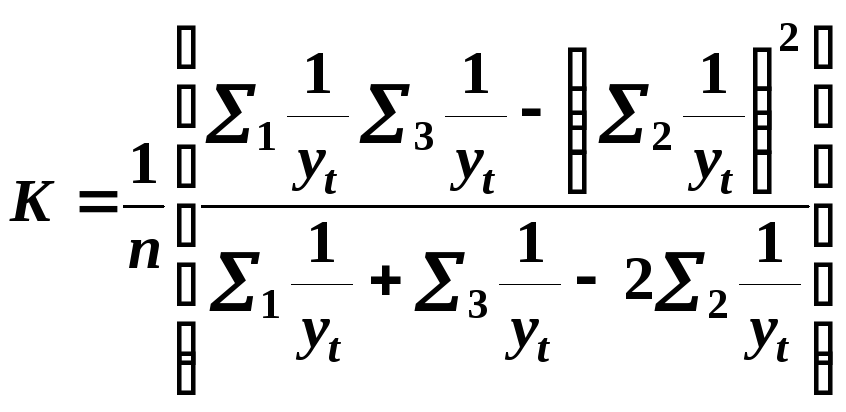Если логистическая кривая имеет вид:

,

то метод трех сумм для оценки параметров можно применить следующим образом. Пусть, как и выше, ряд разбит на три части:

; ;.

тогда

;

;

.

где

.

Определим теперь разности:

;

.

Отсюда отношение разностей составит:

.

Таким образом,

.

Имеем,

.

После преобразования получим:

Поскольку:

;

получим:

.

3.8.2. Метод трех точек

Предположим, задана логическая кривая -

.

Здесь, также:

;

;

.

Определим параметр а из первого уравнения системы, получим:

Отсюда

,

.

Параметр b найдем из второго уравнения системы, одновременно подставив вместо 10а соответствующее выражение, получим:

.

Отсюда следует, что имеем:

.

Наконец,

.

Подставив в это выражение 10а и 10bn, после соответствующих преобразований, получим:

.

Пример. Предположим, что необходимо провести логическую кривую через три точки. Пусть у₀ = 12,9; у₁ = 62,1; у₂ = 152,7. Интервалы у₀-у₁ и у₁-у₂ равны 6 единицам времени, тогда

;

;

.

Таким образом,

Аналогичным образом находятся параметры логистической кривой вида:

.

Три точки, через которые надо провести кривую можно определить следующим образом:

;

;

Определим теперь разности d₁, d₂:

;

.

Отсюда

.

Итак, .

Определим значение выражения. После преобразований получим:

.

Отсюда

.

Следовательно:

.

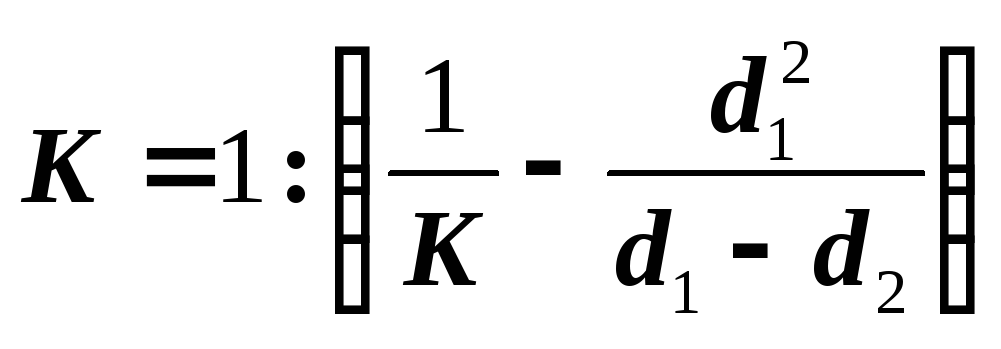Наконец, из первого уравнения системы получим:

.

Для иллюстрации вернемся к рассмотренному примеру, где у₀ = 12,9; у₁ = 62,1; у₂ = -152,7, n = 6. На основе этих данных получим:

; ;;

d₁ = 0,06142; d₂ = 0,00955;

,

К = 208,2;

.

Таким образом,

Рассмотренный метод оценки параметров весьма прост, однако он очень чувствителен к величине значений у₀, у₁, у₂, которые даже если они получены усредненным путем, могут содержать существенный элемент случайности.