3. Сформулируйте, при каких обстоятельствах достигает функция максимума, минимума, при каких обстоятельствах остается вопрос открытым и требуются дополнительные исследования.

4. В чем экономический смысл уравнения связи? Как она выбирается?

5. При каких обстоятельствах используется метод неопределенных множителей Лагранжа?

6. В чем экономический смысл метода наименьших квадратов?

7. Каким образом определяются параметры системы? Например, а, b, c для функции

у = .

8. В чем экономический смысл величины ε₁, ε₂, …, ε_n в системе МНК? Всегда ли они имеют место?

9. Сформулируйте правило составления системы стандартных уравнений.

10. Составьте систему стандартных уравнений для следующих функций:

1. у = а - bx; 2. y = ;

3. y = a + bx + c ; 4. y = ;

5. y = ; 6. y = a · b^x;

7. y = a · x^b; 8. y = a + a₁x₁ + a₂x₂.

11. Прокомментируйте наиболее привлекательные функции для исследования спроса, предложения, выпуска продукции.

12. Дайте оценку функции у = ℓоg х для исследования спроса, выпуска продукции.

13. Сформулируйте общую схему исследования функции и построения их графиков.

1.10. Тренировочные задачи

1. Исследовать на максимум и на минимум функции:

1. ; 2. ;

3. ; 4. ;

5. .

2. Исследовать на возрастание и убывание следующие функции:

1. ; 2.;

3. у = е^кх; 4. ;

5. .

3. Исследовать на экстремум следующие функции:

1. ; 2.;

3. ; 4.;

5. ; 6.у = х² е^-х;

7. ; 8..

4. Найти наибольшее, наименьшее значения функций:

1.на отрезке [-4; 4];

2. на отрезке [1,е];

3..

5. Найти асимптоты кривых:

1. ; 2.;

3. ; 4.;

5. ; 6..

6. Исследовать функции и построить их графики:

1. ; 2.;

3. ; 4.;

5. ; 6..

1.11. Тест к разделу 1

1. Выберите неравенство, при котором функция достигает экстремума:

а) АС - В² > 0;

б) АС - В² < 0;

в) АС - В² = 0;

2. Отметьте необходимые условия существования экстремума функции:

а) > 0,> 0;

б) < 0,< 0;

в) = 0,= 0.

3. Укажите вспомогательную функцию Лагранжа:

а) Z = ƒ [x1 + (x)] = F(x);

б) Ф(х₁у) = ƒ(х₁у) + λφ(х₁у);

в) Ф(х₁у) = х +у + λ.

4. Укажите, правильно ли составлены системы стандартных уравнений:

а)

для функции у = а + bt;

б)

для функции ;

в)

для функции у = а + а₁х₁ + а₂х₂ .

5. Выберите привлекательные функции для прогнозирования:

а) у = а + bt;

б) у = аb^t;

в) .

Раздел 2. Эконометрические модели

Теперь непосредственно рассматриваем эконометрические модели отдельных экономических показателей, составляющих. Например, эконометрические модели спроса, ценообразования, равновесия и другие. Эти модели, как правило, исследуются на основе выше приведенной системы математического аппарата. Рекомендации, обоснованные на основе эконометрических моделей, могут носить как локальный, так и глобальный характер. Очень многое зависит от масштаба экономической постановки задач.

Цель раздела: закрепление теоретических знаний с практических позиций.

2.1. Измеряющие (регрессионные) модели и корреляция

Простейшим видом измеряющих (регрессионных) моделей являются модели, характеризующие зависимость между двумя признаками (факторами), т.е. модели вида:

y = ƒ (x),

где y - зависимая переменная, т.е. результативный признак;

x - независимая или объясняющая переменная величина, т.е. признак фактора.

Например, бизнесменов, предпринимателей, экономистов, менеджеров интересует как изменится спрос на конкретный вид товара, если цены увеличатся на 12,3%, причем, при насыщенности рынка на данный товар на уровне 84,5%. Или в какой степени является целесообразным увеличение выпуска продукции на 15,5%, если цены на товары увеличиваются на 8,4%, а насыщенность рынка составляет не более 92%. Или еще, их интересует: какие товары надо производить, какого качества, в каком количестве, на какой рынок следует ориентироваться и т.д.

На все эти вопросы отвечают измеряющие эконометрические модели, если они подобраны, обоснованы адекватно, повторяю, если они выявлены с учетом объективной, достоверной информацией, а также учета комплекса внутренних и внешних факторов. В связи с этим хотелось бы, чтобы слушатели внимательно относились к эконометрическим моделям, исследованиям.

При количественной оценке связей между двумя переменными возможны использования следующих функций:

1. у = а + bx; 6. y = a · b^x;

2. y = а +;7. y = ;

3. y = a · x^b; 8. y = a + bx + cx²;

4. y = ; 9. y = ;

5. y = a + bx + cx²; 10. y = a + bx + cx² + dx³.

Для выяснения адекватности выводов, как правило, вычисляются коэффициенты корреляции и детерминации. Расчеты ведутся по формулам:

,

где r - коэффициент корреляции;

- средняя величина фактора;

- средняя величина результативного признака;

- средняя величина из попарных произведений изучаемых признаков x и y;

- среднее квадратическое отклонение факторного признака;

- среднее квадратическое отклонение результативного признака.

Коэффициент корреляции представляет собой величину, которая колеблется в пределах от 0 до 1.

В тех случаях, когда коэффициент корреляции равен нулю, связь отсутствует. Если же он равен 1, то связь между изучаемыми признаками функциональная, т.е. полная. Знак  коэффициента корреляции указывает на направление связи (плюс - прямая связь, минус - обратная).

Если же r  0,5, связь между факторами можно считать слабой; если 0,51 r  0,8, связь можно рассматривать как среднюю, а если r  0,81 - связь можно отнести к более устойчивой категории.

Линейный коэффициент корреляции можно вычислить и по другим формулам, например:

.

Часто применяется формула, основанная на расчетах отклонений от средней:

.

Коэффициент корреляции имеет ошибку, которая вычисляется по формуле:

.

При этом предполагается, что число наблюдений, по которым ведутся расчеты, является лишь выборкой из большого числа наблюдений "генеральной" совокупности, а вычисленный коэффициент корреляции – только приближенная оценка того "истинного" коэффициента, который характерен для нее.

Для выяснения доли связи между факторами вычисляется коэффициент детерминации:

r² = D.

Измеряется этот коэффициент в процентах.

В случае многофакторной зависимости вычисляется коэффициент множественной корреляции:

.

Квадратическая ошибка коэффициента множественной корреляции исчисляется по формуле:

,

где n – число факторов.

Аналогично определяются и пределы "истинного" коэффициента множественной корреляции в определенных границах с некоторой вероятностью, зависящей от t - доверительного числа:

.

Если мерой тесноты связи при линейной форме служит коэффициент корреляции, то для криволинейной зависимости такую функцию связи выполняет корреляционное отношение, которое вычисляется по формуле:

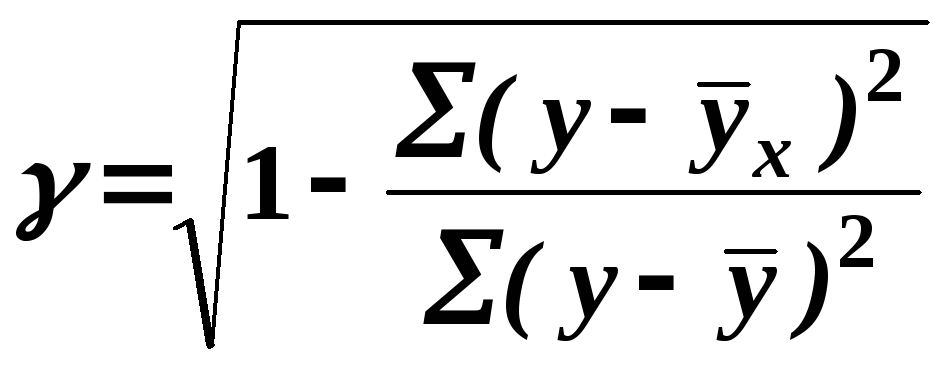, или ,

где у – фактическое значение результативного признака;

- расчетное значение признака;

- среднее значение признака.

Корреляционное отношение как показатель тесноты связи при множественной регрессии используется наравне с коэффициентом множественной корреляции. Корреляционное отношение как мера совокупной связи между признаками имеет вид:

Квадратическая ошибка корреляционного отношения определяется по формуле:

.

Достоверность выводов определяется на основании вычисления: .