1.6.8. Показательная функция

у = а^х, гдеа – положительное число, отличное от единицы. Свойства:

а) показательная функция определена на всей числовой оси;

б) показательная функция положительна при любом значении х, т.е. ее график расположен в верхней полуплоскости;

в) если х = 0, тоу = а⁰= 1, т.е. график функции пересекает ось ординат в точке (0, 1);

г) если а> 0, тоу = а^х> 1 при положительных значенияххиу = а^х< 1 при отрицательных значенияхх;

д) если а> 1, то функция возрастает;

е) если 0 ≤ а≤ 1, тоу = а^х< 1 при положительных значенияххиу = ах> 1 при отрицательных значенияхх;

ж) если 0 < а< 1, то показательная функция убывает.

Перечисленные свойства видны из графика (рис. 21).

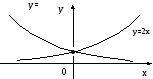
Рис. 21

Легко убедиться в том, что графики функций а^хисимметричны относительно оси ординат.

График функции .Чтобы построить график функции ,надо построить график функцииу = а^х, а затем произвести растяжение в (р) раз вдоль оси абсцисс. Поскольку

,

то можно сразу построить график функции с основанием .Это значит, что растяжение показательной функциив (р) раз вдоль оси абсцисс равно сильно переходу от графика показательной функции с основаниемак графику показательной функции с основанием.

График функции у = а^х-с. Чтобы построить график функции

у = а^х-с,

где с– постоянная величина, надо сначала построить график функции у = а^х, а затем произвести перемещение вдоль оси абсцисс на отрезок, равныйс. Но так как

,

то можно построить сначала график функции у = а^х, а затем произвести растяжение этого графика вдоль оси ординат враз.

Таким образом, перемещение графика функции у = а^хвдоль оси абсцисс на отрезок (с) равносильно его растяжению вдоль оси ординат враз.

График функции у = а^х ∙ b^x. Построим произведение графиков функций ,. Имеем

у = у₁ ∙ у₂ = а^xb^x = (аb)^x.

Таким образом, чтобы построить произведение графиков показательных функций с различными основаниями, достаточно построить график функции при основании, равном произведению их оснований.

1.6.9. Логарифмическая функция

Функция, определяемая равенством

,

где а– положительное, отличное от единицы число, называется логарифмической функций. По существу логарифмическая функция обратна показательной, поэтому график ее симметричен графику показательной функции относительно биссектрисы первого и третьего координатных углов.

На рис. 22 показаны графики функции (пунктирная линия) и(сплошная линия), а на рис. 23 графики функцийи.

Свойства логарифмической функции легко можно усмотреть из рис. 21 и 22.

Логарифмическая функция определена только для положительных чисел (0 < x< +∞), т.е. график расположен правее оси ординат.

Если а> 1, то логарифмическая функции положительна прих> 1, отрицательная при 0 <х< 1 и равна нулю прих= 1.

Рис. 22 Рис. 23

При а> 1 логарифмическая функция возрастает. Если 0 <а< 1, то она положительна при 0 <х< 1, отрицательна при х > 1, равна нулю при х = 1.

Если 0 < а< 1, то функция является убывающей, еслиа> 1 график функции выпуклый; если 0 <а < 1 . то график логарифмической функции вогнут.

На рис. 24,25 представлены привлекательные функции для исследования (оценки) поведения различных технико-экономических показателей, в частности спроса и предложения.

Рис. 24

Рис. 25