Тема 7 Исследование системы двух случайных величин
Функция
распределения вероятностей системы
двух случайных величин. Вероятность
попадания значений двумерной случайной
величины (
,
)
в прямоугольник со сторонами, параллельными
координатным осям.
Плотность вероятности. Условная плотность распределения. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции. Уравнение линейной регрессии.
Практическое занятие включает:
-
определение вероятности попадания
значений двумерной случайной величины
(
,
)
в прямоугольную область со сторонами,
параллельными координатным осям;
-
определение законов распределения
составляющих
и
по заданному распределению вероятностей
дискретной двумерной СВ;
- нахождение функции распределения, двумерной и условной плотностей распределения системы двух СВ;
- определение МО и дисперсии составляющих, а также корреляционного момента системы двух СВ.
Вопросы
Что называется системой двух случайных величин (
,
)?Дайте определение функции распределения вероятностей системы двух случайных величин
и перечислите ее свойства.Как с помощью функции распределения
определяется вероятность попадания
двумерной случайной величины (
,
)
в прямоугольник
,
?Дайте определение двумерной плотности вероятности
и перечислите ее свойства.Как, зная
,
определить функцию распределения
и вероятность попадания случайной
точки (
,
)
в область
.Поясните суть вероятностной зависимости между случайными величинами
и
.
В чем ее отличие от функциональной
зависимости?Что называется условным законом распределения случайной величины
,
входящей в систему (
,
)?Запишите соотношение, выражающее условную плотность распределения составляющей
при заданном значении
через плотность совместного распределения
системы (
,
)
и плотность распределения составляющей
.О чем говорит равенство условных плотностей распределения случайных величин
и
их безусловным плотностям?Как называется отклонение случайной величины
от
ее математического ожидания?Дайте определение начального момента порядка k,s системы (
,
).Дайте определение центрального момента порядка k,s системы (
,
).Приведите формулы для определения математических ожиданий и дисперсий непрерывных случайных величин
,
,
составляющих систему (
,
).Запишите формулу корреляционного момента
системы случайных величин (
,
).
Что он характеризует?Чем обусловлено введение в рассмотрение в качестве характеристики связи между случайными величинами
и
коэффициента корреляции?Какую зависимость между случайными величинами
и
характеризует коэффициент корреляции?Какая связь существует между равенством нулю коэффициента корреляции и независимостью случайных величин
и
?В каком случае две случайные величины
и
называются коррелированными
(некоррелированными)?Приведите формулу для определения корреляционного момента непрерывных случайных величин
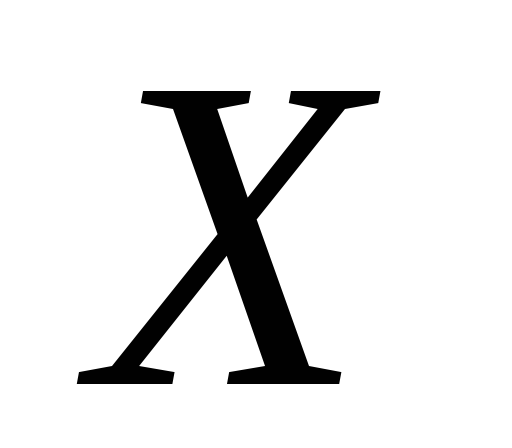и
.Запишите формулы для определения числовых характеристик системы двух дискретных случайных величин
и
:
,
,
,
,
.Запишите уравнение линейной регрессии
от
и объясните смысл входящих в него
величин.что называется линией регрессии
от
?