Тема 2 Случайные величины и законы их распределения. Закон распределения вероятностей и числовые характеристики дискретной случайной величины. Повторение испытаний

Числовые характеристики дискретной случайной величины (СВ). Свойства математического ожидания (МО) и дисперсии. Ряд распределения как простейшая форма закона распределения дискретной СВ. Математическое ожидание и дисперсия числа появлений события в независимых испытаниях. Повторение испытаний. Формула Бернулли (биномиальное распределение). Формула Пуассона как асимптотическое приближение формулы Бернулли. Геометрическое распределение.

Практическое занятие включает:

- определение числовых характеристик дискретной СВ, заданной рядом распределения;

- рассмотрение свойств математического ожидания и дисперсии;

- решение примеров на использование формул Бернулли и Пуассона;

- рассмотрение примеров геометрического распределения случайной величины.

Вопросы

1. Понятие случайной величины. Дискретные и непрерывные случайные величины.

2. Что устанавливает закон распределения случайной величины?

3. В каком виде обычно задается закон распределения дискретной случайной величины?

4. Как определяются математическое ожидание М(Х), дисперсия D(X) и среднее квадратическое отклонение б (Х) дискретной случайной величины Х, принимающей конечное множество значений?

5. Изложите свойства математического ожидания и дисперсии случайной величины.

6. Какими должны быть испытания, чтобы можно было применить формулу Бернулли (биномиальное распределение)?

7. Изложите условия, при которых можно применять закон распределения Пуассона. Почему этот закон называют законом редких явлений?

8. Дайте характеристику схемы испытаний, приводящей к геометрическому распределению дискретной случайной величины.

Примеры

Пример 1. Монета подбрасывается 4 раза. Случайная величина Х– «число выпадения герба при этих подбрасываниях». Найти числовые характеристики СВ Х: М(Х), D(Х), б(Х).

Решение. Данная дискретная СВ Х может принимать 5 значений: ,,,,. Закон распределения СВХ можно задать таблицей.

Х	0	1	2	3	4
Р

Математическое ожидание

.

Закон распределения СВ имеет вид

	0	1	4	9	16
Р

Математическое ожидание

.

По формуле для дисперсии получаем

.

Среднее квадратическое отклонение (СКО)

.

Пример 2. Дискретная случайная величина , которая может принимать бесконечную последовательность значений,задана следующим законом распределения

				…		…
Р				…		…

.

Найти МО случайной величины .

Решение. По формуле математического ожидания дискретной случайной величины находим.

.

Пример 3. Производятся независимые опыты, в каждом из которых событие А наступает с вероятностью р. Опыты повторяются до первого появления события А. Случайная величина - число произведенных опытов. Найти математическое ожидание случайной величины.

Решение. Возможные значения этой случайной величины: ,. Событиеозначает, что в первыхопытах событиеА не наступает, а в -м опыте наступает. Вероятность такого исхода равна

, ().

Следовательно, закон распределения СВ Х можно представить таблицей

х	1	2	3	…		…
р				…		…

Математическое ожидание этой величины

Ряд в скобках получается почленным дифференцированием ряда геометрической прогрессии.

.

Следовательно

.

Пример 4. Установлено, что из каждых 100 деталей не имеют дефектов 75 штук в среднем. Составить закон распределения числа пригодных деталей из взятых на удачу 6 деталей.

Решение. Из условия задачи следует, что ,,. В соответствии с формулой Бернулли.

, где , находим

;

;

;

;

.

Закон распределения данной случайной величины - «числа стандартных деталей из 6 взятых наудачу» имеет вид:

	0	1	2	3	4	5	6
	0,000	0,004	0,033	0,132	0,297	0,356	0,178

Контроль: .

Полигон полученного биномиального распределения представлен на рис.

Пример 5. Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года равна 0,001и не зависит от состояния других элементов. Какова вероятность отказа: двух элементов; не менее двух элементов в год?

Решение. Здесь требуется найти вероятности: и. По условию,,.

Вероятность отказа ровно двух элементов найдем по формуле Пуассона

=> .

Вероятность отказа не менее двух элементов:

.

Пример 6. Доказать, что распределение Пуассона является предельным случаем биномиального распределения.

Решение. Из формулы определяеми:,и подставим в формулу Бернулли:

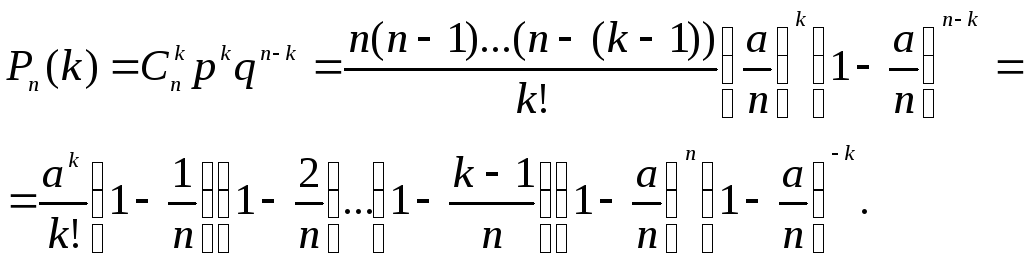
Переходя к пределу при , получим

,

что и требовалось доказать.

Пример 7. Производится подбрасывание игрального кубика до первого выпадения шести очков. Какова вероятность того, что первое выпадение шестерки произойдет при втором подбрасывании игрального кубика?

Решение. Воспользуемся формулой геометрического распределения дискретной случайной величины .

, .

В данном случае (вероятность появления шестерки при подбрасывании кубика) и, то

.

Задачи

1. Закон распределения дискретной случайной величины задан таблицей

	-2	-1	0	1	2
	0,1	0,2	0,4	0,2	0,1

Найти .

2. Подбрасываются два игральных кубика. Дискретная случайная величина - сумма очков, выпавших на обоих кубиках. Найти закон распределения и математическое ожидание случайной величины.

3. Задают ли данные таблицы законы распределения дискретной случайной величины?

а)					…		…
	Р				…		…

б)					…		…
	Р	1			…		…

4. Случайная величина распределена по закону Пуассона с параметром. Найти МО и дисперсию величины.

5. Вероятность появления события А в испытании равна 0,1. Найти СКО числа появлений события А в одном испытании.

6. Производятся независимые испытания, в каждом из которых событие А может появиться с вероятностью . Найти вероятность того, что при 2000 испытаниях событиеА появится 3 раза.

7. Известно, что в принятой для сборки партии из 1000 деталей имеются 4 дефектных. Найти вероятность того, что среди 50 наугад взятых деталей нет дефектных.

8. Завод отправил на базу 5000 качественных изделий. Вероятность повреждения изделия в пути равна 0,0002. Найти вероятность того, что в пути будет повреждено:

а) ровно 3 изделия; б) ровно одно изделие;

в) не более 3 изделий; г) более 3 изделий.

9. Найти вероятность того, что при бросании игрального кубика первое появление шестерки произойдет при втором бросании.