1.6. Перечисление классов эквивалентности. Лемма Бернсайда и теорема Пойа.

Рассмотрим задачу о числе раскрасок граней куба в 3 цвета: белый (white), синий (blue) и красный (red). Так как есть три возможности для раскраски каждой из 6 граней, то всего раскрасок 3⁶=729. Далее, можно найти число раскрасок, использующих i раз белый, j раз синий и k раз красный цвет (i+j+k=6). Для этого достаточно раскрыть с помощью полиномиальной формулы

.

При этом фактически каждой грани куба ставится в соответствие скобка , и выбор цвета при раскраске грани соответствует выбору буквы при раскрытии скобок. Таким образом, раскрасок, использующихi раз белый, j раз синий и k раз красный цвет, имеется

.

Эти формулы, однако, справедливы лишь в том случае, если все грани куба различны, другими словами, куб занимает определенное положение в пространстве. Если же куб можно поворачивать, самосовмещая его, то различные раскраски могут переходить друг в друга, совмещаться. При этом естественно считать совместимые раскраски одинаковыми и ставить задачу нахождения числа различных раскрасок. На математическом языке это можно выразить следующим образом. Группа самосовмещающих вращений куба действует как группа перестановок на множестве из 3ⁿ раскрашенных кубов. Совместимость различных раскрасок является отношением эквивалентности. Классы эквивалентности принято называть в данном случае орбитами. Таким образом, требуется найти число орбит, а также число орбит, раскраски которых используют заданное число раз каждый из цветов.

Сформулируем общий результат о числе орбит, возникающих при действии группы на конечном множестве, выражаемый классической леммой Бернсайда*. Пусть группа G действует на конечном множестве Х, элементы которого будем называть точками. Результат действия элемента группы на точкубудем обозначать через, т.е. писать точку в скобках слева от действующего на нее элемента группы с тем, чтобы сохранить порядок действий слева направо. Точкуназовем стационарной для элемента, если. ЧерезX_g обозначим множество стационарных для точек.и- число элементов множестваи группы.

Лемма Бернсайда. Число орбит N при действии группы G на конечном множестве точек X равно среднему по группе числу стационарных точек

.

Прежде чем дать доказательство, проиллюстрируем лемму примерами. Пусть циклическая группа подстановок шестого порядка, порожденная подстановкой , действует на множестве символов. Циклыии будут в данном случае орбитами действия группы. Выпишем перестановки группы:

;

;

;

;

;

.

Просуммировав число стационарных точек по всем перестановкам и разделив полученную сумму на порядок группы, получаем (5+0+2+3+2+0)/6=2, в полном соответствии с леммой.

Рассмотрим теперь пример, более близкий к нашей задаче о раскраске граней куба. Пусть вершины квадрата раскрашиваются двумя цветами: красным (red) и синим (blue). Всего таких раскрасок 2⁴=16. Квадрат может поворачиваться относительно центра на углы 0⁰, 90⁰, 180⁰, 270⁰, самосовмещаясь. При этом одна раскраска может переходить в другую. Требуется найти число различных раскрасок с учетом самосовмещений, т.е. число орбит действия группы поворотов на множестве 16 раскрашенных квадратов. Выпишем эти раскраски, обозначив ихx₁x₁₆:

*Бернсайд Уильям (1852-1927) английский математик, внесший значительный вклад в развитие теории групп конечного порядка.

Группа поворотов имеет порядок 4 и является циклической. Она порождается поворотом на 90⁰по часовой стрелке, который обозначим как. Тогда. Выпишем действие элементов группы на множестве 16 раскрасок:

;

;

;

.

Подсчитав число стационарных точек и применив формулу Бернсайда для определения числа орбит, получим (16+2+4+2)/4=6. Эти 6 орбит снова являются циклами порождающего элемента :,,,,,.

Может показаться, что непосредственное выписывание орбит позволяет найти их число быстрее, чем определение их числа с помощью подсчета числа стационарных точек и применении леммы Бернсайда. Однако легкость выписывания орбит в данном случае, с одной стороны, объясняется цикличностью группы , а с другой стороны, это действие обозримо вследствие сравнительно небольшого числа раскрашенных квадратов, на которых действует группавсего 16. На множестве 729 раскрашенных кубов подобные действия, задаваемые вращениями, выписать в явном виде было бы значительно труднее. В то же время, нахождение числа стационарных раскрасок можно осуществить значительно проще, если рассмотреть действие группыне на множестве 16 раскрашенных квадратов, на множестве вершин квадрата, которых всего 4:

;

;

;

,

и заметить, что некоторая раскраска является стационарной для данной перестановки в том и только в том случае, если все вершины каждого цикла перестановки выкрашены одним цветом. Таким образом, перестановка, состоящая из циклов, имеетстационарных раскрасок, гдечисло цветов (в нашем случае).

Сделанное замечание вместе с леммой Бернсайда позволяют найти число орбит как (2⁴+2¹+2²+2¹)/4=6. Это вычисление может быть представлено в изящной форме, если ввестицикловой индекс группыGна множестве вершин квадрата. Цикл длиныбудем обозначать переменной, а каждую перестановку представим как произведение входящих в нее циклов: ,,,. Просуммировав соответствующие перестановкам мономы и поделив полученный полином на порядок группы, получим цикловой индекс группыGот переменных:

.

Теперь для нахождений числа раскрасок достаточно подставить в цикловой индекс вместо каждой из переменных число используемых цветов: .

Цикловой индекс позволяет также получить число раскрасок, использующих фиксированное число раз каждый из цветов. Для этого достаточно вместо переменной каждой из переменных циклового индекса подставить выражениеи привести полином к стандартному виду суммы произведений:

.

Теперь коэффициент при мономе показывает число раскрасок, использующихраз голубой ираз красный цвет. Таким образом, имеется по одной одноцветной раскраске, по одной раскраске, использующей один раз один цвет и три раза другой, и две раскраски, использующие каждый из цветов дважды. Это можно и непосредственно увидеть, рассмотрев представленные выше 6 орбит на множестве раскрасок. Получение числа раскрасок с фиксированным числом использования каждого из цветов относится к более продвинутой теории, использующей теорему Пойа, которая будет рассмотрена после доказательства леммы Бернсайда.

Доказательство. Пусть - одна из орбит при действииG на X. Пусть A_i – множество элементов таких, что,. Тогдагде- стабилизатор точки, т.е. такая подгруппа группыG, элементы которой оставляют на месте точку , а– произвольный фиксированный элемент множества. В самом деле, ясно что, так как. Докажем обратное включение. Пусть, т.е.. Тогда, так как. Поэтому. Этим доказывается, что, т.е.. Таким образом,, множество смежных классов по стабилизатору . По теореме Лагранжа

;

;

Такую же мощность имеют и стабилизаторы остальных точек орбиты

, .

Поэтому .

Рассмотрим теперь двудольный граф, одну долю которого составляют элементы группы G, другую – точки множества X. Ребро проводится в том и только в том случае, если точкаявляется стационарной для элемента.

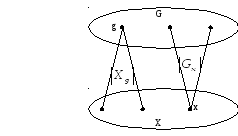
Подсчитаем теперь число ребер графа двумя способами: с верхней доли и с нижней доли. С верхней доли подсчет дает

.

С нижней доли подсчет дает

.

Если последнюю сумму разбить по орбитам, то вклад каждой орбиты по доказанному ранее будет равен . Поэтому вся сумма будет равна, где число орбит. Имеем

.

Откуда

.

Лемма доказана.

Вернемся теперь к задаче о раскраске граней куба. С этой целью рассмотрим группу самосовмещающих вращений куба. Так как куб можно поставить на стол любой из 6 своих граней и при этом имеется ещё 4 самосовместимых положения, то эта группа содержит элемента, а именно:

1. Тождественное вращение.

2. 3 нетождественных вращения вокруг каждой из 3 осей, соединяющих середины противоположных граней,  итого 9 вращений.

3. 2 нетождественных вращения вокруг каждой из 4 осей, соединяющих противоположные вершины,  итого 8 вращений.

4. 1 нетождественное вращение вокруг каждой из 6 осей, соединяющих середины противоположных ребер,  итого 6 вращений.

Выпишем циклическую структуру каждого из вращений как перестановки на множестве 6 граней.

1. Тождественное вращение оставляет каждую из 6 граней на месте. Запишем это как 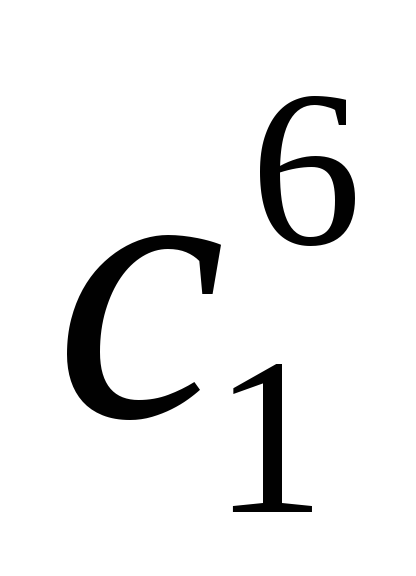(6 циклов длины 1).

2. Эти вращения по циклической структуре разбиваются на 2 класса: вращения на 180⁰ и вращения на 90⁰. Первые имеют циклическую структуру (2 цикла длина 1 и 2 цикла длины 2), вторые -(2 цикла длины 1 и 1 цикл длины 4).

3. Эти вращения имеют циклическую структуру (2 цикла длины 3).

4. Это вращение имеет циклическую структуру (3 цикла длины 2).

Просуммировав циклические структуры всех перестановок и поделив сумму на число элементов в группе, получим цикловой индекс группы

.

Рецепт для нахождения числа раскрасок остается прежним. Достаточно в цикловой индекс вместо каждой из переменных подставить число используемых красок в данном случае 3:

.

В самом деле, как и прежде, для данной перестановки граней куба раскраска будет стационарной в том и только в том случае, если грани, принадлежащие одному циклу, выкрашены в одинаковый цвет. Поэтому, если циклическая структура перестановкиестьи используются 3 цвета, то она имеетстационарных раскрасок и рецепт является прямым следствием леммы Бернсайда.

Для того, чтобы найти число раскрасок, использующих раз белый,раз синий ираз красный цвет, нужно в цикловой индекс вместо каждой переменнойподставить выражениеи, раскрыв скобки в выражении

, найти коэффициент при . Этот рецепт составляет содержание теоремы Пойа^*. Обоснуем его.

^*Пойа Дьердь (1887-1985)  венгерский математик, работавший в различных разделах математики, автор известных книг по математике и преподаванию математики.

Будем рассматривать действие группы вращений лишь на раскрасках типа и подсчитаем число орбит на этом множестве. Лемма Бернсайда дает:

,

где множество раскрасок типа , не изменяющихся при вращении. Теперь для обоснования рецепта Пойа остается лишь заметить, что для подсчета числа стационарных раскрасок у вращения с циклической структурой нужно вместо каждой переменнойподставить выражениеи, раскрыв скобки, найти коэффициент при мономе. Это следует из того, что для стационарности раскраски необходимо и достаточно, чтобы все грани цикла были выкрашены одним цветом, т.е. каждый цикл длиныдаетграней одного из цветов, и выбор переменной при раскрытии скобкив процессе перемножения скобок соответствует выбору цвета при раскраскеграней цикла.

В качестве примера найдем число раскрасок, использующих каждый цвет дважды. Коэффициент, получающийся при после раскрытия скобок в выражении

равен

,

что и дает число искомых раскрасок.

В качестве еще одного примера на применение теоремы Пойа рассмотрим следующую задачу. Сколько различных ожерелий из 7 бусинок можно составить, используя 3 красных и 4 синих бусинки?

Ожерелья, получающиеся передвижением бусинок по нитке ожерелья, а также переворотом ожерелья, считаются одинаковыми. Поэтому с математической точки зрения задача эквивалентна числу раскрасок вершин правильного 7-угольника, использующих 3 раза красный цвет и 4 раза синий.

Группа самосовмещений 7-угольника состоит из 7 поворотов на углы 0⁰, 360⁰/7, 2360⁰/7, 3360⁰/7, 4360⁰/7, 5360⁰/7, 6360⁰/7 и 7 переворотов относительно прямых, соединяющих вершины с серединами противоположных сторон:

Поворот на нулевой угол как тождественное преобразование имеет циклическую структуру , а все остальные повороты при действии на множестве вершин состоят из одного цикла, т.е. их циклическая структура. Каждый переворот оставляет одну из вершин на месте, а остальные 6 разбивает на циклы длины 2, т.е. имеет циклическую структуру. Поэтому цикловой индекс группы самосовмещений 7-угольника есть

.

Теперь для нахождения числа раскрасок, использующих 3 раза красный цвет и 4 раза синий, нужно, согласно рецепту Пойа, раскрыв выражение

,

найти коэффициент при . Этот коэффициент, как нетрудно заметить, равен

.

Таким образом, существует 4 ожерелья заданного типа. Вот они:

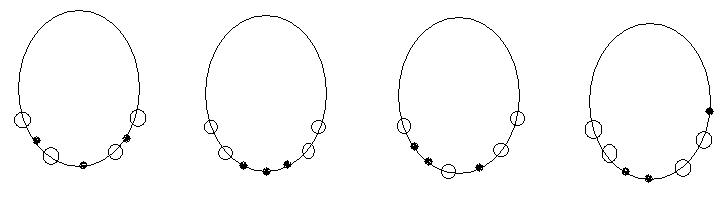
Вопросы для самопроверки.

1. Цикловой индекс группы самосовмещающих вращений куба, действующей на множестве его вершин, равен

а) ; б); в).

2. Число различных раскрасок вершин куба в 2 цвета с учетом самосовмещений равно а) 21; б) 22; в) 23.

3. Число различных раскрасок вершин куба в 2 цвета, использующих 3 раза красный и 5 раз синий цвет, с учетом самосовмещений равно а) 2; б) 3; в) 4.