Глава II. Булевы функции.

2.1. Определение и интерпретация.

Если каждому элементу множества поставлен в соответствие единственный элемент множества, то говорят, что задано отображение извили функция. Ощепринятой записью функции является также обозначение

, где ,. Если в математическом анализе в качестве множестви, выступают, как правило, множество действительных чисел или его интервалы, то в дискретной математике рассматриваются функции, область определения и множество значений которых являются конечными множествами. Особенно важными являютсябулевы функции, отображающие некоторую декартову степень множества в множество, названные так в честь Джорджа Буля (1815-1864) английского математика-самоучки, заложившего основы математической логики. Ввиду значения булевых функций в математической логике их часто называют также функциями алгебры логики. Помимо математической логики, булевы функции нашли применение при проектировании и описании функционирования дискретных кибернетических устройств, в частности, компьютеров.

Булевой функцией от переменныхназывается функция, определенная на множестве всех двоичных наборов длиныи принимающая на каждом из них значениеили.

Так как имеется двоичных наборов длины, то булевых функций отпеременных. Множество булевых функций отпеременных обозначается, а объединениеобозначается. При этом под функциями, зависящими от нулевого числа переменных, понимаются константыи. Множествосчетно.

Булева функция может быть задана таблично, т.е. для каждого из наборов значений переменных, выписанных в лексикографическом порядке (по возрастанию двоичных чисел), выписывается значение функции на этом наборе. Такую таблицу принято называтьтаблицей истинности.

При имеем 4 булевы функции, которые могут быть заданы таблично как

При этом функция называетсятождественной, а функция  отрицанием (читается «не»). Заметим, что

.

Помещенные в таблицу как булевы функции от одной переменной 0 и 1 в действительности являются константами и не зависят от переменной . Переменнаяявляется в данном случае фиктивной или, как говорят, несущественной переменной. В общем случае переменнаяфункцииназываетсясущественной, если для некоторых

.

В противном случае она называется фиктивной или несущественной переменной. Заметим, что в включаются и функции, зависящие фактически от меньшего числа переменных, поскольку некоторые переменные у функции могут быть несущественными. Отождествив между собой функции, получающиеся одна из другой изъятием или добавлением несущественных переменных, имеем, при.

Булевых функций от двух переменных имеется уже 16. При этом наибольшее значение и специальные названия имеют семь из них:

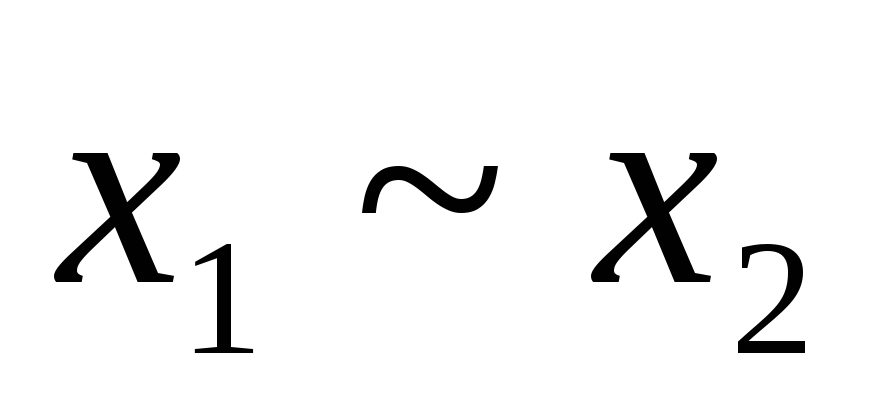
1

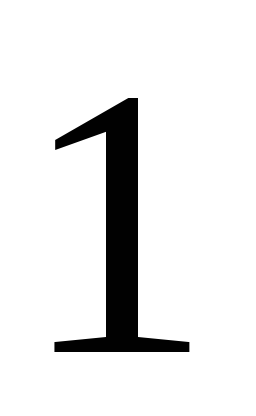
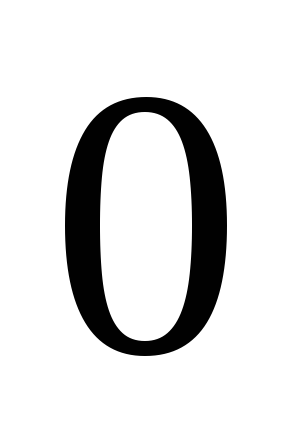
 конъюнкция (связка «и», логическое умножение), обозначается также , или просто ;

 дизъюнкция (связка «или»-неразделительное, логическое сложение);

 импликация (логическое следование);

эквивалентность;

 сложение по модулю 2 (связка «или»-разделительное);

штрих Шеффера;

стрелка Пирса.

Дизъюнкция, конъюнкция, импликация, эквивалентность и сложение модулю 2 используются в качестве логических связок в логике высказываний и являются эквивалентами союзов и языковых конструкций «и», «или», «если … , то», «в том и только в том случае, если», «либо … , либо». При этом значению высказывания «истина» соответствует значение булевой переменной 1, а значению «ложь»  0. Пусть обозначает высказывание «я пойду гулять», а«я буду заниматься математикой». Тогда следующие булевы выражения будут обозначать высказывания:

 «я пойду гулять или буду заниматься математикой» (причем

допускается, что я буду делать и то, и другое, хотя в естественном

языке союз «или» может использоваться как в разделительном, так и

в неразделительном смысле, что оставляет некоторую

неопределенность);

 «я или пойду гулять, или буду заниматься математикой» (здесь

возможность и того, и другого уже исключается);

 «я пойду гулять и буду заниматься математикой» (очевидно, на

прогулке);

 «если я не пойду гулять, то буду заниматься математикой» (если в

естественном языке подобная фраза часто подразумевает, что

прогулка исключает занятие математикой, то при записи

высказывания формулой занятие математикой допускается и в случае

прогулки);

«я буду заниматься математикой в том и только в том случае, если я не

пойду гулять».

Приведенные примеры наглядно демонстрируют точность составных высказываний, образованных из простых с помощью булевых операций, на фоне двусмысленности естественного языка.

Так как область изменения каждой переменной булевой функции есть множество , а множество её значений также принадлежит этому множеству, то это позволяет вместо каждой из переменных некоторой булевой функции подставлять другие функции, получая, таким образом, из имеющегося запаса функций новые функции и выражая одни функции через другие. Такая подстановка в математике называетсякомпозицией или суперпозицией функций. В теории булевых функций эта операция занимает особенно важное место.

Так, импликация и эквивалентность могут быть выражены через дизъюнкцию, конъюнкцию и отрицание:

;

,

что может быть проверено непосредственно с помощью таблиц истинности перебором всех возможных значений и. При этом запись второй формулы использует общепринятое соглашение, согласно которому конъюнкция выполняется раньше, чем дизъюнкция и сложение по модулю 2, что позволяет опустить часть скобок.

Кроме того, эквивалентность может быть выражена через импликацию

,

что вполне отвечает привычному представлению о том, что эквивалентно, есливлечетивлечет.

Сложение по модулю 2 выражается через дизъюнкцию, конъюнкцию и отрицание как

.

Штрих Шеффера, стрелка Пирса также выражаются через дизъюнкцию, конъюнкцию и отрицание:

;

.

Для дизъюнкции, конъюнкции и отрицания справедливы следующие соотношения:

;

;

;

;

;

;

;

,

а также правила де Моргана:

;

.

Для дизъюнкции, конъюнкции, эквивалентности и сложения по модулю 2 имеют место также следующие алгебраические свойства.

1. Коммутативность (переместительный закон):

;

;

;

.

2. Ассоциативность (сочетательный закон):

;

;

.

3. Дистрибутивность (распределительный закон):

;

;

.

В процессе преобразования булевых выражений, содержащих дизъюнкцию, конъюнкцию и отрицание, особенно часто используются формулы

(поглощение);

(слияние),

где и произвольные булевы функции. Слияние особенно часто используется в форме

(склеивание по переменной ).

Полезна также формула

.

Доказательство этих соотношений легко следует из сформулированных выше основных свойств операций , ,  :

;

;

.

Существует очевидная аналогия между булевыми операциями , ,  и теоретико-множественными операциями объединения, пересечения и дополнения. В самом деле, каждой булевой функции от переменных можно поставить во взаимно однозначное соответствие подмножество тех наборов множества, на которых она принимает значение 1. При этом операциям, ,  над булевыми функциями будут соответствовать операции ,, над соответствующими им множествами. В свете сказанного в справедливости последнего соотношения, например, легко убедиться также с помощью диаграммы Эйлера-Венна:

Так как булевы операции , , , , выражаются, как было показано, через , ,  , то и любая булева функция, выраженная с помощью формулы, использующей лишь эти 8 операций, может быть выражена через , ,  .

В качестве примера рассмотрим формулу . Выразив импликации и эквивалентность через, ,  , имеем

.

Перемножая скобки и помня, что , получаем

.

Удаляя поглощаемые члены, завершаем преобразование

.

Подобные булевы выражения, состоящие из конъюнкций переменных и их отрицаний, соединенных функциональными символами дизъюнкции, называются дизъюнктивными нормальными формами (д.н.ф.). Они являются основным средством представления булевых функций в математической логике. Далее будет показано, что любая булева функция может быть выражена с помощью д.н.ф..

Получив в данном примере в результате тождественных преобразований формулу, в которое не входит переменная , можно сделать вывод, чтоявляется фиктивной переменной и в исходном булевом выражении.

Полученное в результате преобразований булево выражение можно представить и в другом стандартном виде. Воспользовавшись законом дистрибутивности, имеем

.

Полученное булево выражение, состоящее из дизъюнкций переменных и их отрицаний, соединеннх функциональными символами конъюнкций, называется конъюнктивной нормальной формой (к.н.ф.). Подобно д.н.ф., к.н.ф. также является унивесальным способом представления булевых функций. Простейшим же представлением в данном случае будет, очевидно, формула .

Если взглянуть на те приведенные выше основные соотношения для булевых функций, куда входят только операции , ,  , то можно заметить, что операции  и , а также константы 0 и 1 входят в них равноправно и симметрично. Точнее, если в каком-либо из соотношений заменить все операции  на , а все операции  на , одновременно заменив 1 на 0 и 0 на 1, то снова получится одно из выписанных соотношений (другое или то же самое). Например, друг в друга переходят правила де Моргана, а также законы дистрибутивности. Подобная симметрия операций  и  не является случайностью и находит объяснение в принципе двойственности.

Если в булевой алгебре константы 1 и 0 поменять местами, т.е. заменить 0 на 1 и 1 на 0, то функция перейдет в функцию (заменяются на противоположные как значения переменных, так и значение функции).

Определение 1. Функция называется двойственной к функции .

Утверждение 1. Соотношение двойственности является взаимным:

.

Доказательство. .

Утверждение 2. Дизъюнкция и конъюнкция двойственны друг другу:

.

Доказательство: .

Определение 2. Функция называется самодвойственной, если

.

В качестве примеров самодвойственных функций можно указать ,,и т.д..

Утверждение 3. Имеется самодвойственных булевых функций отпеременных.

Доказательство. На любом наборе из каждой пары двух взаимно противоположных наборов исамодвойственную функцию можно задать произвольно. Тогда на другом наборе пары функция однозначно определится, приняв противоположное значение. Так как имеется пар наборов, то число самодвойственных функций равно .

Утверждение 4. Пусть и  тождественно равные булевы выражения. Тогда и также тождественно равны.

Доказательство следует из цепочки импликаций

Лемма 1. Функция, двойственная к суперпозиции булевых функций, есть суперпозиция двойственных функций:

.

Доказательство следует из цепочки равенств

Следствие 1. Функция, полученная путем суперпозиции из самодвойственных функций, является самодвойственной.

Теорема 1 (принцип двойственности). Если в некотором булевом тождестве, содержащим лишь операции , ,  , заменить все конъюнкции на дизъюнкции, а дизъюнкции  на конъюнкции, а также заменить 0 на 1 и 1 на 0, то полученное равенство также будет тождеством.

Доказательство. Так как операции  и  взаимно двойственны, то их замена друг на друга приведет в силу леммы 1 к тому, что обе части тождества заменятся соответственно на двойственные функции, которые будут равны в силу утверждения 4.

Булевы функции являются удобным средством для описания функционирования переключательных схем. На это обстоятельство в 1938 году впервые обратил внимание выдающийся американский математик и инженер Клод Шеннон (1916-2001). Пусть схема образована релейными устройствами замыкающего и размыкающего типа. Каждое реле управляется подаваемым на него сигналом. Замыкающее реле разомкнуто при отсутствии сигнала и замыкается при его наличии. Размыкающее реле замкнуто при отсутствии сигнала и размыкается, когда он подается. Замыкающему реле ставится в соответствие переменная , размыкающему , гдепри наличии- го сигнала ипри его отсутствии.

Пусть имеется представленная на рисунке релейная схема.

Последовательное соединение реле описывается, как нетрудно понять, конъюнкцией соответствующих переменных, а параллельное дизъюнкцией. Поэтому проводимость данной схемы описывается булевой формулой, которая после упрощения приводится к виду. Таким образом, схема проводит ток в том и только в том случае, если отсутствует первый сигнал и присутствуют второй и третий.

Вопросы для самопроверки.

1. Сколько существует булевых функций от 3 переменных?

а) 64; б) 256; в) 324.

2. Пусть P обозначает высказывание «будет дождь», а Q  «я пойду гулять».

Как будет выглядеть в этих обозначениях высказывание «если не будет

дождя, то я пойду гулять»?

а) ; б); в).

3. Булево выражение может быть представлено в эквивалентной

форме как

а) ; б)в).