Задачи для самостоятельного решения

1. В буфете имеется 4 ванильных, 2 шоколадных и 3 фруктовых пирожных.

Сколько различных вариантов покупки существует? (Ничего не купить тоже возможный вариант.)

2. Назовем многозначное число симметричным, если оно не изменяет своего значения при чтении в обратном порядке. Сколько существует симметричных 7-значных чисел?

3. За круглым столом с 2nпронумерованными местами нужно рассадитьnмужчин иnженщин так, чтобы никакие два лица одного пола не сидели рядом. Сколькими способами это можно сделать?

4. Сколько диагоналей у правильного 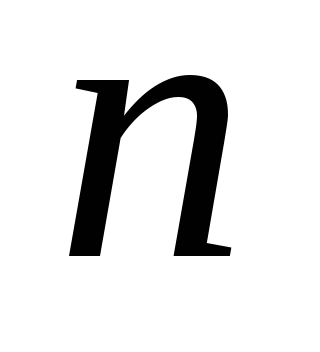-угольника?

5. Прямые на плоскости находятся в общем положении, если каждая пара прямых имеет общую точку, а пересечение каждых трех прямых пусто. Плоскости в простанстве находятся в общем положении, если каждая пара плоскостей пересекается по прямой, каждая тройка плоскостей имеет общую точку, а пересечение каждой четверки плоскостей пусто. Доказать, что

а) прямых общего положения разбивают плоскость наобластей;

б) плоскостей общего положения разбивают пространство наобластей.

6. Найти число бинарных (mn)-матриц,

а) все строки которых различны?

б) не имеющих нулевых строк?

7. Найти число 4^х-значных чисел, у которых каждая последующая цифра не больше предыдущей.

8. Сколькими способами можно разложить mбелых иnчерных шаров в ряд так, чтобы никакие 2 черных шара не лежали рядом? (nm+1)

9. Сколько существует возможных вариантов выпадения при одновременном бросании пяти одинаковых игральных костей?

10. Сколькими способами 2 монеты по 10 рублей, 4 монеты по 5 рублей и 5 монет по 1 рублю могут быть разложены по 3 разным кошелькам? (Пустые кошельки допускаются.)

11. Сколько решений в целых неотрицательных числах имеет неравенство ?

12. Функцией Эйлера 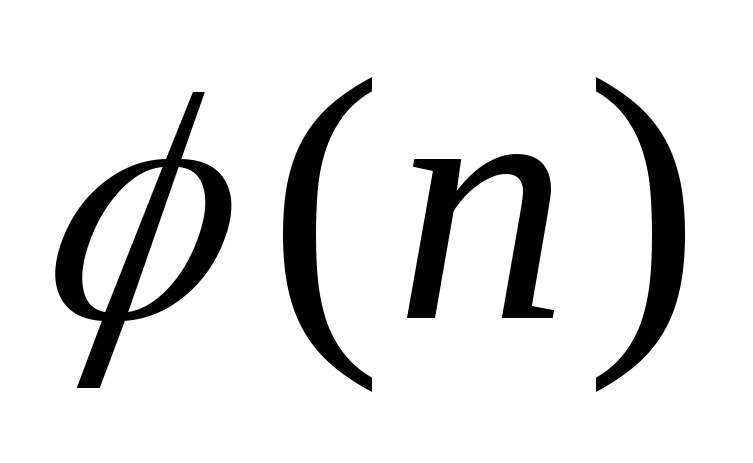для натуральныхназывается число натуральных чисел, не превосходящихи взаимно простых с. Показать, что при, гдевсе различные простые делители числа.

13. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека, если в каждой команде должно быть хотя бы по одному юноше?

14. В купе железнодорожного вагона имеются два противоположных дивана по 5 мест на каждом. Из 10 пассажиров этого купе четверо желают сидеть лицом по ходу движения, трое – спиной, а остальным безразлично как сидеть. Сколько способов размещения пассажиров с учетом их желаний существует?

15. Сколькими способами одинаковых шаров может быть разложено поразличным урнам?

16. Сколькими способами различных шаров может быть разложено поразличным урнам так, чтобы в первой урне оказалосьшаров, во второй –шаров и т.д., в-ой урне –шаров?

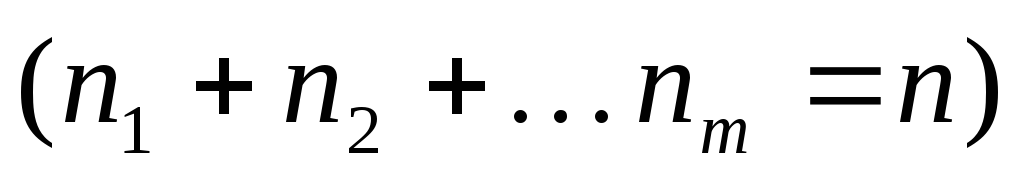17. Сколько натуральных чисел, не превосходящих 1000, не делятся ни на одно из чисел 6,10,15? а) 730; б) 732; в) 734.

18. Сколькими способами можно раздать 12 одинаковых монет 5 нищим так, чтобы каждый получил не менее одной, но не более 3 монет? а) 10; б) 20; в) 30.

19. В экзаменационную сессию поток студентов сдавал 4 предмета: математику, физику, химию и иностранный язык. Математику сдали на “отлично” 70% студентов, физику – 75%,химию – 80% и иностранный язык – 85%.Каков гарантированный процент студентов, получивших повышенную стипендию?

20. * Номера билетов состоят из 6 десятичных цифр, так что всего имеется 10⁶ номеров. Найти число «счастливых» номеров, у которых сумма первых трех цифр равна сумме последних трех цифр.

21. шаров шаров случайным образом размещаются по ящикам. Какова вероятность, что все ящики будут заняты?

22. Одновременно бросаются 3 кости. Какова вероятность, что на всех костях выпадет различное число очков?

23. На полу в беспорядке разбросаны пар туфель. Найти вероятность того, что среди двух наугад выбранных туфель одна окажется левой, а другая правой.

24. Найти вероятность того, что две наугад взятые костяшки домино можно приставить друг к другу.

25. * Из перетасованной колоды (36 карт) извлекаются 3 карты. Какова вероятность, что сумма их очков будет равна 21 (валет – 2, дама – 3, король – 4, туз – 11, остальные 6, 7, 8, 9, 10)?

26. Используется колода из 52 карт (достоинства карт начинаются с «двойки»). Карточные комбинации в вопросах задачи взяты из игры в покер, в которой играющий получает при сдаче 5 карт. Найти вероятность получить:

а) пять карт одной масти (флеш);

б) четыре карты из пяти одинакового достоинства (каре);

в) три карты одного достоинства и две другого (фул);

г) пять последовательных карт не одной масти (стрит);

д) три карты одного достоинства и две карты других различных между собой достоинств (тройка);

е) две карты одного достоинства и две карты другого достоинства плюс карта отличного от них достоинства (две двойки);

ж) две карты одного достоинства и три карты других различных между собой достоинств (двойка).

27. Найти -ый член последовательности, заданной рекуррентно,. а); б); в) 2ⁿ.

28. Найти ииз системы рекуррентных соотношений,. а); б)в).

29. С помощью производящих функций найти формулу для суммы кубов первых натуральных чисел.

30. Найти цикловой индекс группы самосовмещающих вращений тетраэдра, действующих на множестве его

а) граней;

б) ребер.

31. Найти число раскрасок ребер куба четырьмя цветами, использующих каждый

цвет трижды.

32.Найти число различных ожерелий из 8 бусинок – четырех синих и четырех

красных.