
- •6. Первообразная функции и неопределенный интеграл. Основные свойства таблицы интегралов.
- •7. Непосредственное интегрирование, замена переменной, интегрирование подведением под дифференциал.
- •8. Интегралы от нескольких функций, содержащих трехчлен. Интеграл простейших рациональных функций(1).
- •9. Интегралы от тригонометрических функций.
- •10. Две задачи, приводящих к понятию «интеграл». Свойства определенных интегралов. Интеграл с переменным верхним пределом.
- •I. Задача о массе стержня
- •II. Задача о пройденном пути
- •III. Задача о площади криволинейной трапеции
- •11. Формула Ньютона-Лейбница. Вычисление определенных интегралов. Приложение заданных интегралов к геометрическим и физическим задачам (объем, площадь, длины дуг, работа и т.Д.).(отдельный файл)
- •12. Приближенные вычисления определенных интегралов (формула трапеции, прямоугольника, параболы, трапеции Симпсона).
- •13. Несобственные интегралы (интеграл с бесконечными пределами или от неразрывных (неопределенных) функций). Сходимость интегралов, вычисление и оценка сходимости.
- •14. Двойной интеграл, определение, основные свойства, вычисление двойного интеграла в декартовых и полярных координатах.
- •15. Вычисление площади и объема посредством двойного интеграла.
Билеты по Высшей Математике
Функции многих переменных, область определения частные производные, полный дифференциал, частные производные высших порядков.
Функции многих переменных.
говорили
о функциях от одной переменной. Но можно
говорить также о функциях двух, трех и
вообще
![]() переменных.
переменных.
Функция
от двух переменных определяется следующим
образом. Рассматривается множество
![]() пар
чисел
пар
чисел![]() .
При этом имеются в виду упорядоченные
пары. Это значит, что две пары
.
При этом имеются в виду упорядоченные
пары. Это значит, что две пары![]() и
и![]() считаются
равными (совпадающими) тогда и только
тогда, когда
считаются
равными (совпадающими) тогда и только
тогда, когда![]() и
и![]() .
Если, в силу некоторого закона, каждой
паре
.
Если, в силу некоторого закона, каждой
паре![]() приведено
в соответствие число
приведено
в соответствие число![]() ,
то говорят, что этим определена на
множестве
,
то говорят, что этим определена на
множестве![]() функция
функция![]() от
двух переменных
от
двух переменных![]() и
и![]() .
.
Так
как каждой паре чисел
![]() соответствует
на плоскости, где введена декартова
система координат, точка с абсциссой
соответствует
на плоскости, где введена декартова
система координат, точка с абсциссой![]() и
ординатой
и
ординатой![]() ,
и, наоборот, каждой точке, таким образом,
соответствует пара
,
и, наоборот, каждой точке, таким образом,
соответствует пара![]() ,
то можно говорить, что наша функция
,
то можно говорить, что наша функция![]() задана
на множестве
задана
на множестве![]() точек
плоскости.
точек
плоскости.
Функцию
![]() от
двух переменных изображают в трехмерном
пространстве, где задана прямоугольная
система координат
от
двух переменных изображают в трехмерном
пространстве, где задана прямоугольная
система координат![]() ,
,![]() ,
,![]() ,
в виде геометрического места точек
,
в виде геометрического места точек![]() ,
проекции которых
,
проекции которых![]() принадлежат
множеству
принадлежат
множеству![]() определения
определения![]() .
.
Например, таким геометрическим местом для функции
![]() ,
,
является верхняя половина шаровой поверхности радиуса 1 с центром в нулевой точке.
В
этом же духе можно определить функцию
трех переменных. Областью ее определения
может теперь служить некоторое множество
упорядоченных троек чисел
![]() или,
что все равно, соответствующих им точек
трехмерного пространства, где введена
декартова система координат.
или,
что все равно, соответствующих им точек
трехмерного пространства, где введена
декартова система координат.
Если
каждой тройке чисел (точке трехмерного
пространства)
![]() ,
в силу некоторого закона, соответствует
число
,
в силу некоторого закона, соответствует
число![]() ,
то говорят, что этим на
,
то говорят, что этим на![]() определена
функция
определена
функция![]() .
.
Аналогично
можно рассматривать множество
![]() упорядоченных
систем
упорядоченных
систем![]() из
из![]() чисел,
где
чисел,
где![]() -
заданное натуральное число. Опять, если
каждой такой системе, принадлежащей
-
заданное натуральное число. Опять, если
каждой такой системе, принадлежащей![]() ,
соответствует в силу некоторого закона
число
,
соответствует в силу некоторого закона
число![]() ,
то говорят, что
,
то говорят, что![]() есть
функция от переменных
есть
функция от переменных![]() ,
определенная на множестве
,
определенная на множестве![]() ,
и записывается эта функция в виде
,
и записывается эта функция в виде![]() .
.
В
случае
![]() в
нашем распоряжении уже нет реального
в
нашем распоряжении уже нет реального![]() -
мерного пространства, чтобы использовать
его для изображения систем
-
мерного пространства, чтобы использовать
его для изображения систем![]() в
виде принадлежащих ему точек. Но
математики выдумали
в
виде принадлежащих ему точек. Но
математики выдумали![]() -мерное
пространство, и оно им благополучно
служит, и притом не хуже, чем реальное
трехмерное пространство. Именно,
-мерное
пространство, и оно им благополучно
служит, и притом не хуже, чем реальное
трехмерное пространство. Именно,![]() -мерным
пространством называется множество
всевозможных систем
-мерным
пространством называется множество
всевозможных систем![]() чисел
чисел![]() .
.
Если
две функции
![]() и
и![]() от
от![]() переменных
заданы на одном и том же множестве
переменных
заданы на одном и том же множестве![]() систем
систем![]() -
точек
-
точек![]() -мерного
пространства, - то можно определить
сумму
-мерного
пространства, - то можно определить
сумму![]() ,
разность
,
разность![]() ,
произведение
,
произведение![]() и
частное
и
частное![]() ,
как функции, определенные на
,
как функции, определенные на![]() при
помощи равенств, аналогичных равенствам
(2), где надо только числа
при
помощи равенств, аналогичных равенствам
(2), где надо только числа![]() заменить
системами
заменить
системами![]() .
Естественным образом определяются
также сложные функции, такие, как
.
Естественным образом определяются
также сложные функции, такие, как![]() ,
где
,
где![]() -
тройки чисел, принадлежащих некоторому
множеству троек.
-
тройки чисел, принадлежащих некоторому
множеству троек.
Ниже приводится несколько примеров функций многих переменных, заданных посредством элементарных формул.
П
р и м е р 8.
![]() ,
где
,
где![]() ,
,![]() ,
,![]() ,
,![]() -
заданные постоянные действительные
числа, есть линейная функция от трех
переменных
-
заданные постоянные действительные
числа, есть линейная функция от трех
переменных![]() .
Она задана на всем трехмерном пространстве.
Более общая линейная функция от
.
Она задана на всем трехмерном пространстве.
Более общая линейная функция от![]() переменных
переменных![]() задается
формулой
задается
формулой ,
где
,
где![]() -
заданные постоянные числа. Эта функция
определена в любой точке
-
заданные постоянные числа. Эта функция
определена в любой точке![]()
![]() -мерного
пространства, или, как еще говорят, на
всем
-мерного
пространства, или, как еще говорят, на
всем![]() -
мерном пространстве.
-
мерном пространстве.
П
р и м е р 9.
![]() .
Эта действительная функция задана на
области, представляющей собой круг
радиуса 1 с центром в
.
Эта действительная функция задана на
области, представляющей собой круг
радиуса 1 с центром в![]() ,
из которого удалены все граничные точки,
т. е. точки окружности радиуса 1 с центром
,
из которого удалены все граничные точки,
т. е. точки окружности радиуса 1 с центром![]() .
Для этих точек наша функция не определена,
потому что
.
Для этих точек наша функция не определена,
потому что![]() не
имеет смысла.
не
имеет смысла.
П р и м е р 10. Функция

геометрически
изображается двумя параллельными
полуплоскостями, не связанными между
собой. Расположение их по отношению к
системе координат
![]() очевидно.
очевидно.
Функция от одной переменной может быть задана неявным образом при помощи равенства
![]() ,
(3)
,
(3)
где
![]() есть
функция от двух переменных
есть
функция от двух переменных![]() и
и![]() .
.
Пусть
на некотором множестве
![]() точек
точек![]() задана
функция
задана
функция![]() .
Равенство (3) определяет некоторое
подмножество
.
Равенство (3) определяет некоторое
подмножество![]() множества
множества![]() ,
на котором функция
,
на котором функция![]() равна
нулю. Конечно, в частности,
равна
нулю. Конечно, в частности,![]() может
быть пустым множеством. Пусть
может
быть пустым множеством. Пусть![]() -
непустое множество, и пусть
-
непустое множество, и пусть![]() -
множество (очевидно, непустое) таких
значений
-
множество (очевидно, непустое) таких
значений![]() (чисел),
которым соответствует хотя бы одно
(чисел),
которым соответствует хотя бы одно![]() так,
что пара
так,
что пара![]() ,
,![]() принадлежит
принадлежит![]() .
Таким образом,
.
Таким образом,![]() есть
множество всех чисел
есть
множество всех чисел![]() ,
каждому из которых соответствует
непустое множество
,
каждому из которых соответствует
непустое множество![]() чисел
чисел![]() так,
что
так,
что![]() ,
или, что все равно, так, что для указанной
пары
,
или, что все равно, так, что для указанной
пары![]() выполняется
равенство (3). Этим определена на множестве
выполняется
равенство (3). Этим определена на множестве![]() некоторая
функция
некоторая
функция![]() от
от![]() ,
вообще говоря, многозначная. В таком
случае говорят, что функция
,
вообще говоря, многозначная. В таком
случае говорят, что функция![]() определена
неявно при помощи равенства (3). Для нее,
очевидно, выполняется тождество
определена
неявно при помощи равенства (3). Для нее,
очевидно, выполняется тождество
![]() для
всех
для
всех
![]() .
.
По
аналогии можно также определить фуекцию
![]() от
переменной
от
переменной![]() ,
определяемую неявно при помощи равенства
(3). Для нее выполняется тождество
,
определяемую неявно при помощи равенства
(3). Для нее выполняется тождество
![]() для
всех
для
всех
![]() ,
,
где
![]() -
некоторое множество чисел. Говорят еще,
что функция
-
некоторое множество чисел. Говорят еще,
что функция![]() (или
(или![]() )
удовлетворяет уравнению (3). Функцию
)
удовлетворяет уравнению (3). Функцию![]() называют
обратной по отношению к функции
называют
обратной по отношению к функции![]() .
.
П р и м е р 11. Уравнение
![]() ,
(4)
,
(4)
где
![]() ,
неявно определяет двузначную функцию
от одной переменной:
,
неявно определяет двузначную функцию
от одной переменной:
![]() ;
;
впрочем,
при
![]() она
однозначна. Естественно считать, что
эта двузначная функция распадается на
две непрерывные однозначные функции
она
однозначна. Естественно считать, что
эта двузначная функция распадается на
две непрерывные однозначные функции![]() и
и![]()
![]() .
Графики их (полуокружности) в совокупности
дают окружность радиуса
.
Графики их (полуокружности) в совокупности
дают окружность радиуса![]() с
центром в начале координат. Эта окружность
есть геометрическое место точек,
координаты
с
центром в начале координат. Эта окружность
есть геометрическое место точек,
координаты![]() которых
удовлетворяют уравнению (4). Но можно,
пользуясь формулой (4), конструировать
различные однозначные (разрывные)
функции, удовлетворяющие уравнению
(4). Например, такой является функция
которых
удовлетворяют уравнению (4). Но можно,
пользуясь формулой (4), конструировать
различные однозначные (разрывные)
функции, удовлетворяющие уравнению
(4). Например, такой является функция

Скалярное поле(2), поверхности и линии уровня(1), производные по направлению(4), градиент скалярного поля(3).
Рассмотрим
в 3-х мерном пространстве некоторую
область. Если в каждой точке
![]() этой
области задать число (скаляр)
этой
области задать число (скаляр)![]() ,
то говорят, что заданоскалярное
поле
,
то говорят, что заданоскалярное
поле
![]() .
Согласно такому определению, скалярное
поле является функцией точки. Так как
положение точки
.
Согласно такому определению, скалярное
поле является функцией точки. Так как
положение точки![]() можно
характеризовать ее радиус-вектором
можно
характеризовать ее радиус-вектором![]() ,
то задание поля будет означать, что
установлено соответствие между
,
то задание поля будет означать, что
установлено соответствие между![]() и
и![]() .
Таким образом, поле можно рассматривать
как функцию векторного аргумента
.
Таким образом, поле можно рассматривать
как функцию векторного аргумента![]() (рис.13).
(рис.13).

Рис.13. К определению скалярного поля
Если
в области определения поля ввести
декартову систему координат, то
![]() можно
представить как упорядоченную тройку
чисел
можно
представить как упорядоченную тройку
чисел![]() и
тогда задание поля будет эквивалентно
заданию функции трех переменных
и
тогда задание поля будет эквивалентно
заданию функции трех переменных![]() .
В дальнейшем будем считать эту функцию
непрерывной и дифференцируемой.
.
В дальнейшем будем считать эту функцию
непрерывной и дифференцируемой.
Как
известно, функцию одной переменной
можно рассматривать как уравнение
кривой на плоскости
![]() ,
двух переменных - как поверхность
,
двух переменных - как поверхность![]() .
Представить аналогичный "график"
в случае поля
.
Представить аналогичный "график"
в случае поля![]() затруднительно,
поэтому для наглядной характеристики
поля используютповерхности
уровня.
затруднительно,
поэтому для наглядной характеристики
поля используютповерхности
уровня.
Поверхностью
уровня поля
![]() называют
геометрическое место точек, в которых
поле принимает постоянное значение.
Согласно такому определению, уравнение
поверхности уровня будет иметь вид:
называют
геометрическое место точек, в которых
поле принимает постоянное значение.
Согласно такому определению, уравнение
поверхности уровня будет иметь вид:
|
|
(61) |
Уравнение
(61)
является уравнением поверхности, что
объясняет соответствующее название.
Придавая
![]() различные
значения, можно получить наглядное
представление о том, как величина
различные
значения, можно получить наглядное
представление о том, как величина![]() распределена
в пространстве. При этом, если в некоторой
области поле изменяется быстро,
поверхности уровня будут сближаться.
Пересекаться они не могут, за исключением
одной точки.
распределена
в пространстве. При этом, если в некоторой
области поле изменяется быстро,
поверхности уровня будут сближаться.
Пересекаться они не могут, за исключением
одной точки.

Рис.14. Поверхности уровня скалярного поля.
Пример
2-2.
Рассмотрим поле вида
![]() (или
просто
(или
просто![]() ).
Уравнение (61)
принимает вид:
).
Уравнение (61)
принимает вид:
![]()
Так
как
![]() ,
то
,
то

и,
таким образом, поверхностями уровня
поля
![]() будет
семейство концентрических сфер с центром
в начале координат (рис.14).
будет
семейство концентрических сфер с центром
в начале координат (рис.14).
Пример
2-3.
Построить линии уровня плоского поля
 ,
где
,
где![]() ,
,![]() ,
,![]() (2-х
мерный аналог потенциала электрического
диполя).
(2-х
мерный аналог потенциала электрического
диполя).
Решение. Уравнение линий уровня имеет вид:


рис.15. Линии уровня плоского поля.
Для
различных значений
![]() получается
семейство окружностей с единственной
общей точкой в начале координат (рис.15).
В левой полуплоскости значения поля
положительно, в правой - отрицательно,
а в точке
получается
семейство окружностей с единственной
общей точкой в начале координат (рис.15).
В левой полуплоскости значения поля
положительно, в правой - отрицательно,
а в точке
![]() поле
имеет особенность и неопределено.
поле
имеет особенность и неопределено.
СКАЛЯРНОЕ ПОЛЕполе физическое, к-рое описывается ф-цией, в каждой точке пр-ва не изменяющейся при повороте системы координат. В квант. теории поля квантами С. п. явл. ч-цы со спином 0. По поведению относительно пространственной инверсии С. п. делят на собственно скалярные, если полевая ф-ция не меняет знака при инверсии, и псевдоскалярные, если меняет. Отвечающие им ч-цы имеют соответственно положит. и отрицат. внутр. чётность и наз. скалярными (напр., e-мезон) и псевдоскалярными (напр., p-, К-, h-мезоны).
СКАЛЯРНОЕ ПОЛЕ
-
поле
физическое,
к-рое описываетсяф-цией координат
пространства-времени х=
( х,
t),
не изменяющейсяпри поворотах системы
координат. Свободные (невзаимодействующие)
поля подчиняются Клейна-
Гордона уравнению
![]()
где
![]() -Д'Аламбера
оператор,
а параметр т
наз. массой (ур-ние записанов системе
-Д'Аламбера
оператор,
а параметр т
наз. массой (ур-ние записанов системе
![]() ).
Общее решение (*) имеет вид суперпозиции
плоских волн с волновым векторомk
и частотой
).
Общее решение (*) имеет вид суперпозиции
плоских волн с волновым векторомk
и частотой
![]() (нулевой
компонентой 4-вектораk):
(нулевой
компонентой 4-вектораk):

В
квантовой
теории поля
ф-ции
![]() представляют
собойоператоры
рождения и уничтожения свободных
скалярныхчастиц с импульсом k, массой
т
и нулевым спином, являющихся квантамиС.
п. Для взаимодействующего С. п. в правой
части ур-ния (*) стоит выражение, <нелинейно
зависящее от самого поля
представляют
собойоператоры
рождения и уничтожения свободных
скалярныхчастиц с импульсом k, массой
т
и нулевым спином, являющихся квантамиС.
п. Для взаимодействующего С. п. в правой
части ур-ния (*) стоит выражение, <нелинейно
зависящее от самого поля
![]() (случай
самодействия, напр.:
(случай
самодействия, напр.:![]() ,гдеg -
константа взаимодействия) или от др.
физ. полей. По поведениюотносительно
пространственной
инверсии
С. п. делят на собственноскалярные
,гдеg -
константа взаимодействия) или от др.
физ. полей. По поведениюотносительно
пространственной
инверсии
С. п. делят на собственноскалярные
![]() и
псевдоскалярные
и
псевдоскалярные![]() .
Отвечающие имэлементарные
частицы
имеют соответственно положительнуюи
отрицательную внутреннюю
чётность
и наз. скалярными
частицами
ипсевдоскалярными частицами (напр.,
.
Отвечающие имэлементарные
частицы
имеют соответственно положительнуюи
отрицательную внутреннюю
чётность
и наз. скалярными
частицами
ипсевдоскалярными частицами (напр.,![]() K,
K,![]() ).
А. <В. Ефремов.
).
А. <В. Ефремов.
Пусть
в некоторой области 3-х мерного пространства
задано скалярное поле
![]() .
Выберем в этой области точку
.
Выберем в этой области точку![]() .
Если перемещаться из этой точки вдоль
какой-либо линии, то поле будет меняться
от точки к точке. Причем, ясно, что для
различных направлений скорость изменения
.
Если перемещаться из этой точки вдоль
какой-либо линии, то поле будет меняться
от точки к точке. Причем, ясно, что для
различных направлений скорость изменения![]() также
может оказаться различной и должна
характеризовать само поле в рассматриваемой
точке или ее окрестности. При этом, по
смыслу рассуждений, эта величина должна
быть векторной. Рассмотрим строгое
определение этой характеристики на
примере гидромеханической аналогии.
Пусть в пространстве задано скалярное
поле давления жидкости или газа. Поместим
в эту область тело произвольной формы,
ограниченное поверхностью
также
может оказаться различной и должна
характеризовать само поле в рассматриваемой
точке или ее окрестности. При этом, по
смыслу рассуждений, эта величина должна
быть векторной. Рассмотрим строгое
определение этой характеристики на
примере гидромеханической аналогии.
Пусть в пространстве задано скалярное
поле давления жидкости или газа. Поместим
в эту область тело произвольной формы,
ограниченное поверхностью![]() ,
(рис.24).
Вычислим суммарую силу
,
(рис.24).
Вычислим суммарую силу
![]() ,
действующую на тело со стороны среды.
,
действующую на тело со стороны среды.

Рис.24 К определению градиента скалярной функции
Рассмотрим
площадку
![]() ,
содержащую точку
,
содержащую точку![]() на
поверхности
на
поверхности![]() .
Модуль силы, действующей на площадку
.
Модуль силы, действующей на площадку![]() ,
равен
,
равен![]() ,
а направление совпадает с направлением
нормали к поверхности в точке
,
а направление совпадает с направлением
нормали к поверхности в точке![]() .
Таким образом, вектор силы
.
Таким образом, вектор силы
|
|
(71) |
Полная
сила может быть вычислена интегрированием
по поверхности
![]() :
:
|
|
(72) |
Если
результат (72)
разделить на объем
![]() ,
заключенный внутри поверхности
,
заключенный внутри поверхности![]() ,
то получившаяся величина
,
то получившаяся величина
|
|
(73) |
будет
"средней" силой, действующей со
стороны среды на любую точку внутри
![]() .
Физической причиной этого действия
является перепад давлений между
различными точками среды.
.
Физической причиной этого действия
является перепад давлений между
различными точками среды.
Способность
поля (в данном случае поля давлений)
оказывать действие на пробное тело
является характеристикой самого поля
и поэтому не должна зависеть на формы
и размеров тела, помещенного в это поле.
Будем стягивать поверхность
![]() к
точке
к
точке![]() ,
устремляя, таким образом,
,
устремляя, таким образом,![]() и
рассмотрим предел
и
рассмотрим предел
|
|
(74) |
Если
предел (74)
существует, то по смыслу рассуждений
он определит плотность силы, действующей
со стороны поля (давлений) на точечное
тело, помещенное в точку
![]() и
будет характеризовать быстроту изменения
поля (перепад давлений) в окрестности
этой точки.
и
будет характеризовать быстроту изменения
поля (перепад давлений) в окрестности
этой точки.
Рассмотрим
общий случай скалярного поля
![]() .
Если для поля
.
Если для поля![]() существует
предел (74)
при стягивании поверхности к точке
существует
предел (74)
при стягивании поверхности к точке
![]() ,
то он называетсяградиентом
поля
,
то он называетсяградиентом
поля
![]() в
этой точке:
в
этой точке:
|
|
(75) |
По
определению
![]() является
вектором и вообще, выражение (75),
будучи примененным в каждой точке
области определения поля
является
вектором и вообще, выражение (75),
будучи примененным в каждой точке
области определения поля
![]() ,
будет задавать векторное поле градиента
,
будет задавать векторное поле градиента![]() .
.
Формула
(75)
задает определение
![]() в
форме, независящей от системы координат
- инвариантно. Пользуясь (75),
получим формулу вычисления градиента
скалярного поля в декартовой системе
координат. Тогда, так как вектор нормали
в
форме, независящей от системы координат
- инвариантно. Пользуясь (75),
получим формулу вычисления градиента
скалярного поля в декартовой системе
координат. Тогда, так как вектор нормали
![]() :
:
|
|
(76) |
Применим к каждому слагаемому (76) формулу Остроградского-Гаусса (3.1):
|
|
(77) |
Применяя теорему о среднем к правой части (77), получим
|
|
(78) |
переходя
к пределу
![]() и
сравнивая с определением градиента
(75),
получим формулу
для вычисления градиента в декартовой
системе координат:
и
сравнивая с определением градиента
(75),
получим формулу
для вычисления градиента в декартовой
системе координат:
|
Производная
по направлению.
Выберем в пространстве, где задано
скалярное поле
Полученное
выражение, учитывая, что
Это
выражение (81)
называется производной
по направлению
Из определения (81) следуют свойства градиента:
Формула
(79)
позволяет получить следующие свойства
и правила вычисления
Пример
3-8.
Вычислить градиент поля
Решение. Согласно выражению (79), получим
Аналогично,
|
3. Формула Тейлора для функции двух переменных. Экстремум функции двух независимых переменных, необходимые и достаточные условия. (http://glaznev.sibcity.ru/1kurs/fmp/htm_fmp/fmp_lek5.htm- не копируется инфа)
Формула Тейлора
Рассмотрим
пару
![]() :
:![]()
![]()
![]()
![]()
Так
как мы делали линейную замену, можно
просто подставить
![]() обратно,
тогда получим:
обратно,
тогда получим:
![]() —формула
Тейлора для функции многих переменных.
—формула
Тейлора для функции многих переменных.
В
частности, при
![]() :
:
![]()
Определение точки экстремума функций двух переменных:
Говорят,
что функция
![]() имеет
в
имеет
в
![]() максимум
(минимум) если существует такая окрестность
точки
максимум
(минимум) если существует такая окрестность
точки
![]() ,
что для любой
,
что для любой![]() из
неё выполняется неравенство
из
неё выполняется неравенство![]()
![]()
Необходимое условие существования:
Пусть
функция
![]() имеет
в
имеет
в![]() экстремум.
Тогда
экстремум.
Тогда![]() и
и![]() либо
равны 0, либо равны
либо
равны 0, либо равны![]() ,
либо не существуют.
,
либо не существуют.
Замечание:
Если
![]() -
дифференцируемая в
-
дифференцируемая в![]() ,
то
,
то![]() .
.
Достаточное условие существования:
Пусть
![]() –
стационарная точка, дважды непрерывно
дифференцируемой функции
–
стационарная точка, дважды непрерывно
дифференцируемой функции![]() .
Если число
.
Если число![]() ,
то в
,
то в![]() функция
имеет экстремум.
функция
имеет экстремум.
|
|
|
|
|
|
|
|
Экстремума нет |
Требуются доп. исследования |
|
|
|
Экстремума нет |
4. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала.
Касательная плоскость и нормаль к поверхности.
Касательная
плоскость к поверхности в её точке![]() (точка
касания) есть плоскость, проходящая
через
(точка
касания) есть плоскость, проходящая
через![]() и
содержащая в себе все касательные,
проведённые в точке
и
содержащая в себе все касательные,
проведённые в точке![]() ко
всевозможным кривым, проведённым на
поверхности через точку
ко
всевозможным кривым, проведённым на
поверхности через точку
![]()
Нормалью
к поверхности в точке![]() называется
прямая, проходящая через точку
называется
прямая, проходящая через точку
![]() и
перпендикулярная к касательной плоскости,
проведённой в этой точке.
и
перпендикулярная к касательной плоскости,
проведённой в этой точке.
Если
уравнение поверхности имеет вид F(x,
y, z)=0, то
уравнение касательной плоскости в точке
![]() имеет
вид:
имеет
вид:
![]()
Уравнение
нормали к этой поверхности в точке
![]() есть
есть

В случае явного задания поверхности уравнением (8.1) и (8.2) примут вид

Пример решений
Пример
7.1. Найти
уравнение касательной плоскости и
уравнение нормали к поверхности
![]() в
точке
в
точке![]()
Решение: Имеем

Тогда, согласно (8.3) уравнение касательной плоскости к данной поверхности в указанной точке будет иметь вид: z - 6 = - 4(x + 1) + 2(y - 2), то есть 4x - 2y + z + 2 = 0, а уравнение нормали

Пример 7.2. Найти уравнение касательной плоскости и нормали к косинусу

Решение. Имеем
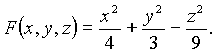
Тогда

Уравнение касательной плоскости запишем в виде

ИЛИ
Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.

Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
![]() .
.
Уравнение нормали к поверхности в этой точке:
![]()
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+х, у0+у).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
![]()
в точке М(1, 1, 1).
![]()
![]()
Уравнение касательной плоскости:
![]()
Уравнение нормали:
![]()
5. Метод наименьших квадратов.
В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей.
![]()
Иными словами, из всего множества линий, линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:
![]()
следовательно
![]()

Целью процедур линейной регрессии является подгонка прямой линии по точкам. А именно, построить линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов. Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=ax+b
6. Первообразная функции и неопределенный интеграл. Основные свойства таблицы интегралов.
Определение первообразной.
Первообразной
функции f(x)
на промежутке (a;
b)
называется такая функция F(x),
что выполняется равенство
![]() для
любогох
из заданного промежутка.
для
любогох
из заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С
равна нулю, то справедливо равенство
![]() .
Таким образом, функцияf(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функцияf(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным интегралом
этой функции и обозначается
![]() .
.
Выражение
![]() называютподынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называютподынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
![]() Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.
![]() Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
![]() ,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
![]() Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для
доказательства третьего и четвертого
свойств достаточно найти производные
от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
Рассмотрим пример.
Пример.
Найти
первообразную функции
![]() ,
значение которой равно единице прих
= 1.
,
значение которой равно единице прих
= 1.
Решение.
Мы
знаем из дифференциального исчисления,
что
![]() (достаточно
заглянуть в таблицу производных основных
элементарных функций). Таким образом,
(достаточно
заглянуть в таблицу производных основных
элементарных функций). Таким образом,![]() .
По второму свойству
.
По второму свойству![]() .
То есть, имеем множество первообразных
.
То есть, имеем множество первообразных![]() .
Прих
= 1
получим значение
.
Прих
= 1
получим значение
![]() .
По условию, это значение должно быть
равно единице, следовательно,С
= 1.
Искомая первообразная примет вид
.
По условию, это значение должно быть
равно единице, следовательно,С
= 1.
Искомая первообразная примет вид
![]() .
.
Ниже выписана основная таблица неопределенных интегралов, в данной таблице приведены неопределенные интегралы от основных функций. Вычисление (взятие) интегралов заключается в том, чтобы специальными методами (заменами переменных) свести данный неопределенный интеграл к уже известному (существующему) интегралу, т.е. неопределенному интегралу из данной таблицы интегралов.
 где
где![]()













Здесь C - произвольная постоянная, т.к. производная от постоянной есть нуль, следовательно, неопределенный интеграл определяется с точностью до постоянной.
Операция интегрирования функции обладает некоторыми свойствами, которые помогают при вычислении неопределенных интегралов. Ниже выписана таблица основных свойств интегралов.
Данные свойства позволяют свести исходный неопределенный интеграл к серии более легких и простых интегралов, которые берутся из основной таблицы неопределенных интегралов.


 где
где![]()

Здесь C-произвольная постоянная, т.к. производная от постоянной есть нуль, следовательно, неопределенный интеграл определяется с точностью до постоянной.





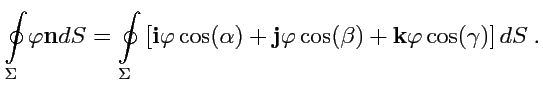


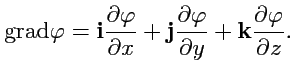


 (сложное
поле)
(сложное
поле)

 ,
, и
тогда, складывая вычисленные
производные, получим:
и
тогда, складывая вычисленные
производные, получим: или
в бескоординатной форме
или
в бескоординатной форме