
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Московский государственный университет технологий и управления
имени К.Г. Разумовского»
Филиал ФГБОУ ВПО «МГУТУ им. К.Г. Разумовского» в г. Мелеузе
(Республика Башкортостан)
Контрольная работа
по дисциплине: Методы оптимизации
на тему: вариант №6
Выполнил:
Студент____3____курса
Абсалямов Р.М._________
Института: САиИ______
Специальность:220700 (збс)
Шифр:___986_________
Работа сдана на проверку:
Преподаватель:
Оценка:__________
Мелеуз 2013
Содержание
1.Задача 1.6…………………………………………………………………….3
2.Задача 2.6…………………………………………………………………….7
3.Задача 3.6……………………………………………………………………11
4.Задача 4.6…………………………………………………………………....13
Список использованной литературы………………………………………...15
1.Задача 1.6
Используя
три приведенных способа выбора
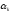 ,
найти минимум функций градиентным
методом и сравнить полученные решения.
Начальную точкуx,
параметры
,
найти минимум функций градиентным
методом и сравнить полученные решения.
Начальную точкуx,
параметры
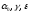 выбрать самостоятельно.
выбрать самостоятельно.
|
Решение:
Вычислим градиент и норму для рассматриваемой функции:
Итерационный процесс минимизации с использованием нормированого антиградиента в координатной форме запишется:
В
качестве начальной точки возьмем
Рассмотрим
три способа выбора
Фиксированная
длина шага
В
качестве
|
|
Таблица 1.1
|
Номер интерации |
x1k |
x2k |
df(xk)/dx1 |
df(xk)/dx2 |
||f҆҆҆ ′(xk)|| |
f(xk) |
|
0 |
2 |
2 |
10 |
-2 |
9,797959 |
-4 |
|
1 |
0,979379 |
2,204124 |
-0,20621 |
-1,59175 |
1,605053 |
-9,36446 |
|
2 |
1,107853 |
3,195837 |
1,078531 |
0,391674 |
1,147448 |
-9,90349 |
|
3 |
0,167914 |
2,854493 |
-8,32086 |
-0,29101 |
8,325942 |
-6,517 |
|
4 |
1,167303 |
2,889446 |
1,673035 |
-0,22111 |
1,687582 |
-9,84783 |
|
5 |
0,175924 |
3,020467 |
-8,24076 |
0,040933 |
8,240863 |
-6,60407 |
|
6 |
1,175911 |
3,015499 |
1,759115 |
0,030999 |
1,759388 |
-9,84504 |
Из
результатов, приведенных в таблице 1
видно, что при выбранном постоянном
шаге условие останова никогда не
выполнится, так как вычисленный процесс
в заключительной стадии сопровождается
колебаниями «вперед-назад» на одних и
тех же точках. Для того, чтобы получить
решение с требуемой точностью (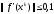 )
нужно взять меньшую длину фиксированного
шага
)
нужно взять меньшую длину фиксированного
шага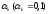 ,
но тогда скорость сходимости будет
невысокой и для решения задачи потребуется
большое число итераций.
,
но тогда скорость сходимости будет
невысокой и для решения задачи потребуется
большое число итераций.
Последовательное
(поитерационное) уменьшение
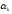 .
.
Зададим
некоторое значение
 и далее величина шага будет поитерационно
уменьшается по формуле
и далее величина шага будет поитерационно
уменьшается по формуле
Для рассматриваемого
примера положим
 и результаты расчета оформить в таблице
2.
и результаты расчета оформить в таблице
2.
|
Номер интера-ции |
x1k |
x2k |
αk |
df(xk)/dx1 |
df(xk)/dx2 |
||f҆҆҆ ′(xk)|| |
f(xk) |
|
0 |
2 |
2 |
2 |
10 |
-2 |
9,797959 |
-4 |
|
1 |
-0,04124 |
2,408248 |
1 |
-10,4124 |
-1,1835 |
10,47946 |
-4,22891 |
|
2 |
0,952361 |
2,521184 |
0,5 |
-0,47639 |
-0,95763 |
1,069583 |
-9,75939 |
|
3 |
1,17506 |
2,96885 |
0,25 |
1,750604 |
-0,0623 |
1,751712 |
-9,8458 |
|
4 |
0,925219 |
2,977741 |
0,125 |
-0,74781 |
-0,04452 |
0,749138 |
-9,97154 |
|
5 |
1,049998 |
2,985169 |
0,0625 |
0,499976 |
-0,02966 |
0,500855 |
-9,98728 |
|
6 |
0,987607 |
2,988871 |
0,03125 |
-0,12393 |
-0,02226 |
0,12591 |
-9,99911 |
|
7 |
1,018365 |
2,994395 |
0,01562 |
0,183651 |
-0,01121 |
0,183993 |
-9,99828 |
|
8 |
1,002769 |
2,995347 |
- |
0,027692 |
-0,00931 |
0,029214 |
-9,99994 |
Второй
способ выбора
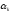 оказался лучше предыдущего – позволяет
найти точку минимума с любой заданной
точностью.
оказался лучше предыдущего – позволяет
найти точку минимума с любой заданной
точностью.
Определение
оптимального значения

Если
 выбирается из условия
выбирается из условия
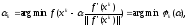 (1)
(1)
то указанная модификация градиентного метода носит название метода наискорейшего спуска.
Выполним
расчеты на нулевой итерации. В исходной
точке
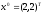 нормированный градиент равен (0,9806,
-0,1961). Тогда
нормированный градиент равен (0,9806,
-0,1961). Тогда
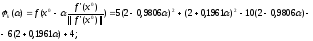
Вычислим
производную по
 от полученной функции и приравняем её
к нулю:
от полученной функции и приравняем её
к нулю:
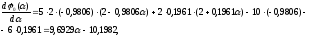
откуда
получаем искомое значение
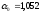 .
.
Определим
следующую точку

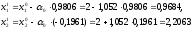
Вычислим
градиент в точке
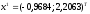
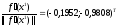
построим

Вычислим
производную по
 от полученной функции и приравняем её
к нулю:
от полученной функции и приравняем её
к нулю:
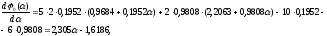
Определим
искомое значение

Аналогичным построением позволяют на 4-й итерации добиться решения задачи (таблица 3)
Таблица 3
|
k |
x1k |
x2k |
df(xk)/dx1 |
df(xk)/dx2 |
||f′(xk)|| |
αk |
f(xk) |
|
0 |
2 |
2 |
10 |
-2 |
10,198 |
1,052 |
-4 |
|
1 |
0,968429 |
2,206314 |
-0,31571 |
-1,58737 |
1,61846 |
0,702 |
-9,36508 |
|
2 |
1,105366 |
2,894829 |
1,053662 |
-0,21034 |
1,07445 |
0,11 |
-9,93343 |
|
3 |
0,997495 |
2,916363 |
-0,02505 |
-0,16727 |
0,16914 |
0,078 |
-9,99297 |
|
4 |
1 |
3 |
0 |
0 |
0 |
0 |
-10 |
|
k |
f′(x1)/||f′(x1)|| |
f′(x2)/||f′(x2)|| |
|
0 |
0,980580676 |
-0,1961161 |
|
1 |
-0,195067056 |
-0,9807899 |
|
2 |
0,980650378 |
-0,1957673 |
|
3 |
-0,148122568 |
-0,988969 |
|
4 |
- |
- |
Метод наискорейшего спуска обладает большей скоростью сходимости по сравнению с двумя предыдущими методами.
Ответ:

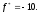

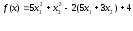
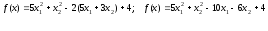


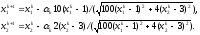
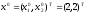 ,
а правилом останова служит выполнение
неравенства
,
а правилом останова служит выполнение
неравенства .
.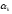 .
.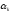 .
.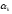 возмем некоторое постоянное для всех
итераций значение. Например, возьмем
возмем некоторое постоянное для всех
итераций значение. Например, возьмем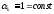 для всех
для всех и результаты расчета запишем в таблицу
1.1.
и результаты расчета запишем в таблицу
1.1.