Математическая логика и теория

Федеральное агентство по образованию

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ

(образован в 1953 году)

Кафедра физики и высшей математики

Дистанционное обучение

Физ. мат. 8.03.2202 зчн.скр. Физ. мат. 8.03.2202 зчн.плн.

Физ. мат. 8.03.2202 зчн.плн. Физ. мат. 8.03.2202 зчн.скр.

А.Р. Садыкова

Математическая логика и теория

алгоритмов

Рабочая программа и методические указания по выполнению

контрольных заданий студентами специальности 2202 (230102)заочной формы обучения

www.msta.ru

Москва – 2007

УДК 519.6

3-93

 Садыкова А.Р. «Математическая логика и теория алгоритмов». Контрольные задания для студентов-заочников специальности 2202 (230102), М.: МГУТУ, 2007.

Настоящее пособие предназначено для студентов специальности 2202 (230102) заочной формы обучения. Пособие содержит рабочую программу, методические указания по выполнению контрольной работы, а также текст самой контрольной работы, представленной в 10 вариантах

Автор к.п.н., доцент кафедры Садыкова Альбина Рифовна.

Рецензент д.ф-м.н., проф. Зуев Ю.А.

Редактор Свешникова Н.И.

Московский государственный университет технологий и управления, 2007

109004, Москва, Земляной вал, 73.

Рабочая программа

1. Множества.

1. Операции над множествами.

2. Мощность множества.

3. Прямое произведение множеств.

2. Отношения, функции, алгебраические структуры, морфизмы.

1. Бинарные отношения и функции.

2. Алгебраические структуры и морфизмы.

3. Алгебра высказываний.

1. Исчисление высказываний.

2. Предикаты и кванторы.

3. Булевы алгебры.

4. Метод математической индукции.

4. Булевы функции.

1. ДНФ и КНФ.

2. Упрощение ДНФ.

3. Полином Жегалкина.

4. Полнота функций.

5. Алгоритмы.

1. Понятие алгоритма.

2. Алгоритм Евклида.

3. Машина Тьюринга.

4. Алгоритмически неразрешимые проблемы.

Рекомендуемая литература

1. Колмагоров А.Н., Драгалин А.Г. Математическая логика. – М.: Едиториал УРСС, 2004. – 240 с.

2. Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. – 2-е изд. – М.: Физматлит, 2002. – 128 с.

3. Лавров И.А. Максимова Л.Л. Задачи по теории множеств математической логике и теории алгоритмов. – 4-е изд. – М.: Физматлит, 2001. – 256 с.

4. Шапорев С.Д. Математическая логика. Курс лекций и практических занятий. – СПб.: БХВ – Петербург, 2005.- 416 с.: ил.

ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ

СО СТУДЕНТАМИ заочного ФАКУЛЬТЕТА

специальности 230102 (2202) полной [сокращенной] ФОРМЫ ОБУЧЕНИЯ

№	ТЕМА	ЛЕКЦИИ	ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
1	Булевы функции. Операции . Правило де Моргана. Двойственность, К.Н.Ф. и Д.Н.Ф.	4 [2]	2 [2]
2	Кванторы и Предикаты. Логика высказываний и логика предикатов.	4 [2]	2 [2]
3	Машина Тьюринга и понятие алгоритма. Неразрешимость проблемы останова.	4 [2]	2 [2]
4	Эффективность алгоритма. Линейное упорядочивание массива за время О (n long).	1 [-]	0,5 [-]
5	Графы: планарные, регулярные, эйлеровы, гамильтоновы, ориентированные, циклы, деревья, клики, независимые множества, вершинное покрытие.	2 [2]	2 [0,5]
6	Алгоритмы на графах: кратчайший путь, минимальное остовное дерево. Задача коммивояжера – метод ветвей и границ.	2 [2]	0,5 [0,5]
7	Полнота. Теорема Поста.	2 [2]	2 [1]
8	Алгоритмически неразрешимые проблемы.	1 [-]	1 [-]
	ВСЕГО:	20 [12]	12 [8]

Рекомендации по выполнению контрольных работ

Настоящее пособие для студентов-заочников содержит контрольные задания по курсу математической логики и теории алгоритмов и является приложением к учебно-практическому пособию «Математическая логика и теория алгоритмов» авторов Зуева Ю.А. и Садыковой А.Р. для студентов специальности 2202 (230102) всех форм обучения [МГУТУ, 2007].

Предусматривается выполнение одной контрольной работы, содержащей 9 заданий по 10 вариантам. Вариант выбирается в соответствии с последней цифрой номера зачетной книжки.

Контрольная работа должна быть выполнена в отдельной тетради, обложка которой оформляется согласно принятому в МГУТУ образцу (обращаться в деканат).

Решению задачи должно предшествовать условие.

Контрольная работа сдается в деканат.

Контрольная работа

1. С помощью диаграмм Эйлера-Вена показать результаты следующих операций:

1.1. 1.6.

1.2. 1.7.

1.3. 1.8.

1.4. 1.9.

1.5. 1.10.

2. Множество R определяет отношение на множестве 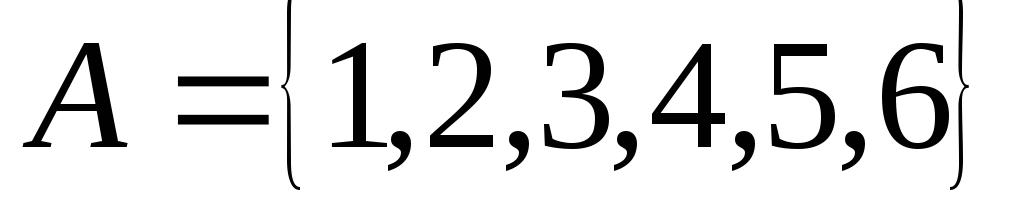. Найдите все упорядоченные пары ему принадлежащие:

2.1. 2.6.

2.2. 2.7.

2.3. 2.8.

2.4. 2.9.

2.5. 2.10.

3. Запишите с помощью кванторов и предикатов следующие утверждения:

3.1. «Яблоки либо сладкие, либо кислые».

3.2. «Некоторые яблоки кислые».

3.3. «Все яблоки кислые».

3.4. «Существуют прилежные и способные студенты».

3.5. «Некоторые студенты ленивые».

3.6. «Все студенты или ленивые или глупые».

3.7. «Некоторые студенты ленивые и глупые».

3.8. «Все студенты ленивые и глупые».

3.9. «Найдется умный и добросовестный студент».

3.10. Все студенты либо умные либо хитрые».

4. Для простых высказываний:

p: «студент сдаст экзамен».

q: «студент выполнит контрольную работу».

составить сложенные высказывания следующих видов:

4.1. 4.6.

4.2. 4.7.

4.3. 4.8.

4.4. 4.9.

4.5. 4.10.

5. Построить таблицу истинности сложного высказывания:

5.1.	5.6.
5.2.	5.7.
5.3.	5.8.
5.4.	5.9.
5.5.	5.10.

6. Доказать, что:

6.1.

6.2.

6.3.

6.4.

6.5.

6.6.

6.7. для

6.8. для

6.9. для

6.10. для

7. Заданы предикаты:

а нравится b больше, чем с.

Используя запишите высказывания

7.1.

7.2.

7.3.

7.4.

7.5.

7.6.

7.7.

7.8.

7.9.

7.10. .

8. Доказать эквивалентности:

8.1.

8.2.

8.3.

8.4.

8.5.

8.6.

8.7.

8.8.

8.9.

8.10.

8. Выяснить, применима ли машина Тьюринга, задаваемая программой П, к слову Р.

9.1

9.2.

9.3.

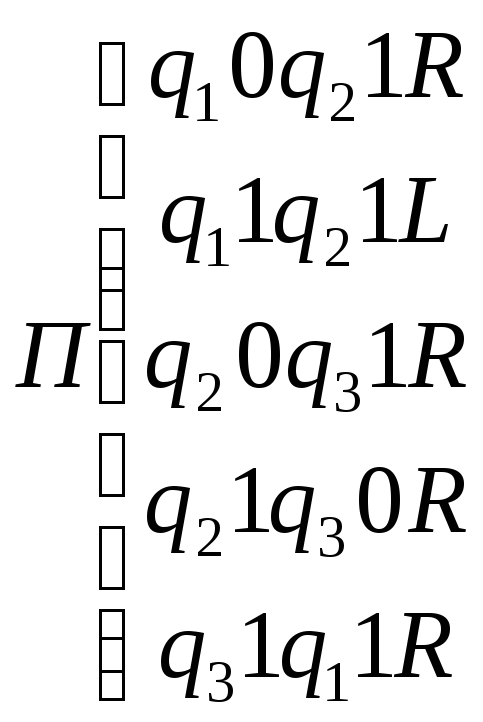
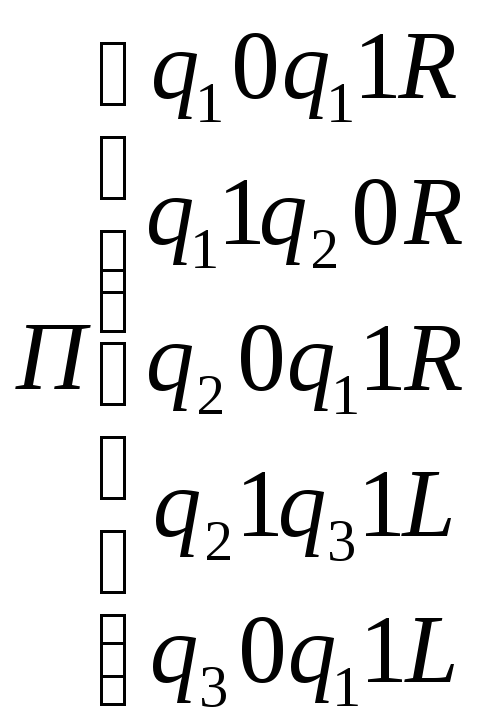
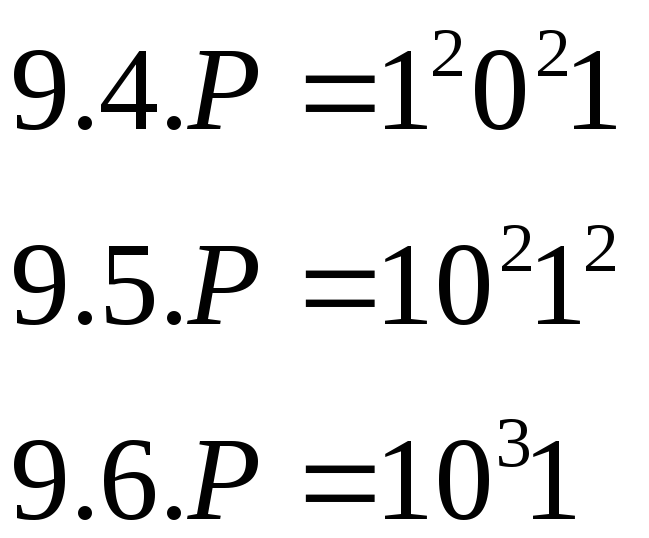
9.4.

9.5.

9.6.

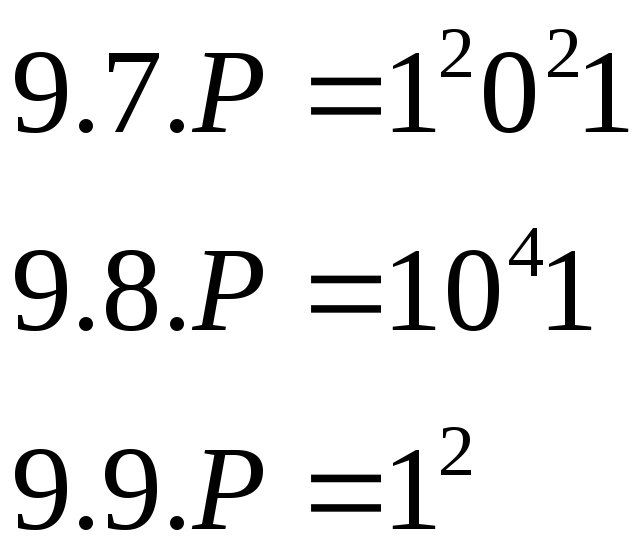
9.7.

9.8.

9.9.

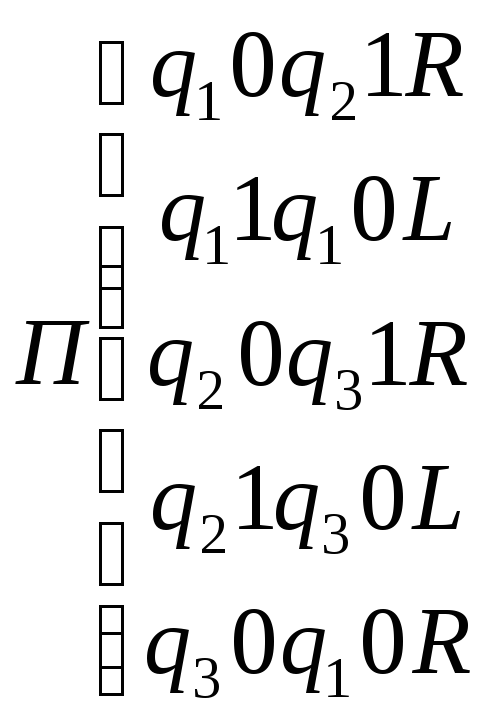
9.10.

Замечание Если в программе отсутствует необходимая команда, то машина Тьюринга остановится, и говорят, что она применима к слову.

Садыкова Альбина Рифовна

Математическая логика

и теория алгоритмов

Рабочая программа и методические указания по выполнению контрольных заданий

Подписано к печати:

Тираж:

Заказ №

8