
Ф едеральное
агентство по образованию
едеральное
агентство по образованию
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
(образован в 1953 году)

Кафедра физики и высшей математики
|
Дистанционное обучение |
|
Физ. мат. 8.11.230102 очн.плн. Физ. мат. 8.11.230102 очн. скр |
А.Р. Садыкова
«Математическая логика
и теория алгоритмов»
Учебно-методические указания практических занятий для студентов специальности 230102 (2202) для дневной формы обучения.

www.msta.ru
5284
Москва – 2005
УДК 519.6
3-93
Садыкова А.Р. Математическая логика и теория алгоритмов. Учебно-методические указания практических занятий для студентов специальности 230102 (2202) для дневной формы обучения. М., МГУТУ, 2005.
В пособии в кратком систематическом виде изложены основные моменты (этапы) проведения практических занятий по дисциплине; примеры заданий предлагаемых для рассмотрения на занятии; примеры вариантов самостоятельных и итоговых работ. Данное пособие поможет преподавателям в проведении практических занятий по дисциплине, в подборе форм и методов работы со студентами.
Авторы: Садыкова Альбина Рифовна.
Рецензент: Д. ф-м. н., профессор Зуев Ю.А.
Редактор: Свешникова Н.И.
Московский государственный университет технологий и управления, 2005
109004, Москва, Земляной вал, 73.
Содержание стр.
Занятие 1 ………………………………………………… 4
Занятие 2 ………………………………………………… 5
Занятие 3 ………………………………………………… 7
Занятие 4 ………………………………………………… 8
Занятие 5 ………………………………………………… 9
Занятие 6 ………………………………………………… 10
Занятие 7 ………………………………………………… 11
Занятие 8 ………………………………………………… 12
-
Общие положения.
Практическое занятие – это одна из форм систематических учебных занятий, на которых обучающиеся приобретают необходимые умения и навыки по тому или иному разделу дисциплины, входящей в состав учебного плана по специальности (направлению) обучения.
-
Основные задачи практических занятий:
- углубление теоретической и практической подготовки обучающихся;
- формирование и развитие способности к творческому мышлению;
- развитие инициативы и самостоятельности обучающихся;
- приближение учебного процесса к реальным условиям работы того или иного специалиста;
- отражение в учебном процессе требований научно-практического прогресса, современных достижений науки и техники.
III. По плану 34 ч. Практических занятий.
Занятие 1. (4 ч.)
Тема: Операции над множествами.
Цель: 1. Выяснить степень усвоения понятия «множества».
2. Научить: 1) способам доказательство тождеств на применение свойств операций над множествами.
2) оформлению доказательств тождеств, с указанием свойств множеств используемых при доказательстве.
План: 1. Математический диктант.
2. Решение задач.
3. Упражнения для домашней работы.
Ход занятия.
-
Математический диктант способствует быстро проверке теоретических знаний студентов. Рекомендуется: 1) рассмотреть 5-10 вопросов; 2) по окончанию провести обзор ответов на поставленные в диктанте вопросы; 3) время проведения не более 30 мин.; 4) проводится письменно на отдельных листочках, которые собираются преподавателем для проверки. Примеры вопросов предлагаемых для математического диктанта:
1) Дайте определение понятия «множества».
2) Приведите пример множества.
3) Закончите предложение: «Два множества А и В считаются равным, если …»
-
Примеры упражнений и задач.
-
Доказать, что если А есть множество корней уравнения
 и
и
 ,
то А=В.
,
то А=В.
-
Доказать, что Ø
 {Ø}.
{Ø}. -
Доказать тождества
а)
![]()
б)
![]()
в)
![]()
Обязательно рассмотреть доказательства как минимум двух тождеств, остальные предложить студентам для самостоятельного рассмотрения.
Пример:
Доказать:
![]() .
.
Доказательство:
Пусть
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
а значит,
,
а значит,
![]() .
Если
.
Если
![]() ,
то имеем
,
то имеем
![]() ,
а значит,
,
а значит,
![]() .
Итак,
.
Итак,
![]() .
Пусть
.
Пусть
![]() .
Если
.
Если
![]() ,
то
,
то
![]() и
и
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
Если
.
Если
![]() ,
то
,
то
![]() и
и
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
Итак,
.
Итак,
![]() .
Итак,
.
Итак,
![]() .
.
-
Примеры заданий предлагаемых для домашней работы.
-
Доказать, что
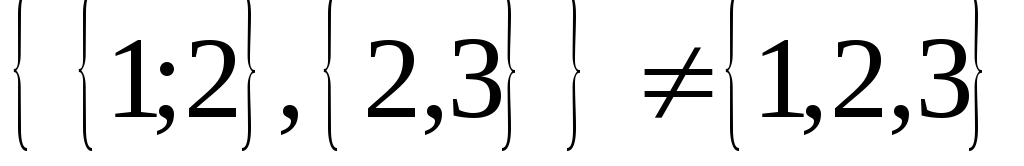 .
. -
Доказать, что существует лишь одно множество, не имеющее элементов.
Занятие 2. (4 ч.)
Тема: Бинарные отношения. Отношения эквивалентности.
Цель: 1) Выяснить степень усвоения понятий «бинарные отношения» и «отношения эквивалентности».
2) Отработать способы записи решения задач.
План: 1) Проверка домашней работы.
2) Решение задач.
3) Домашнее задание.
Ход занятия.
-
Проверить домашнюю работу, разобрав все способы доказательств предлагаемые студентами.
-
Примеры задач:
-
Дано генеалогическое древо (см. рис.). Выпишите упорядоченные пары, находящиеся в следующих отношениях на множестве Р членов этой семьи:
а)
![]()
б)
![]()

-
Множество
 определяет отношение на множестве
определяет отношение на множестве
 .
Найдите все упорядоченные пары, ему
принадлежащие.
.
Найдите все упорядоченные пары, ему
принадлежащие. -
Постройте ориентированный граф отражающий упорядоченные пары, принадлежащие бинарному отношению
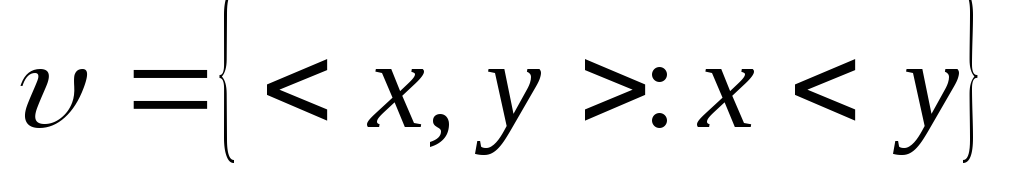 на множествах
на множествах
 и
и
 .
.
Р ешение:
ешение:
-
С помощью таблицы покажите упорядоченные пары бинарного отношения
 на множествах
на множествах
 и
и
 .
.
Решение.

-
Домашняя работа:
-
Диаграмма Хассе частичного порядка R на множестве
 показана на рисунке. Перечислите
элементы R
и найдите минимальный и максимальный
элементы частичного упорядоченного
множества А.
показана на рисунке. Перечислите
элементы R
и найдите минимальный и максимальный
элементы частичного упорядоченного
множества А.

-
Определите, какие из приведённых ниже отношений на Z являются рефлексивными, симметричными, а какие транзитными.
а) «х + у - нечётное»;
б) «х + у - чётное»;
в) «ху - нечётное».
Занятие 3 (4 ч.)
Тема: Алгебра высказываний. Таблицы истинности.
Цель: 1) Выяснить степень усвоения понятий алгебры высказываний.
2) Познакомить с таблицами истинности.
3) Научить пользоваться таблицами истинности для доказательств истинности высказываний.
План: 1) Проверка домашней работ.
2) Решение задач.
3) Самостоятельная работа.
Ход занятия.
-
На доске разобрать задания домашней работы.
-
Примеры задач для рассмотрения.
-
Р: «Логика - забава»,
Q: «Сегодня пятница».
Выразите каждое из следующих составных высказываний в символической форме.
а) Логика – не забава, и сегодня не пятница;
б) Сегодня не пятница, да и логика не забава;
в) Либо логика – забава, либо сегодня пятница.
-
С помощью таблицы истинности показать эквивалентность высказываний
![]() и
и
![]()
|
|
|
|
|
|
|
|
u u л л
|
u л u л |
л л u u |
л u л u |
u л u u |
u л u u |
-
Дан предикат
 :
«х
– целое число и
:
«х
– целое число и
 »
Выразите словами высказывание:
»
Выразите словами высказывание:
 .
. -
Постройте таблицу истинности для следующего высказывания
 .
.
-
Самостоятельная работа проводится как минимум по двум вариантам
Примерный вариант работы может иметь вид:
-
Пусть P, Q и R – высказывания:
P: «Я умираю от жажды»,
Q: «Мой стакан пуст»,
R: «Сейчас три часа».
Запишите, каждое из следующих высказываний:
а) Сейчас три часа и я умираю от жажды.
б) Если я умираю от жажды, то мой стакан пуст.
-
Х – кошка,
 :
«у Х
есть усы»
:
«у Х
есть усы»
Запишите каждое из высказываний в символической форме.
а) усы есть у всех кошек;
б) найдётся кошка без усов.
-
Докажите эквивалентность
![]() ~
~![]() .
.
-
Постройте таблицу истинности
![]() .
.
-
Докажите тождественную истинность
а)
![]()
б)
![]()
Занятие 4 (4 ч.)
Тема: Методы доказательств. Математическая индукция.
Цель: 1) Познакомить с методами доказательства математической индукцией.
2) Научить пользоваться математической индукцией при доказательстве тождеств.
План: 1) Математический диктант.
2) Решение задач.
3) Домашние задания.
Ход занятия.
-
Математический диктант направлен на проверку теоретических знаний по теме «Алгебра высказываний».
Примерные вопросы.
-
Закончите предложение: «Высказыванием называется утверждение, которое …»
-
Дайте определение дизъюнкции.
-
Запишите с помощью кванторов следующее утверждение «Все студенты высокие и умные».
-
Примеры заданий для рассмотрения.
-
Покажите прямым способом, что произведение ху двух нечётных целых чисел х и у всегда нечётно.
Решение:
Т.к. х
и у
нечётные, то
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Получим,
.
Получим,
![]() - нечётное, как сумме чётного числа
- нечётное, как сумме чётного числа
![]() и единицы.
и единицы.
-
Доказать
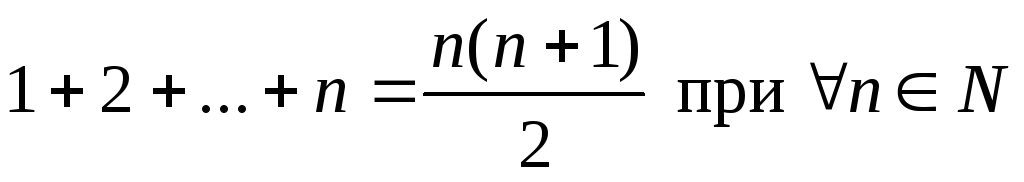 .
.
Доказательство:
Пусть
![]() .
.
При
n=1
получим
![]() ,
т.е.
,
т.е.
![]() верно.
верно.
Предположим,
что при
![]()
![]() - верно.
- верно.
Тогда
при
![]() получим:
получим:
![]()
![]()
![]()
![]() ,
т.е. верно.
,
т.е. верно.
-
 ,
,

-
Домашняя работа.
-
Прямым рассуждением докажите: если n и m – чётные, то n+m – чётное.
-
Доказать методом математической индукции
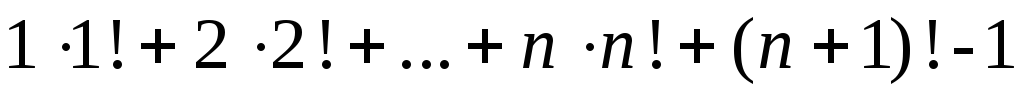 ,
,
 .
.
Занятие 5 (4 ч.)
Тема: Булева алгебра. Булевы функции.
Цель: 1) Выяснить степень усвоения законов булевой алгебры.
2) Познакомить студентов с картами Карно, как способом получения Д.Н.Ф.
План: 1) Проверка домашнего задания..
2) Решение задач.
3) Самостоятельная работа (15 мин).
4) Домашняя работа.
Ход занятия.
-
Разобрать домашнее задание на доске.
-
Примеры заданий для рассмотрения.
-
Доказать закон дистрибутивности.
Доказательство: Воспользуемся таблицами истинности.
![]()
|
|
|
|
|
|
|
|
|
|
u u u u л л л л |
u u л л u u л л
|
u л u л u л u л |
u u u л u u u л |
u u u л л л л л |
u u л л л л л л
|
u л u л л л л л
|
u u u л л л л л |
-
Упростить
 с помощью карты Карно.
с помощью карты Карно. -
Упростить булеву функцию:
 .
.
-
Самостоятельная работа проводится как минимум по двум вариантам.
Вариант заданий может иметь вид:
-
Привести к Д.Н.Ф.
![]()
-
Привести к К.Н.Ф.
![]()
-
Домашняя работа.
-
Найти Д.Н.Ф. и К.Н.Ф. булева выражения
 .
. -
Изобразить карту Карно булева выражения с Д.Н.Ф.
![]() и найдите его
упрощенную версию.
и найдите его
упрощенную версию.
Занятие 6 (4 ч.)
Тема: Группы. Кольца. Поля.
Цель: Выяснить степень усвоения понятий: группы, кольца, поля.
План: 1) Проверка домашнего задания.
2) Математический диктант (20 мин.)
3) Решение задач.
4) Домашняя работа.
Ход занятия.
-
На доске разобрать домашнюю работу.
-
Математический диктант направлен на усвоение понятий: группы, кольца, поля. Результаты разобрать по окончанию диктанта.
Примеры вопросов диктанта:
-
Дайте определение полугруппы.
-
Какой элемент называют единичным.
-
Дайте определение кольца.
-
Доказать, что
 не группа.
не группа.
-
Примеры заданий для рассмотрения.
-
Ассоциативна ли операция
 на множестве М,
если:
на множестве М,
если:
а)
![]() ,
,
б)
![]() ,
,
в)
![]() .
.
-
Какие из указанных числовых множеств с операциями являются группами:
а)
![]() ,
где А – одно из множеств N,
Z,
Q.
,
где А – одно из множеств N,
Z,
Q.
б)
![]() ,
,
![]()
-
Какие из следующих числовых множеств образуют кольцо относительно обычных операций сложения и умножения:
а)
Z;
б)
![]() ;
в) Q.
;
в) Q.
-
Домашняя работа.
Доказать:
а)
![]() - группа.
- группа.
б)
![]() - не группа.
- не группа.
Занятие 7 (4 ч.)
Тема: Графы. Задача коммивояжера.
Цель: Выяснить степень усвоения понятия: «граф».
План: 1) Проверка домашнего задания.
2) Математический диктант (20 мин.)
3) Решение задач.
4) Домашняя работа.
Ход занятия.
-
Разобрать на доске домашнее задание.
-
Математический диктант. Примеры вопросов:
-
Дайте определение Эйлерова графа.
-
Как (и чем) определяется простой граф?
-
Приведите пример цикла длины 5.
-
Дан граф

Приведите пример маршрута длины 4 в данном графе.
-
Примеры заданий для рассмотрения.
-
Постройте граф
 с множеством вершин
с множеством вершин
 и множеством рёбер
и множеством рёбер
 .
. -
Найдите циклы: а) два длины 5;
 б)
три длины 4;
б)
три длины 4;
в) два длины 3, в граф G.
-
К
 оммивояжер
должен совершить поездку по городам
вернуться обратно, побывав в каждом
городе ровно один раз, сведя при этом
затраты на передвижение к минимуму.
Решите эту задачу, если её геометрическая
модель имеет вид:
оммивояжер
должен совершить поездку по городам
вернуться обратно, побывав в каждом
городе ровно один раз, сведя при этом
затраты на передвижение к минимуму.
Решите эту задачу, если её геометрическая
модель имеет вид:
-
Домашняя работа.
Изобразите
орграф с вершинами
![]() и матрицей смежности
и матрицей смежности

Занятие 8 (4 ч.)
Тема: Итоговое занятие.
Цель: Выяснить степень усвоения понятий математической логики и теории алгоритмов.
План: 1) Решение индивидуальных заданий.
2) Отчёт преподавателю результатов решения индивидуальных занятий.
Ход занятия.
-
Вариант заданий может иметь вид:




