3. Комплексные числа в полярных координатах

Применим полярные координаты (r,φ) на комплексной плоскости z (рис.1). Неотрицательное число r называется модулем или абсолютной величиной комплексного числа z. Из рис.1 видно, что применяя формулы теоремы чемпиона Олимпийских игр по кулачному бою, Пифагора с острова Самос, легко получить .

Ясно, что r по модулю всегда больше или равен нулю, причём r = 0 лишь в том случае, когда z = 0. Отметим, что для модулей двух комплексных чисел z₁ и z₂ естественным образом выполняется неравенство Минковского. Действительно, если z₁ = х₁ + iу₁ и z₂ = x₂ +iy₂, тоили

Это становится очевидно, если вспомнить про геометрический смысл |z₁|, |z₂| и |z₁ + z₂|.

Угол φ обычно называют аргументом, реже фазой комплексного числа и пишут φ = Arg z. При z ≠ 0 аргумент определяется по формулам (см. рис.1)

cos  = , sin  = , (1)

но согласно правилам тригонометрии, с точностью до 2πк (к− целое) то есть является действительной многозначной функцией. Обычно используется главное значение аргумента arg z, удовлетворяющее неравенствам –π φ ≤π в этом случае у каждого числа z существует лишь один аргумент.

В случае z = 0 аргумент не определён и может считаться любым. Если вспомнить из школьного курса тригонометрии формулу для тангенса половинного угла, то используя (1), можно записать

tg = = = ,  .

Стало быть, для главного значения аргумента

arctg z = 2 arc tg ,

что является верным для всех комплексных чисел, кроме действительных, отрицательных и нуля.

Применение полярных координат позволяет получить тригонометрическую (иногда её называют «полярной») форму комплексного числа. Для этого нужно вместо х и у в определение комплексного числа подставить их выражения из (1). Получим

z = r(cos φ + i sin φ).

Любое действительное число А может быть представлено в виде комплексного (тригонометрическая форма) следующим образом.

A = (2)

Пример:

2 = 2(cos 0 + i sin 0) или

-17 = 17(cos π + i sin π).

Пример: Запишем число z = (-8) в тригонометрической форме: ,.

.

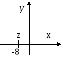
Т.к. z находится в левой полуплоскости, то . Тригонометрическая форма этого числа имеет вид:.

Пример: Запишем число в алгебраической форме. Модульz = 2, а аргумент .

Его действительная часть , а мнимая часть. Таким образом, алгебраическая форма числаz имеет вид .

Пример:

1) Вычислить модуль числа 3+4i

Re (3+4i)=3; Im(3+4i)=4; r =

2) Найти главное значение аргумента числа 3-4i

argz = 2 arctg

3) Записать комплексное число 1 в тригонометрической форме.

1 = 1(cos0 + isin0)

Задачи

1. Записать в тригонометрической форме числа 3+4i, -1+2i, -,

2. Найдите модуль комплексных чисел 3i, 3, 1, i.

3. Запишите числа ив тригонометрической форме

Тест

1. Что такое φ?

а) одна из фаз трёхфазного электродвигателя,

б) Фаза или аргумент комплексного числа,

в) угол между радиус-векторам комплексного числа и осью OY.

2. У чисел имеет и

а) аргументы будут равными,

б) модули будут равными,

в) модули будут равными, а аргументы нулевыми,

г) и аргументы и модули будут равными

3. У комплексного числа

а) ReZ = ImZ,

б) r=1,

в) φ=.

4. Сложение и вычитание комплексных чисел

Операции сложения и вычитания комплексных чисел ничем не отличаются от правил сложения и вычитания алгебры, изучаемой в школе. Единственное о чём нужно помнить, действительная и мнимая части должны быть записаны отдельно и перед мнимой частью должен стоять i (в общем случае результатом является комплексное число!). Сложение определяется следующим образом

z₁ +z₂ = (х₁ + iy₁) + (x₂ + iy₂) = (x₁ + x₂) + i(y₁ + y₂)

Пример

+ i =

Вычитание вводится как разность z₁ и z₂, то есть z₁ – z₂ = (x₁ + iy₁) – (x₂ + iy₂) = (x₁ – x₂) + i(y₁ – y₂).

Пример

+= +

Примечания:

1. Вспомните как складываются и вычитаются векторы по своим координатам и убедитесь в существовании прямой аналогии с содержанием этого раздела.

2. Результатом сложения двух комплексных сопряжённых чисел всегда является действительное число, результатом их вычитания - чисто мнимое. Убедитесь в этом.

Задачи

1. Сложить а) 2+3i и 2-3i, б) 2+3i и -2-3i, в) 2+3i и -2+3i

2. Вычесть а) 2+3i из 2-3i, б) 2+3i из -2-3i, в) 2+3i из -2+3i

Тест

1. Можно ли комплексные числа связать с векторами ?

а) Можно, б) Нельзя, в) В некоторых случаях нельзя.

2. Результат сложения иявляется

а) действительным числом, б)число мнимым числом, в)нулём.

3. Результатом вычитания иявляется

а) действительное число, б) число мнимое число, в)нуль.

4. Какой аргумент имеет результаты вычитания двух равных чисел?

а) 0, б) , в), г), д), е) любой.

5. Умножение комплексных чисел и возведение их в степень

Операция умножения проводится по правилам умножения многочленов с учётом правила возведения в степень мнимой единицы i.

Ясно, что

и т.д.

Закономерность установить не сложно.

(3)

где n- любое натуральное число.

Перемножим два комплексных числаи.

= .

Пример:

Примечание: Результатом умножения комплексного числа на его сопряжение является действительное число. Убедитесь в этом сами.

Более эффектно операция умножения выглядит, когда перемножаются комплексные числа, заданные в тригонометрической форме:

= r₁(cosφ₁ + i sinφ₁) и z₂ = r₂(cosφ₂ + i sinφ₂) z = z₁z₂ = r₁(cosφ₁ + i sinφ₁) ∙ r₂(cosφ₂ + i sinφ₂) = r₁r₂ [(cosφ₁cosφ₂ – sinφ₁sinφ₂) + i (sinφ₁cosφ₂ + sinφ₂cosφ₁)].

Вспоминая школьный курс тригонометрии (теоремы сложения для косинуса и синуса) получим z = z₁z₂ = r₁r₂ [cos(φ₁ + φ₂) + i sin(φ₁ + φ₂)].

Таким образом, получаем правило «при умножении двух комплексных чисел друг на друга их модули перемножаются, а аргументы складываются».

Это свойство распространяется на любое число сомножителей. Нужно только либо перемножать их последовательно, либо пользоваться «таблицей умножения» (3). Геометрически результирующая картина будет следующая. Вектор Ополучается из вектора О, поворотом последнего на угол φ₂ (против движения часовой стрелки, если φ₂ › 0 ) и удалением в r₂ раз. Из введения правил умножения легко получается очень красивая формула Муавра, позволяющая возводить любое комплексное число в любую натуральную степень n. Пусть Тогда из вышеизложенного в данном разделе следует, что

, то есть

(4)

Равенство (4) называется формулой Муавра и часто используется на практике, Сам Абрахам Муавр установил не только правило возведения в степень, но и научился извлекать корень любой степени из комплексного числа. При этом правила он формулировал словесно, а аналитическую запись предложил позднее Леонард Эйлер.