!Оптика и квантовая механика / Лекции / Прочие лекции / Лекции по квантовой механике / LEC4

Глава 3. Волновые свойства частиц.

§ 1. Гипотеза де-Бройля.

В 1924 г Луи де-Бройль выдвинул смелую гипотезу: частицы вещества наряду с корпускулярными свойствами имеют также волновые. Перенес на частицы вещества те же правила перехода от одной картины к другой, как в случае света.

Фотон обладает энергией и импульсом:

По идее де –Бройля движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна ,

Одним из проявлений волновых свойств частиц, не имеющих ана­лога в ньютоновой механике, является дифракция. В 1927 г. Дэвиссон и Джермер в США и Дж. П. Томсон в Англии независимо друг от друга подтвердили гипотезу де Бройля, показав, что электроны тоже испы­тывают дифракцию при отражении от кристаллов с соответствующим расположением атомов. Мы рассмотрим эксперимент Дэвиссона и Джермера, так как его интерпретация наиболее проста.

Дэвиссон и Джермер исследовали отражение электронов от твер­дых тел с помощью установки, схематически изображенной на рис.1.

В этой установке можно было изменять энергию электронов в первич­ном пучке, угол их падения на мишень и положение детектора. Согласно классической физике рассеянные электроны вылетают во всех направлениях, причем интенсивность этих электронов мало зависит от угла рассеяния и еще меньше — от энергии первичных электронов. Работая с блоком никеля в качестве мишени, Дэвиссон и Джермер под-твердили эти предсказания классической физики.

Однажды в их установку случайно попал воздух и окислил поверхность металла. Чтобы удалить окисную пленку и очистить никель, мишень отожгли в высокотемпературной печи. После этой обработки ее поставили обратно и возобновили измерения. Но те­перь результаты сильно отличались от тех, которые наблюдались до происшествия. Вместо монотонного изменения интенсивно­сти рассеянных электронов от угла наблю­дались ярко выраженные максимумы и минимумы, положение которых зависело от энергии электронов! На рис.2 показаны типичные графики распределения интенсив­ности электронов (в полярных координа­тах), полученные после происшествия; на этих графиках интенсивность электронов при любом угле рассеяния пропорциональ­на расстоянию от точки рассеяния до кри­вой при рассматриваемом угле.

Сразу же возникают два вопроса: чем объясняется этот новый эффект и почему он не наблюдался до отжига мишени из никеля?

Используя гипотезу де Бройля, можно предположить, что электрон­ные волны испытывают дифракцию на мишени так же, как и рентге­новские лучи испытывают дифракцию при брэгговском отражении от плоскостей в кристалле. Это объяснение стало еще более правдопо­добным, когда обнаружилось, что нагревание блока никеля до высокой температуры приводит к образованию одного крупного кристалла из большого количества отдельных маленьких кристаллов, обычно образу­ющих блок. При этом все атомы крупного кристалла занимают места в регулярной решетке.

Давайте посмотрим, можно ли доказать, что открытие Дэвиссона и Джермера обусловлено волнами де Бройля. В одном из опытов пучок электронов с энергией 54 эв падал перпендикулярно поверхности никелевой мишени, и в распределении интенсивности рассеянных элек­тронов наблюдался ярко выраженный максимум под углом 50° к на­правлению первичного пучка. Углы падения и рассеяния пучка элек­тронов относительно системы плоскостей Брэгга одинаковы и равны 65°, как это показано на рис.3.

Рас­стояние между плоскостями в этой системе, измеренное с помощью рентгеновских лучей, равно 0,91 . Уравнение Брэгга, описывающее по­ложение максимумов в дифракцион­ной картине, имеет вид n=2asin.

Здесь а = 0,91 -постоянная кристаллической решетки и =65°. Примем n=1, тогда дебройлевская длина волны рассеянных электронов будет равна = 20,91 sin 65° = 1,65 .

Теперь воспользуемся формулой де Бройля =h/mv для вычисле­ния предполагаемой длины волны электронов. Кинетическая энергия электронов 54 эв мала по сравнению с его массой покоя , равной 5,1 эв, поэтому релятивистскими эффектами можно пренебречь. Так как , импульс электрона равен , откуда длина волны электрона равна

,

что отлично согласуется с длинной волны, наблюдаемой на опыте.

Таким образом, опыт Дэвиссона-Джермера является прямым подтверждением гипотезы де Бройля о волновой природе движущихся тел.

§ 2. Волны де Бройля и принцип неопределенности

Частоту волны v можно измерить, сосчитав число гребней и впа­дин волн, проходящих мимо наблюдателя за определенный интер­вал времени, т. е.

здесь N - число гребней,- время, за которое проводятся изме­рения. Однако следует иметь в виду, что эта формула строго спра­ведлива только для чисто синусоидальной волны, амплитуда кото­рой сохраняется постоянной. Эта волна должна обладать единст­венной частотой, так как в противном случае можно пропустить колебания, соответствующие биениям. Такая ситуация (волна с определенной частотой) не встречается в физике, поскольку реаль­ные волны возникают и в некоторый момент времени прекращают свое существование; отсюда в соответствии с гармоническим анали­зом следует, что в волне должны присутствовать и другие частоты. Чтобы понять, как это влияет на наше представление о свойствах цуга физических волн, рассмотрим простейший случай. Пусть волна состоит из двух компонент с очень близкими частотами. Тогда за время наблюдения может произойти биение и один из гребней (или впадин) будет пропущен рис.4. Тaким образом, мы видим, что измеренное нами число гребней имеет некоторую неопределенность, которая зависит от того, сколько гребней пропущено за время измерения. Отсюда следует, что неопределенность измеренной частоты запи­шется в виде

.

Увеличивая продолжительность наблюдения, эту неопределенность можно уменьшить, но всегда будет выполняться соотношение .

Данное соотношение можно получить более изящным способом, если представить цуг волн конечной длины в виде интеграла Фурье, но главный результат останется тем же. Чем больше продолжитель­ность измерения частоты, тем точнее ее можно измерить. (Строгий гармонический анализ дает в 4 раз меньшую неопределенность, поскольку в этом случае мы можем выполнить более точные изме­рения, чем с помощью подсчета гребней. В дальнейшем нашем рас­смотрении будет учитываться множитель 4) Записанное выше соотношение должно выполняться также для световой волны, т. е. для фотона. Следовательно, записывая условие

и используя равенство E=hv, приходим к выводу, что должна существовать неопределенность энергии ,

связанная с продолжительностью измерения энергии фотона. Таким образом, мы имеем

(1)

Это неравенство можно переписать также в виде, более удобном для случая частиц:

.

Первый множитель (заключенный в круглые скобки) представляет собой неопределенность (неточность) импульса фотона, а второй — неопределенность (неточность) его координаты. Таким обра­зом, мы имеем

(2)

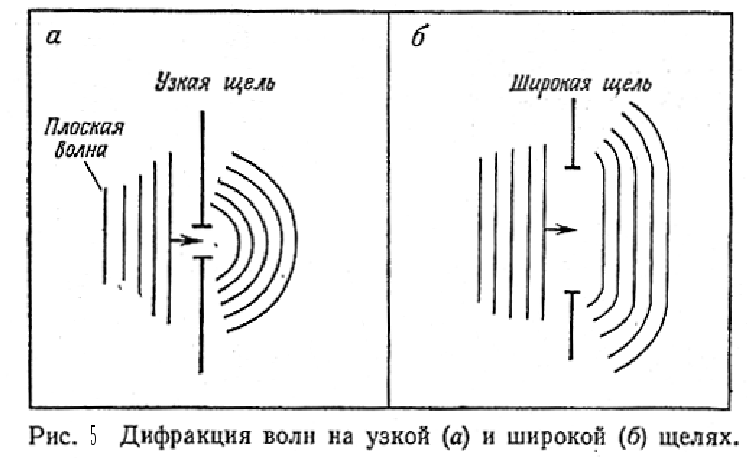где р — составляющая импульса р вдоль оси х, в чем мы могли бы убедиться, если бы проделали соответствующие выкладки. Это соотношение между неопределенностями (1) и (2) называется принципом неопреде­ленности Гейзенберга. Мы воспользовались фотоном для формулировки основного свойства волновых цугов конечной длины на языке частиц. Рассмотрим физический смысл этого свойства. Начнем с классической картины дифракции волн.

Если пропустить через щель световой пучок (рис.5), то на экране получится либо размытое (дифрагированное) световое пятно, когда ширина щели сравнима с длиной волны, либо точное изобра­жение щели, когда ширина щели много больше длины световой вол­ны. Используя понятие импульса фотона p=h/=, это явление можно интерпретировать уже не с волновой точки зрения, а с точки зрения потока частиц, т. е. фотонов. Если фотоны пролетают через щель, то их положение в щели известно с неопределенностью .

Следовательно, х-составляющую импульса фотонов нельзя опре­делить с точностью, превышающей. Чем шире щель, тем точнее будет определен импульс фотонов и тем меньше размы­вается световой пучок; чем уже щель, тем меньше точность опреде­ления импульса и тем больше размытие пучка.

Оба аспекта — как волновой, так и. корпускулярный — дают один и тот же результат. Волновая картина дает нам распределение интенсивности волны на экране в зависимости от отношения шири­ны щели к длине волны, в то время как корпускулярная картина приводит нас к понятию относительной вероятности того, что фотон попадает в данную область экрана, которая зависит от ширины щели и неопределенности в величине импульса. Таким образом, интенсивность волны играет ту же роль, что и распределение вероятности.

Принимая гипотезу де Бройля о волновых свойствах частиц, мы приходим к заключению, что для случая прохождения через щель электронов мы получили бы те же самые соотношения.

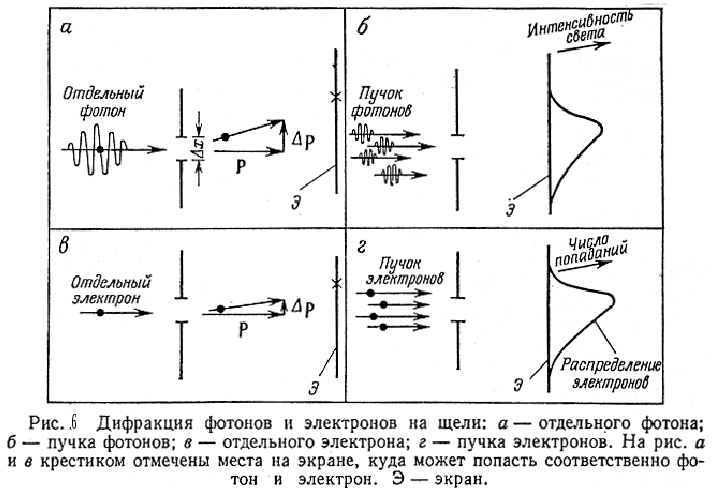
Как показано на рис.6, после прохождения электронами щели шириной: разброс их поперечной составляющей импульса удов­летворяет соотношению. Это означает, что нельзя точно предсказать место на экране, в которое попадет отдельный электрон. Можно указатъ лишь относительную вероятность попадания элект­ронов в ту или иную область экрана.

Когда через щель проходит большое число электронов, на экране получается распределение, аналогичное распределению интенсив­ности света. Для отдельного электрона (или любой другой частицы) это распределение будет представлять собой вероятность попадания в данную область экрана. Как и распределение интенсивности света, распределение вероятности зависит от длины волны электрона. Вероятность нахождения частицы в данной точке пространства-времени определяется волновой природой материи.

Волновые свойства света можно характеризовать амплитудой, а также интенсивностью, представляющей собой квадрат амплитуды. Когда же речь идет о волнах, отвечающих частицам, то заранее совсем неясно, с какой из этих величин мы имеем дело. Рассмотрим это на примере интерференционной картины от двух щелей (рис.7).

Если волна характеризует вероятность обнаружить частицу и, следовательно, является аналогом интенсивности света, то распреде­ление от двух щелей будет представлять собой на экране сумму рас­пределений, даваемых каждой из щелей в отдельности, и никогда не будет взаимного гашения двух волн. С другой стороны, если волна представляет собой амплитуду вероятности (т. е. для получения вероятности найти частицу в данной точке амплитуду волны следует возвести в квадрат), то может происходить взаимное гашение двух волн, приводящее в отличие от предыдущего случая к появлению нулей в распределении вероятности.

Если провести такой эксперимент для частиц (электронов), то обнаружится, что взаимное гашение действительно происходит. Следовательно, волна представляет собой амплитуду вероятности. Таким образом, из гипотезы де Бройля следует, что частицы характеризуются волной, квадрат амплитуды которой выданной точке пространства-времени дает вероятность найти частицу в этом месте. Иными словами, все частицы описываются волновой функцией, причем величина дает вероятность того, что в момент времени t частица находится окрестности dx точки x. Вся информа­ция, которую мы можем иметь о частице, содержится в амплитуде соответствующей волны.