ЛАБОРАТОРНЫЕ ПО ФИЗИКЕ 4 семестр / LR_7_3

Лабораторная работа 7.3

Изучение явления интерференции света

от двух когерентных источников в опыте Юнга.

Библиографический список

1. Савельев И.В. Курс общей физики. – М.: Наука, 1978, т. 2.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1985.

Цель работы: определение расстояния между щелями по интерференционной картине в схеме опыта Юнга.

Приборы и оборудование: лазер, тест-объект, экран, оптическая скамья.

Описание метода и экспериментальной установки.

О дним из первых ученых, кто наблюдал явление интерференции был Томас Юнг, который в 1802 году получил интерференционную картину, в установке, показанной на рис. 1.

Свет, предварительно прошедший через светофильтр, проходя через отверстие S в экране A падал на экран В, в котором были проделаны две тонкие щели S₁ и S₂. Эти щели являлись когерентными источниками света и давали достаточно четкую картину интерференции на экране.

В настоящей лабораторной работе вместо обычного источника света со светофильтром для повышения степени когерентности используется гелий-неоновый лазер. Схема установки приведена на рис. 2.

S ₁ и S₂ – источники когерентного излучения, s₁ и s₂ – пути света от источников до точки наблюдения Р, d – расстояние между щелями, L – расстояние между экранами В и С,  -оптическая разность хода лучей.

Разность фаз колебаний, возбужденных волнами, приходящими в точку Р от источников S₁ и S₂ равна:

, (1)

где показатель преломления среды, ₀ – длина волны света в вакууме.

Отсюда следует, что если в оптической разности хода укладывается целое число длин волн , то разность фаз оказывается кратной 2, и в этой точке будет наблюдаться интерференционный максимум.

Если в оптической разности хода укладывается полуцелое число длин волн , то в этой точке будет наблюдаться интерференционный минимум.

Из рис. 2 видно что:

. (2)

Учитывая, что , получаем:

. (3)

Так как и , то из уравнения (3) следует, что оптическая разность хода равна:

. (4)

Подставим в выражение (4) условия наблюдения максимума и минимума интерференции, соответственно получим:

, (5)

. (6)

Ширина интерференционной полосы на экране (расстояние между соседними минимумами интенсивности) будет определяться соотношением:

, (7)

где - длина волны в среде, заполняющей пространство между источниками света и экраном.

Описание лабораторной установки

Установка (рис. 3) смонтирована на оптической скамье 4. Источником света служит полупроводниковый лазер 1. Параллельный световой пучок освещает тест-объект 2, который представляет собой тонкий стеклянный диск с непрозрачным покрытием, на котором по кругу нанесены пары щелей с разными расстояниями между ними. Пары щелей равной ширины объединены в группы по четыре. В пределах групп изменяются расстояния между щелями. Свет лазера, проходя через пару щелей, падает на экран 3, на котором и проводятся измерения ширины инт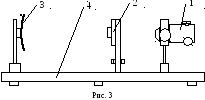 ерференционной полосы (х).

Порядок выполнения работы

1. Добиться четкого изображения интерференционных полос.

2. Провести пять измерений ширины интерференционных полос для каждой из пар щелей. Полученные данные усреднить. Данные занести в таблицу 1, где 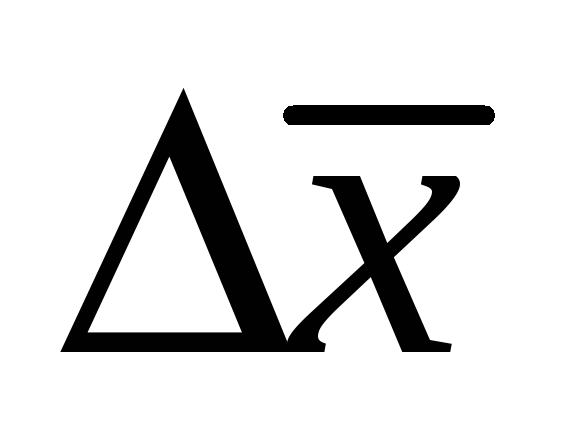- усредненное значение ширины интерференционной полосы.

Таблица 1.

№ изм.	xi, мм
	1 пара щелей	2 пара щелей	3 пара щелей	4 пара щелей
1
2
3
4
5

3. Измерить с помощью линейки расстояние L между экраном и тест-объектом и записать его в лабораторном журнале

4. По результатам измерений, зная длину волны излучения лазера ( = 632,8 нм) рассчитать расстояние между щелями по формуле:

Получится по одному значению d для каждой пары щелей из группы. Полученные результаты занести в таблицу 2.

Таблица 2.

№ пары щелей	1	2	3	4
, м

3. Рассчитать погрешности измерений.

4. Окончательный результат записать в виде:

.

Контрольные вопросы

1. Что такое интерференция?

2. При каком условии можно наблюдать интерференционную картину?

3. Что такое «полосы равной толщины» и «полосы равного наклона»?

4. Для опыта Юнга (интерференция от двух щелей) указать положение первого максимума и записать условие следующего максимума через длину волны, расстояние от экрана до щели L и расстояние между щелями d (в опыте Юнга d<<L).

5. В опыте Юнга вначале берется свет с длиной волны λ₁ = 600 нм, а затем λ_2. Какова длина волны во втором случае, если 7-я светлая полоса в первом случае совпадает с 10-й темной во втором?

6. На пути одного из интерферирующих лучей помещается стеклянная пластинка толщиной 12 мкм. Определить, на сколько полос сместится интерференционная картина, если показатель преломления стекла n = 1,5; длина волны света λ = 750 нм и свет падает на пластинку нормально.

21