Лекция9

Уравнение Гельмгольца

Принцип максимума для уравнения .

Теорема. Решение уравнения , определённое и непрерывное в замкнутой области, не может достигать во внутренних точках области положительных максимальных и отрицательных минимальных значений

Доказательство.

Пусть , тогда ,,откуда

Но в этом случае в правой части уравнения стоит отрицательное число, т.е. ур-е не выполнено. Это предположение показывает, что исходное уравнение не верно.

Фундаментальное решение.

Трёхмерный случай.

Ситуация сложнее

,,и любое из этих решений можно взять как фундаментальное.

Двумерный случай

, ,

В ограниченной области можно брать любое в неограниченной выбор фундаментального решения определён выбором условия на бесконечности.

Для вывода третьей формулы Грина для оператора Гельмгольца необходимо провести те же, выкладки, что и для оператора Лапласа.

Таким образом сразу получаем интегральное представление

Краевые задачи

Внутренняя задача Дирихле для уравнения

Теорема. Задача Дирихле не может иметь более одного классического решения.

Доказательство.

В силу линейности достаточно доказать, что

имеет только тривиальное решение. Но в силу принципа максимума , и , т.е

.

Задача Неймана и третья краевая задача.

Теорема. При на краевая задача не может иметь более одного классического решения.

Доказательство. Достаточно показать, что однородная задача имеет только тривиальное решение

Воспользуемся первой формулой Грина.

Т.к.

Примечание. Если знак будет другим, то однородная задача может иметь и нетривиальные решения.

Краевые задачи для уравнения

Внутренние краевые задачи могут иметь неединственное решение, если совпадёт с собственным значение для оператора Лапласа для этой области. В этом случае решения неоднородной задачи может вообще не быть либо оно будет определяться неоднозначно.

Функция Грина.

Рассмотрим следующую задачу Дирихле

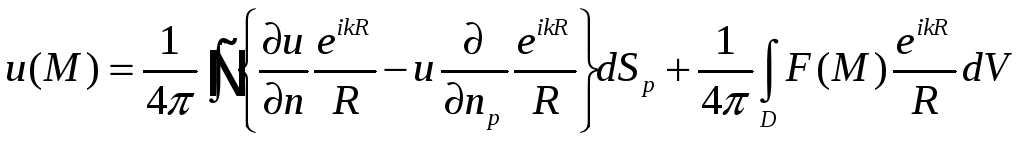
Пусть решение

Применяя к и вторую формулу Грина.

Складывая и обозначая

Выберем функцию так, чтобы

Внешние задачи

Для выделения единственного решения для уравнения

Нужно потребовать равномерное стремление к нулю.