Лекция 9 основные сведения о развертках поверхностей

В начертательной геометрии поверхность рассматривают как гибкую, нерастяжимую пленку не имеющую толщины. Отдельные поверхности, если их некоторым образом деформировать, можно совместить с одной плоскостью без разрывов и складок. Такие поверхности относятся к развертываемым поверхностям.

Фигуру, полученную при совмещении развертываемой поверхности с плоскостью, называют разверткой.

Поверхности, которые невозможно совместить с плоскостью относятся к неразвертываемым поверхностям.

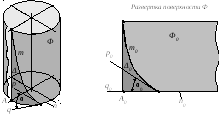
Рис. 63

Между поверхностью и ее разверткой существует взаимно однозначное соответствие, выражающееся в следующих свойствах (рис. 63):

1. Точке А поверхности Ф соответствует единственная точка А₀ на ее развертке Ф₀.

2. Кривой m поверхности Ф соответствует кривая m₀ на ее развертке Ф_0, причем длины кривых равны между собой. Если на поверхности задана геодезическая линия, то на развертке ей соответствует прямая.

3. Угол α между касательными р и q к кривым m и n поверхности Ф соответствует равный ему угол α₀ на развертке Ф_0.

4. Площади SучасткаΔповерхности на поверхностиФ₀соответствует равная ей площадьS₀участкаΔ₀на разверткеФ₀.

Все перечисленные свойства доказывают в дифференциальной геометрии. Там же доказывается, что развертываемыми поверхностями являются торсы (поверхности, образованные касательными к пространственной кривой), в частности, цилиндрические и конические поверхности [ 1 ]. Остальные кривые поверхности относятся к неразвертываемым поверхностям.

К развертываемым поверхностям относятся так же все многогранные поверхности, так как их грани являются плоскостями, которые естественно возможно совместить с одной плоскостью. Развертка многогранника представляет собой плоскую фигуру, составленную из его граней.

Развертки развертываемых поверхностей

В начертательной геометрии развертки строят графически, т. е. с помощью чертежных инструментов. При этом развертки многогранных поверхностей можно построить точно, если не учитывать графическую погрешность.

Развертки кривых развертываемых поверхностей строят приближенно, заменяя при этом кривую поверхность соответствующей многогранной поверхностью, развертку которой и принимают за приближенную развертку кривой поверхности. Цилиндрические и конические поверхности при построении развертки на комплексном чертеже заменяют соответственно поверхностями призм и пирамид.

Однако развертки кривых развертываемых поверхностей так же считают точными, так как любая точка поверхности может быть точно построена на ее развертке.

Построение разверток поверхностей пирамид и конусов с доступной вершиной

Построение разверток поверхностей пирамид сводится к нахождению натуральных величин треугольных граней.

Для построения развертки конической поверхности ее заменяют поверхностью вписанной пирамиды.

На рис. 64, а и б приведен пример построения приближенной развертки участка конической поверхности, для чего в нее вписана поверхность пирамиды, состоящая из четырех треугольных граней SAB, SBC, SCD и SDE. Величины ребер пирамиды SA, SB, SC, SD и SE определены способом вращения, а величины сторон основания AB, BC, CD и DE по условию задачи равны их горизонтальным проекциям, т. е. AB =A₁B₁, BC = B₁C₁, CD = C₁D₁ и DE = D₁E₁.

Построение развертки выполняют в любом месте чертежа, так как изображение развертки не имеет проекционной зависимости с комплексным чертежом конической поверхности (рис. 64, б).

Развертка поверхности вписанной пирамиды является приближенной разверткой заданной конической поверхности.

Рис. 64

Отличие в графическом оформлении разверток поверхностей пирамид и конусов состоит в том, что на развертке поверхности пирамиды основание представляет собой ломанную линию с прямолинейными звеньями, а у развертки конической поверхности кривую линию (см. рис. 64, б).