Лекции 1-9 / Лекция 1

Лекция 1

ЦЕЛЬ, СРЕДСТВО И МЕТОД НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Начертательная геометрия изучает пространственные формы реальных объектов и отношения между ними с помощью их изображений на плоскости, полученных проекционным методом.

В начертательной геометрии любой объект рассматривается, как совокупность геометрических фигур его ограничивающих, называемых в общем случае: точка, линия и поверхность. Например, геометрическое тело − прямой круговой конус ограничен конической (боковая поверхность) и плоской (основание) поверхностями, которые пересекаются по кривой линии – окружности, а вершиной является точка.

Основными геометрическими фигурами , с помощью которых изучаются объекты в начертательной геометрии, чаще всего выступают простейшие точка, прямая и плоскость, вследствие простоты их графических изображений. Кроме того, они являются фигурами, ограничивающими большинство реальных объектов. Например, параллелепипед (крышка стола, спичечный коробок и др.) ограничен шестью плоскими поверхностями (гранями), пересекающимися попарно по двенадцати прямым линиям (ребрам), которые в свою очередь определенным образом пересекаются в точках – вершинах восьми углов параллелепипеда.

Под точкой в начертательной геометрии понимают не материальную частицу, а место в пространстве, не имеющее никакого измерения. Иначе говоря, точка – нуль мерная геометрическая фигура. Изображают ее условно для визуального восприятия в виде маленького кружочка и обозначают прописными буквами латинского алфавита (A, B, C, D и др.) или арабскими цифрами (рис. 1, а).

Линия представляется в виде траектории движущейся точки, в результате чего образуется одномерная геометрическая фигура, т.е. имеющая одно измерение – протяженность. Обозначают линию в начертательной геометрии строчными буквами латинского алфавита (a, b, c, d, f, h, l, m, n, p, q и др.) (рис. 1, б).

Поверхность в общем случае можно определить непрерывно движущейся линией, называемой образующей. Построенная таким образом геометрическая фигура не имеет третьего измерения - толщины, т. е. является двумерной. Обозначают поверхность в начертательной геометрии прописными буквами греческого алфавита (       и др.) (рис. 1, в).

Рис. 1

Точка линия и поверхность находятся между собой в определенных отношениях, основными из которых являются их взаимная принадлежность и взаимное пересечение.

Можно сказать, что любая геометрическая фигура состоит из точек. В состав фигуры также могут входить линии и поверхности. Все это характеризует понятие взаимная принадлежность.

Две линии и линия с поверхностью пересекаются в точке, а поверхности пересекаются по линии. Представление об этих геометрических операциях формирует понятие пересечение.

В тех случаях, когда необходимо передать информацию о форме геометрической фигуры, прибегают к ее графическому вычерчиванию.

Изображение геометрической фигуры пространства на плоскости, выполненное по установленным стандартами правилам, называют чертежом, который является основным инструментом изучения ее пространственных форм. Поэтому к чертежу предъявляют ряд требований. Сформулируем основные из них:

1. Чертеж должен быть обратимым, что позволяет установить по нему форму и размеры объекта пространства;

2. Чертеж должен быть простым, что оценивается числом графических операций, необходимых для его выполнения с помощью чертежных инструментов. Чем таких построений меньше, тем проще чертеж;

3. Чертеж должен быть наглядным, что можно оценить скоростью восприятия пространственных форм изображенного объекта. Чем быстрее это восприятие, тем нагляднее чертеж.

Чертеж в начертательной геометрии получают проекционным методом, сущность которого сводится к следующему алгоритму:

• в пространстве задается плоскость чертежа, называемая плоскостью проекций, относительно которой формируется положение изображаемой геометрической фигуры;

• через точки фигуры проводятся проецирующие прямые (лучи);

• строятся точки пересечения проецирующих прямых с плоскостью проекций.

Различают центральное и параллельное проецирование 1, 2. В первом случае проецирующие прямые исходят из некоторой точки пространства – центра проецирования. Во втором проецирующие прямые параллельны. В частности они могут быть перпендикулярны плоскости проекций. В этом варианте принято говорить – перпендикулярное или ортогональное проецирование, а в остальных случаях параллельного проецирования – косоугольное.

Механизм получения чертежа с помощью параллельного проецирования, как основного метода, используемого в начертательной геометрии, показан на рис. 2, где

s – направление проецирования

ABC – объект пространства – плоскость;

' – плоскость проекций;

A'B'C' – параллельная проекция (чертеж) плоскости ABC;

l, p и q – проецирующие прямые (l || p || q || s), проходящие соответственно через точки A, B и C.

Отметим некоторые свойства параллельного проецирования (см. рис. 2):

1. Проекцией точки является точка, так как проецирующая прямая пересекает плоскость проекций в точке. Например, прямая l пересекает плоскостью проекций  ' в одной единственной точке A'.

2. Проекция линии или поверхности есть плоская фигура. Для прямой в общем случае проекцией является прямая, так как, она является результатом пересечения двух плоскостей, например, A'B' – прямая пересечения плоскости, образованной параллельными прямыми l и p, с плоскостью проекций  '.

3. Если в пространстве точка принадлежит линии, то ее

проекция принадлежит проекции линии. Например, E принадлежит BC, следовательно, E' принадлежит B'C'.

4. Проекции параллельных прямых параллельны. Например, если EF || AC, то E'F' || A'C'.

5. Отношение отрезков одной прямой равно отношению проекций этих отрезков. Например, AF : FB = A'F' : F'B'.

6. Если линии в пространстве пересекаются, то их соответствующие проекции пересекаются в точке, являющейся проекцией точки пересечения линий. Например, AB пересекает BC в точке B (в символьной форме AB ∩ BC = B), следовательно, A'B' ∩ B'C' = B' (см. рис. 2).

Доказательства последних четырех свойств следует провести самостоятельно, используя знания элементарной геометрии.

C

E

B

A

F

C'

A'

П'

F'

E'

B'

s

p

l

q

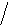
Рис. 2

Чертеж плоскости АВС, представленный на рис. 2, является необратимым, так как по одной проекции невозможно реконструировать заданный объект, т. е. восстановить его размеры и форму. Например, A' B' C' может являться проекцией любого треугольника, вершины которого расположены на проецирующих прямых l, p и q.

Рассмотрим более подробно способ получения обратимого чертежа, предложенный французским геометром Г. Монжем (1746 – 1818).

ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ НА ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИПРОЕКЦИЙ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ

Сущность данного способа получения обратимого чертежа состоит в ортогональном проецировании заданного объекта на две взаимно-перпендикулярные плоскости проекций, что позволяет по двум проекциям восстановить его форму и размеры.

На рис. 3, а представлена пространственная модель простейшей геометрической фигуры – точки, ортогональные проекции которой построены на двух взаимно-перпендикулярных плоскостях проекций, где:

Π₁ – горизонтальная плоскость проекций;

Π₂ – фронтальная плоскость проекций;

x₁₂ – ось проекций;

A – заданная геометрическая фигура – точка;

A₁ – горизонтальная проекция точки A;

A₂ – фронтальная проекция точки A;

p и l – проецирующие прямые, перпендикулярные соответственно плоскостям проекций Π₁ и Π₂.

Отрезки A₁A₁₂ и A₂A₁₂, связывающие проекции A₁ и A₂ точки A, перпендикулярны оси проекций x₁₂. Действительно, если p  Π₁, то p  x₁₂. Следовательно, A₂A₁₂  x₁₂, так как p || A₂A_12. Аналогично можно доказать, что A₁A₁₂  x_12.

Величины отрезков A₁A₁₂ и A₂A₁₂ равны расстояниям от точки A до плоскостей проекций соответственно Π₂ и Π₁ (см. рис. 3, а), так как AA₂ || Π₁ и AA₁ || Π₂, что вытекает из геометрических закономерностей данного способа проецирования.

Плоскости проекций, пересекаясь между собой, делят пространство на четыре части, называемые четвертями или квадрантами, которые принято нумеровать так, как показано на рис. 3, а. Каждая часть пространства ограничена двумя полуплоскостями, которые называют для плоскости проекций Π₁ – передняя и задняя, а для плоскости Π₂ – верхняя и нижняя. Рассматриваемый объект может теоретически быть помещен в любую часть пространства, в отличие от «наблюдателя», который всегда находится в первой четверти.

Рис. 3

Построенная таким образом пространственная модель с практической точки зрения неудобна, вследствие ее громоздкости и искажения форм и размеров проецируемого объекта.

Г. Монж предложил преобразовать эту модель в плоскую совмещением плоскостей проекций в одну плоскость, где присутствуют только изображения проецируемого объекта. Такое преобразование принято осуществлять поворотом горизонтальной плоскости проекций Π₁ вокруг оси x₁₂, как показано стрелками на рис. 3, а, до совмещения ее с неподвижной фронтальной плоскостью проекций Π₂.

На рис. 3, б представлена плоская модель пространства, с изображенными на ней проекциями A₁ и A₂ заданной точки A. Такую модель называют комплексным чертежом (или эпюром) проецируемой геометрической фигуры – точки A. Прямую, соединяющую проекции A₁ и A₂ называют линией связи.

Комплексный чертеж является обратимым, достаточно простым и практически ненаглядным. В большинстве случаях отсутствие наглядности компенсируется наличием пространственного воображения, т. е. свойством человеческого сознания воспроизводить пространственный образ объекта по его проекциям.

В инженерной практике часто возникает необходимость построения чертежа (детали, сборочной единицы и др.), состоящего из трех и более проекционных изображений. Механизм образования комплексного чертежа в этом случае точно такой же, как и для двух плоскостей проекций.

На рис. 4, а представлена пространственная модель, состоящая из трех взаимно-перпендикулярных плоскостей проекций – горизонтальной (Π₁), фронтальной (Π₂) и профильной (Π₃). Очевидно, что эти плоскости образуют три пары взаимно-перпендикулярных плоскостей проекций - Π₁  Π₂, Π₁  Π₃ и Π₂  Π_{3 .}

Рис. 4

Плоскости Π₁ и Π₂ пересекаются с профильной плоскостью Π₃ по осям проекций, обозначать которые принято соответственно y₁₃ и z₂₃ . Геометрические закономерности в системах Π₁  Π₃ и Π₂  Π₃ такие же, как и в системе Π₁  Π₂.

Комплексный чертеж в данном случае образуется совмещением плоскостей Π₁ и Π₃ с фронтальной плоскостью проекций Π₂ вращением их вокруг соответствующих осей проекций (x₁₂ и z₂₃), как показано стрелками на рис. 4, а.

Построение профильной проекции (A₃) точки A показано на пространственной модели (см. рис. 4, а) в системе плоскостей проекций Π₂  Π₃ и комплексном чертеже (рис. 4, б).

Другой путь построения проекции A₃ точки A возможен через систему плоскостей проекций Π₁  Π₃, что менее рационально вследствие «раздвоения» оси проекций y₁₃ при образовании комплексного чертежа и как следствие разрыв линии связи проекций A₁ и A₃ , что видно на рис. 4, б.

В конструкторской практике часто возникает ситуация, когда необходимо иметь связь между графическими и аналитическими моделями геометрических фигур. В этом случае декартову систему координат объединяют с пространственной моделью (рис. 5, а), что позволяет легко строить на комплексном чертеже геометрические фигуры, заданные аналитически.

Построение проекций А₁, А₂ и А₃ точки A по ее координатам (x_A, y_A, z_A) показано на рис. 5, б.

Рис. 5

Безосный комплексный чертеж

Чертеж, выполненный на основе комплексного чертежа без нанесения осей проекций, называют безосным. Отсутствие осей не нарушает проекционных связей и не оказывает влияния на изображения.

На рис. 6, а показан безосный комплексный чертеж точек A и B, положение которых относительно плоскостей проекций Π₁ и Π₂ не зафиксировано. При этом на чертеже, возможно, определить только взаимную координацию точек, т. е. разность их одноименных координат (y_A – y_B и z_A – z_B) или соответствующих расстояний от плоскостей проекций заданной системы Π₁  Π₂. Причем таких систем плоскостей проекций может быть бесчисленное множество, оси проекций которых расположены в биссекторных плоскостях углов координатного трехгранника.

В начертательной геометрии при изучении отдельных тем и решении задач появляется необходимость в наличии конкретной системы плоскостей проекций для заданной на безосном чертеже геометрической фигуры. Эту систему фиксируют проведением соответствующей оси проекций, перпендикулярно линиям связи, в любом удобном для решения задачи месте (рис. 6, б).

Рис. 6

Вопросы для самопроверки

1. Сформулируйте определение точки исходя из понятий линия и поверхность?

2. Каким образом пространственная модель из трех взаимно перпендикулярных плоскостей проекций преобразуется в плоскую?

3. Отметьте преимущества безосного комплексного чертежа?

6