Лекции 1-9 / Лекция 7

Лекция 7

Пересечение многогранных и кривых поверхностей

Многогранные поверхности пересекаются между собой в общем случае по пространственной ломаной линии, звенья которой отрезки прямой. Эта линия при определенных условиях может распадаться на части. Вершинами ее являются точки пересечения ребер одной многогранной поверхности с гранями другой и наоборот ребер второй с гранями первой. Сторонами линии пересечения являются отрезки прямых, по которым пересекаются грани обеих поверхностей. Построение такой линии, как и в случае с плоскими сечениями многогранников, сводится к задачам по построению пересечения прямой с плоскостью и плоскостей соответственно при нахождении вершин и отрезков этой линии.

Рис. 49

На рис. 49, а показаны две призмы, поверхности которых пересекаются по пространственной ломаной линии, вершины которой обозначены A, B, C, и D. Точки A и B являются точками пресечения ребра нижней призмы с двумя гранями верхней, а точки С и D определяются в пересечении ребра верхней призмы с гранями нижней. Наглядное изображение нижней призмы, с построенной на ней линией пересечения, представлено на рис. 49, б.

Кривая и многогранная поверхности пересекаются между собой в общем случае по пространственной ломаной, звенья которой плоские кривые линии. Эта линия при определенных условиях может так же распадаться на части. Вершинами ее являются точки пересечения ребер многогранника с кривой поверхностью, а звенья представляют собой плоские кривые линии, полученные в результат пересечения граней многогранника с кривой поверхностью. Поэтому построение линии пересечения рассматриваемых поверхностей сводится к двум простым задачам, а именно, к пересечению поверхности с прямой и плоскостью.

Рис. 50

На рис. 50, а представлен комплексный чертеж, на котором показано пересечение цилиндрической поверхности вращения с поверхностью треугольной призмы. В этом примере грани призмы пересекают поверхность цилиндра по эллипсам. Наглядное изображение цилиндрической поверхности вместе с линией пересечения, на которой обозначены характерные точки А, В и С, представлено на рис. 50, б.

Кривые поверхности пересекаются между собой по пространственной кривой линии, которая при определенных условиях может распадаться на части, как и в предыдущих комбинациях пересекающихся поверхностей.

Комплексный чертеж пересекающихся цилиндрических поверхностей вращения приведен на рис. 51, а. Линия их пересечения представляет собой пространственную кривую линию четвертого порядка. На рис. 51, б представлено наглядное изображение нижнего цилиндра вместе с линией пересечения, на которой обозначены характерные точки А, В, С и D.

Рис. 51

Распадение линии пересечения поверхностей на части во всех рассмотренных комбинациях при ее построении происходит в том случае, если одна поверхность полностью охватывает другую. Такое пересечение образно называют «прострелом». В остальных комбинациях называют – «врезом» (см. рис. 49, 50, и 51). Границей двух таких вариантов взаимного расположения поверхностей является их касание друг друга.

Некоторые особые случаи пересечения поверхностей

1. Поверхности цилиндров (призм) с параллельными образующими (ребрами) и конусов и пирамид с общей вершиной пересекаются по прямым.

На рис. 52, а приведен пример пересечения на наглядном чертеже поверхностей двух цилиндров по образующим l и p, а на рис. 52, б поверхностей пирамиды и конуса по прямым SA и SB. Очевидность этих случаев пересечения не требует доказательства.

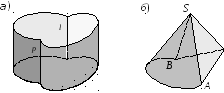
Рис. 52

2. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекутся и еще по одной плоской кривой второго порядка.

На рис. 53, а приведен пример пересечения на комплексном чертеже (показана только фронтальная проекция) поверхностей эллиптического конуса с круговым основанием и сферы по двум окружностям p и l.

3. Если две поверхности второго порядка описаны около третьей поверхности второго порядка (или вписаны в нее), то они пересекаются между собой по двум кривым второго порядка (рис. 53, б). Это положение известно под названием теорема Монжа.

На рис. 53, б показан пример на комплексном чертеже, где пересекаются цилиндрическая и коническая поверхности вращения по двум эллипсам. В этом случае обе поверхности касательные к общей сфере.

Рис. 53

Следует отметить, что плоскости симметрии Σ (Ο, q) и Γ(i ∩ j) в примерах, приведенных на рис. 53, а и б, параллельны фронтальной плоскости проекций.

Доказательства второго и третьего особых случаев пересечения поверхностей рекомендуется посмотреть в курсах аналитической геометрии [2].

4. Соосные поверхности вращения (т. е. поверхности с общей осью) пересекаются по окружностям (рис. 54, а и б).

Действительно при вращении образующих p, l и q вокруг оси i каждая их точка, например, А и В, осуществляет движение по окружности. То же самое происходит и с точками Е и F, находящимися в пересечении образующих поверхностей. Траектории вращения этих точек представляют собой линии пересечения рассматриваемых поверхностей (рис. 54, а).

Рис. 54

В примерах приведенных на рис. 54, а и б даны лишь фронтальные проекции. Причем оси поверхностей вращения i и j расположены параллельно плоскости проекций П₂, вследствие чего окружности, получаемые при пересечении заданных поверхностей, изображаются на эту плоскость проекций в виде прямых.

За ось сферы (см. рис. 54, б) можно принять любой ее диаметр. Поэтому сфера соосна одновременно с конической (ось i) и цилиндрической поверхностями (ось j).

Применение сферических посредников для построения линии пересечения

поверхностей

Сферические посредники рационально использовать в том случае, если пересекающиеся поверхности имеют общую плоскость симметрии, и каждая из них несет на себе семейство окружностей, по которым их могут пересечь концентрические или эксцентрические сферы общие для обеих поверхностей.

Для реализации на комплексном чертеже этого положения необходимо при этом, чтобы общая плоскость симметрии пересекающихся фигур была параллельна какой-либо плоскости проекций.

Из поверхностей, имеющих семейство (одно и более) окружностей, отметим поверхности вращения и эллиптические поверхности, которые наиболее часто встречаются в практике. Для построения линии пересечения таких поверхностей используют, как отмечалось ранее, концентрические или эксцентрические сферические посредники, выбор которых связан с конкретным видом заданных геометрических фигур и их взаимным расположением.

Концентрические сферические посредники можно использовать только в том случае, если пересекаются поверхности вращения, оси которых также пересекаются. Это связано с тем, что центр вспомогательных сфер должен лежать одновременно на осях обеих поверхностей, т. е. в точке их пересечения, так как только в этом случае сферы будут соосны с заданными поверхностями и пересекут их по окружностям.

На рис. 55, а показана на комплексном чертеже фронтальная проекция пересекающихся цилиндрической и конической поверхностей вращения, общая плоскость (i ∩ j) симметрии которых параллельна плоскости Π₂. Следовательно, фронтальные очерки заданных поверхностей, расположенных в этой плоскости, пересекутся. Точки их пересечения, проекции которых обозначены на чертеже буквами А₂ и В₂, являются наиболее удаленными относительно горизонтальной плоскости проекций. Расстояние от точки (О) пересечения осей до точки А (или В) в данной задаче определяет радиус максимальной сферы R_max, необходимой для решения задачи.

Рис. 55

В общем случае радиус максимальной сферы (R_max) определяют по чертежу величиной расстояния от точки пересечения осей поверхностей вращения до наиболее удаленной точки в пересечении очерков.

Сфера минимального радиуса (R_min) должна быть касательная к одной поверхности, а другую пересекать, так как любая сфера, радиус которой меньше R_min, не пересечет одну из поверхностей и поэтому не сможет служить в качестве посредника.

С помощью сферы минимального радиуса определяем точки C и D наиболее приближенные к горизонтальной плоскости проекций, для чего строим линии пересечения (окружности) этой сферы с цилиндрической и конической поверхностями. По отношению к цилиндрической поверхности окружность образуется в результате касания сферы минимального радиуса и цилиндрической поверхности.

Плоскости построенных окружностей перпендикулярны соответствующим осям заданных поверхностей и изображаются на фронтальную плоскость проекций в виде отрезков прямых вследствие того, что общая плоскость симметрии (i ∩ j) параллельна фронтальной плоскости проекций.

В итоге вспомогательная сфера минимального радиуса включает в себя две окружности, пересекающиеся между собой в двух точках C и D (см. рис. 55, а).

Для построения случайных точек следует использовать сферы, радиусы которых расположены в интервале между R_min и R_max. В качестве примера на рис 55, а построены точки 1, 2 и 3, 4.

Рассмотрим еще один пример (рис. 55, б), где пересекаются цилиндрическая поверхность вращения с осью j и поверхность эллиптического конуса, основание которого окружность, отмеченная знаком . Очевидно, что сечения поверхности эллиптического конуса плоскостями, параллельными основанию, будут окружности, множеством центров которых является прямая q.

Ось цилиндра j и прямая q, пересекаясь между собой, определяют плоскость симметрии, расположенную параллельно фронтальной плоскости проекций.

Исходные условия в приведенном примере позволяют сделать вывод о возможности применения сферических посредников для построения линии пересечения заданных поверхностей.

Наиболее удаленные от горизонтальной плоскости проекций точки А и В находятся в общей плоскости симметрии пересекающихся поверхностей и, следовательно, в пересечении фронтальных очерков. Построение наиболее приближенных к Π₁ точек С и D показано на комплексном чертеже (см. рис. 55, б).

Рассмотрим последовательность построения случайных точек в данном примере:

1. Пересекаем коническую поверхность плоскостью Γ¹ по окружности радиуса r¹ с центром в точке К¹. Плоскость Γ¹ расположена в интервале между экстремальными точками А, В и С, D.

2. Из точки К¹ проводим перпендикуляр к плоскости Γ¹ до пересечения его с осью цилиндра (точка О¹⁾. Этот перпендикуляр является множеством центров сфер, которые могут включать в себя заданную на конической поверхности окружность радиусом r¹.

3. Строим вспомогательную сферу радиусом R¹ с центром в точке О¹, включающую в себя заданную на конической поверхности окружность плоскостью Γ¹. Следовательно, эта сфера, соосная с цилиндрической поверхностью, содержит в себе окружность на конусе.

4. Определяем две окружности в пересечении вспомогательной сферы с цилиндрической поверхностью вращения. Они изображаются на плоскость Π₂ в виде прямолинейных отрезков, перпендикулярных оси цилиндра.

5. Находим точки пересечения (1, 2 и 3, 4) построенных окружностей на цилиндрической поверхности с окружностью, заданной на конусе.

Для построения других случайных точек следует повторить указанную последовательность для новой окружности на конической поверхности и так далее. При этом центры вспомогательных сфер каждый раз будут находиться в разных местах оси цилиндра. Такие сферы в этом случае называю эксцентрическими.

В заключении следует подчеркнуть, что использование сферических посредников позволяет строить линии пересечения поверхностей указанного класса используя только одну проекцию. Это важно с практической точки зрения, так как в конструкторской работе поверхности вращения чаще всего изображают одной проекцией.

Вопросы для самопроверки

1. В каком случае поверхности треугольных призм пересекутся по двум треугольникам?

2. Как построить вершины линии пересечения многогранных поверхностей?

3. Назовите плоские линии, которые могут получиться в пересечении граней треугольной призмы с конической поверхностью вращения, если ребра призмы параллельны оси?

4. Что собой представляет в общем случае линия пересечения поверхностей второго порядка?

5. В каком случае кривые и многогранные поверхности пересекаются по прямым линиям?

6. Когда поверхности вращения пересекаются по окружностям?

7. Могут ли поверхности вращения пересекаться по гиперболам и параболам?

8. Назовите условия использования сферических посредников для построения линии пересечения поверхностей?

9. Как определить максимальный и минимальный радиусы сферического посредника для построения линии пересечения поверхностей вращения с пересекающимися осями?

10. Какие преимущества имеют сферические посредники по сравнению с плоскими при построении линии пересечения поверхностей при прочих равных условиях?

6