Лекция 5

Принцип построения общих элементов пересекающихся геометрических фигур

Общие элементы (точка или линия) получаются в результате пересечения:

• линий;

• линии с поверхностью;

• поверхностей.

В первых двух случаях общим элементом пересекающихся фигур является точка, а в третьем линия, которая графически определяется дискретным рядом ее точек. Поэтому задачи на построение точки пересечения линии с поверхностью и линии пересечения поверхностей следует свести к рассмотренной ранее задаче о пересечении линий. При этом отмечалось, что необходимым условием пересечения линий является их принадлежность одной поверхности. На основании этого сформулируем принцип построения общих элементов пересекающихся геометрических фигур.

Сущность принципа состоит в ведении вспомогательных (дополнительных) поверхностей для получения в них пересекающихся линий. Такие вспомогательные поверхности в начертательной геометрии образно называют «посредниками», построенные линии в которых должны принадлежать пересекающимся геометрическим фигурам.

Алгоритм нахождения точки пересечения линии с поверхностью выглядит следующим образом (рис. 34, а):

1) через заданную линию проводим вспомогательную поверхность (посредник) –Φ  l;

2) строим линию пересечения посредника с заданной поверхностью – p = Φ ∩ Σ;

3) находим точку пересечения построенной линии с заданной – К = p ∩ l.

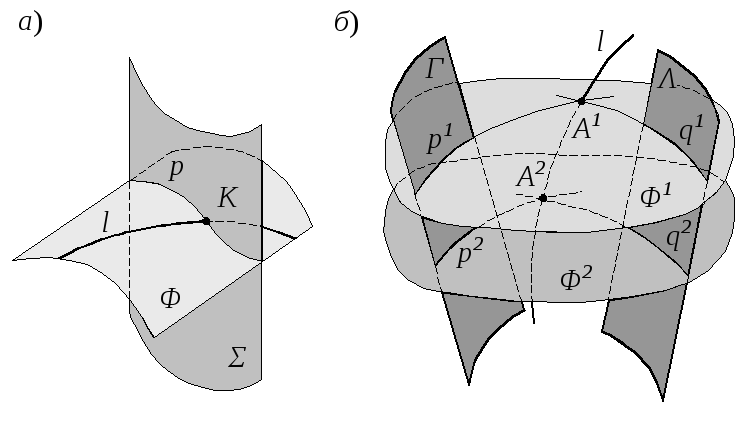
Рис. 34

Построенная точка К является результатом пересечения линий p и l, лежащих в одной вспомогательной поверхности Φ. Тем самым выполнено необходимое условие пересечения линий.

Алгоритм построения точки А¹, принадлежащей линии пересечения (l) поверхностей Γ и Λ выглядит следующим образом (рис. 34, б):

1) пересекаем поверхности Γ и Λ вспомогательной поверхностью (посредником) –Φ¹;

2) строим линии пересечения посредника с заданными поверхностями – p¹ = Φ¹ ∩ Γ, q ¹ = Φ¹ ∩ Λ;

3) определяем точку пересечения построенных линий – А¹ = p¹ ∩ q ¹.

Для нахождения точки А² линии пересечения алгоритм построения следует повторить еще раз с другим посредником (Φ²) и так далее для каждой последующей точки.

Вспомогательную поверхность, если это возможно, выбирают таким образом, чтобы в пересечении ее с заданными поверхностями получались простейшие линии (прямые, окружности), которые в свою очередь изображались бы на плоскости проекций в виде простейших. Поэтому выбор посредника зависит от:

• вида пересекающихся геометрических фигур;

• их взаимного расположения;

• положения геометрических фигур относительно плоскостей проекций.

Чаще всего в качестве посредника выступают плоскости, цилиндрические и сферические поверхности.

Пересечение прямой с плоскостью

Построение точки пересечения прямой с плоскостью проведем в соответствии с рассмотренным алгоритмом на пересечение линии с поверхностью.

В качестве посредника, включающего в себя заданную прямую l, следует взять плоскость (Φ) (рис. 35). Причем для решения задачи на комплексном чертеже эта плоскость обязательно должна быть частного положения. Последнее условие необходимо потому, что во втором пункте алгоритма потребуется решать более сложную задачу на пересечение плоскостей. В случае плоскости частного положения для ее решения не потребуется дополнительных построений, так как одна проекция (Е₂F₂) линии пересечения плоскостей (Φ и Σ) задана.

Алгоритм построения точки пересечения прямой с плоскостью выглядит следующим образом (см. рис. 35):

1) через заданную прямую проводим вспомогательную фронтально проецирующую плоскость – Φ  l, Φ  П₂;

2) строим прямую пересечения посредника с заданной плоскостью – Φ ∩ Σ = EF (E = m ∩ Φ, F = n ∩ Φ);

3) определяем точку пересечения построенной прямой с заданной – K = EF ∩ l.

Рис. 35